7.2. Статистическое оценивание

Пусть из генеральной совокупности извлекается выборка объема n, причем значение признаках₁ наблюдаетсяm₁ раз,х₂m₂ раз,...,х_k наблюдаетсяm_k раз,- объем выборки.

Мы можем сопоставить каждому значению x_i относительную частотуm_i/n.

Статистическим распределением выборки называют перечень возможных значений признака x_i и соответствующих ему частот или относительных частот (частостей) m_i (w_i).

Числовые характеристики генеральной совокупности, как правило неизвестные, (средняя, дисперсия и др.) называют параметрами генеральной совокупности (обозначают, например,или, ). Доля единиц, обладающих тем или иным признаком в генеральной совокупности, называется генеральной долей и обозначаетсяр.

По данным выборки рассчитывают числовые характеристики, которые называют статистиками (обозначают , или ,, выборочная доля обозначаетсяw). Статистики, получаемые по различным выборкам, как правило, отличаются друг от друга. Поэтому статистика, полученная из выборки, является толькооценкойнеизвестного параметра генеральной совокупности.Оценка параметра - определенная числовая характеристика, полученная из выборки. Когда оценка определяется одним числом, ее называютточечной оценкой.

В качестве точечных оценок параметров генеральной совокупности используются соответствующие выборочные характеристики. Теоретическое обоснование возможности использования этих выборочных оценок для суждений о характеристиках и свойствах генеральной совокупности дают закон больших чисел и центральная предельная теорема Ляпунова.

Выборочная средняя является точечной оценкой генеральной средней, т.е. _≈

Генеральная дисперсия имеет 2 точечные оценки: -выборочная дисперсия;- исправленная выборочная дисперсия³. -исчисляется при, а - при. Причем в математической статистике доказывается, что

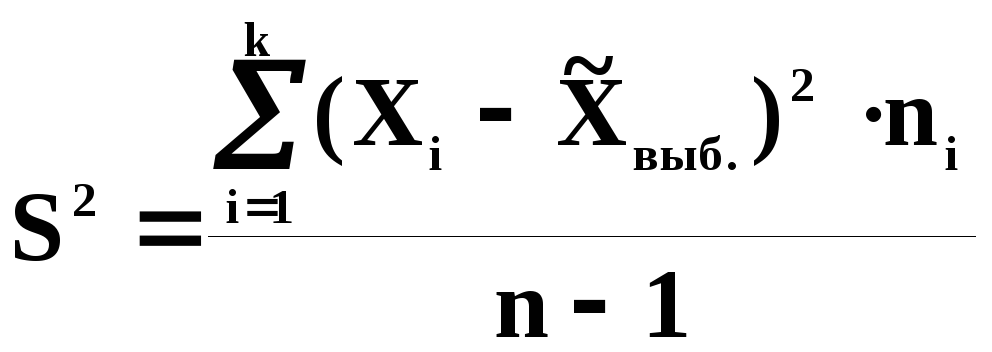или (7.1)

При больших объемах выборки ипрактически совпадают.

Генеральное среднее квадратическое отклонение так же имеет 2 точечные оценки:- выборочное среднее квадратическое отклонение и- исправленное выборочное среднее квадратическое отклонение.используется для оцениванияпри, адля оценивания, при_;при этом, а.

7.3. Ошибки выборки

Поскольку выборочная совокупность представляет собой лишь часть генеральной совокупности, то вполне естественно, что выборочные характеристики не будут точно совпадать с соответствующими генеральными. Ошибка репрезентативности может быть представлена как разность между генеральными и выборочными характеристиками изучаемой совокупности:, либо.

Применительно к выборочному методу из теоремы Чебышева следует, что с вероятностью сколь угодно близкой к единице можно утверждать, что при достаточно большом объеме выборки и ограниченной дисперсии генеральной совокупности разность между выборочной средней и генеральной средней будет сколь угодно мала.

(7.2)

где -средняя по совокупности выбранных единиц,

- средняя по генеральной совокупности,

- среднее квадратическое отклонение в генеральной совокупности.

Запись показывает, что о величине расхождения между параметром и статистикой , можно судить лишь с определенной вероятностью, от которой зависит величина t.

Формула (7.2) устанавливает связь между пределом ошибки , гарантируемым с некоторой вероятностью Р, величиной t и средней ошибкой выборки.

Cогласно центральной предельной теореме Ляпунова выборочные распределения статистик (при n ³30) будут иметь нормальное распределение независимо от того, какое распределение имеет генеральная совокупность. Следовательно:

(7.3)

где Ф₀(t) - функция Лапласа.

Значения вероятностей, соответствующие различным t, содержатся в специальных таблицах: при n ³30 - в таблице значений Ф₀(t), а при n < 30 в таблице распределенияt-Стьюдента. Неизвестное значениепри расчете ошибки выборки заменяется

В зависимости от способа отбора средняя ошибка выборки определяется по разному:

Таблица 7.1