
Міністерство транспорту та зв’язку України
Українська державна академія залізничного транспорту
Факультет “Управління процесами перевезень”
Кафедра “Управління експлуатаційною роботою”
ОСНОВИ ТЕОРІЙ СИСТЕМ І УПРАВЛІННЯ
частина І
Методичні вказівки по виконанню контрольної роботи з дисципліни „Основи теорій систем і управління” для студентів напряму 1004 – Транспортні технології: спеціальності 100403 “Організація перевезень та управління на транспорті (залізничний транспорт)” та слухачів ІППК
Харків 2007
Методичні вказівки розглянуто і рекомендовано до друку на засіданні кафедри „Управління експлуатаційною роботою” “__”___________ 200__ р., протокол №____.
Рекомендовано для студентів спеціальності 100403 ОПУТ (залізничний транспорт) безвідривної форми навчання та слухачів ІППК.
Укладачі: професор Т.В. Бутько,
асистент В.В. Петрушов,
асистент В.М. Прохоров
Рецензент
доцент А.О. Поляков
Зміст
стор.
Вступ ………………………………………………………………………...4
1 Побудова системи за заданими компонентами, визначення її структури
та зв'язків між елементами.…………………………………………………5
2 Визначення показників надійності елемента системи.…………………10
3 Визначення надійності системи вцілому.………………………..............13
Висновок……………………………………………………………………..16
Список літератури …………………………………………………………..17
Додаток 1……………….…………………………………………………….19
Додаток 2 …………………………………………………………………….32
Вступ
Загальна теорія систем – науковий напрямок, пов’язаний з розробкою сукупності філософських, методологічних та прикладних проблем аналізу та синтезу складних систем довільної природи.
Система – це множина взаємодіючих елементів (компонентів) та відношень між ними, які вцілому виконують відповідну функцію. Елемент системи – структурна одиниця, яка має риси, що виражають головну якість системи. Для дослідження складних систем у теорії систем використовують системний підхід та системний аналіз.
Системний підхід – це найбільш загальне поняття про системні дослідження, яке засноване на комплексному дослідженні як внутрішньої структури і внутрішніх процесів об’єкта, так і його зовнішніх зв’язків, динаміки розвитку та функціонування.
Системний аналіз, або аналіз складних систем спрямований на розробку на основі системної методології упорядкованої методології досліджень найбільш складних і великих систем та об’єктів великого масштабу.
Більшість залізничних об’єктів, що задіяні у процесі перевезень, можуть класифікуватися як системи різного рівня складності. В контрольній роботі необхідно вирішити задачі щодо створення структури системи, визначення зв’язків між її елементами, а також оцінити надійність кожного елемента зокрема та системи вцілому.
Побудова системи за заданими компонентами, визначення її структури та зв'язків між елементами.
Існує безліч визначень системи. Найбільш розповсюджені: система – це сукупність взаємозалежних елементів, виділена з навколишнього середовища і взаємодіюча з нею як єдине ціле.
Якщо кожна частина системи зв’язана з іншою частиною таким чином, що зміна в одній частині викликає змінe у всіх інших частинах і у всій системі, то система поводиться когерентно, або як ціле. Якщо частини зовсім не зв'язані між собою, то зміна в кожній частині залежить винятково від цієї частини. Таке поводження системи називається незалежним, або фізично адитивним. Цілісність (когерентність) і незалежність (адитивність) це не дві окремих властивості, а крайні ступені однієї властивості. Цілісність системи оцінюється мірою системності:
 (1)
(1)
де
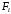 - безліч необхідних станів;
- безліч необхідних станів;
 -
безліч можливих функціональних станів;
-
безліч можливих функціональних станів;
 -
операція перетинання множин;
-
операція перетинання множин;
 -
операція об'єднання множин.
-
операція об'єднання множин.
Через входи з зовнішнього середовища у визначені моменти часу в систему надходить речовина, енергія, інформація; в інші моменти часу результати процесів їхнього перетворення надходять у зовнішнє середовище через виходи. Найбільш типовими є наступні 4 схеми взаємодій:
одномірно-одномірна (один вхідний сигнал і одна вихідна характеристика
 );
);одномірно-многомірна (один вхідний сигнал і кілька вихідних характеристик
 )
)многомірно-одномірна
 ;
;многомірно-многомірні
 ;
;
Елементи і компоненти, входи і виходи по різному зв'язані між собою. Існують такі види зв'язків: незамкнуті, замкнуті, складні.
Основні
незамкнуті
зв'язки: а) прямий послідовний (простий)
зв'язок
 ;
;

б) зв'язок, що паралельно розподіляє;
с) зв'язок, що паралельно з'єднує

d) послідовний непрямий зв'язок між системами;

е) паралельний зв'язок з розширенням:

Замкнуті зв'язки формуються за допомогою зворотнього зв'язку: тобто зв'язок між входом і виходом того ж самого елемента системи. Зворотній зв'язок, що зменшує вплив вхідного сигналу на вихідний, називається негативним, а той, що збільшує цей вплив, називається позитивним. Негативний зворотній зв'язок сприяє відновленню рівноваги в системі, що порушена зовнішнім впливом. Позитивний зворотній зв'язок підсилює відхилення від стану рівноваги в системі.
Замкнуті зв'язки бувають наступних типів:
1. Власний зворотній зв'язок

2. Прямий зворотній зв'язок

3. Непрямий зворотній зв'язок двох видів:
а)

б)

Складні зв'язки
У складних системах виникає безліч комбінацій зв'язків між окремими елементами і підсистемами. Найбільш поширені:
1. Зворотній паралельний розподільний зв'язок

2. Зворотній паралельний сполучний зв'язок

3. Паралельно-послідовний зв'язок

Аналіз елементів, компонентів і зв'язків між ними дозволяє встановити, з чого складається система. А при дослідженні системи важливо довідатися, як вона улаштована й організована. Це характеризує структуру і функції системи. Можна виділити наступні основні структури.
Лінійна структура:

Деревоподібна структура:

Мережева структура:

Матрична структура:

У роботі 1 необхідно побудувати структурну схему залізничної станції або її інформаційної системи відповідно до завдання (додаток 1, завдання 1).
Приклад рішення задачі:
Побудувати структурну схему проміжної станції з наступними характеристиками: 3 (три) приймально-відправні колії, поперечний тип, двоколійна лінія, примикання вантажного двору з непарної сторони.
Рішення: у першу чергу необхідно виділити основні елементи, що задіяні в технологічному процесі роботи станції й описати їх відповідними блоками.
Оскільки вхідним потоком у даній системі є состави, що надходять на станцію, виділяємо наступні елементи:
елементи, через які состави надходять на станцію:
- вхідна стрілка непарної горловини
Вх Н
- вхідна стрілка парної горловини
Вх П
елементи, що приймають состави, тобто приймально-відправні колії (ПВК). Їх кількість складає 3 (три).
ПВК…
У блоці проставляється № шляху в залежності
від його розташування
елементи, що обробляють вагони на станції
ВР
- вантажний двір
4) елементи, через які склади виходять
зі станції:
Вих Н
- вихідна стрілка непарної горловини
- вихідна стрілка парної горловини
Вих П
Усі приведені вище елементи поєднуються в єдину систему, що має мережну структуру.


Вх Н
Вх П






I ГК
ПВК 3
ПВК 5
ПВК 4
II ГК









ВР
Вих Н
Вих П



Рис. 1 – Структурна схема проміжної станції
Таким чином, одержуємо систему з 10 елементів, об'єднаних у єдиною структурою зі складними зворотними паралельно-послідовними зв'язками.
Визначення показників надійності елемента системи.
Кожна окремо взята система характеризується надійністю. Надійність системи – це її здатність до безвідмовної роботи протягом заданого проміжку часу у визначених умовах. У теорії надійності розрізняють два типи відмов – раптові і поступові. Раптове відмовлення – це миттєвий вихід з ладу у випадковий момент часу. Поступове відмовлення зв'язане з поступовим погіршенням характеристик системи, і як тільки параметри системи виходять за визначені межі, система вважається, що відмовила.
Надійність
системи
залежить
від
складу
та
кількості
елементів,
що утворюють її,
від
засобу
їх
об’єднання
в систему
(структури)
та
від
характеристик кожного
окремого
елементу.
Для оцінки
надійність
системи
та
її
елементів
існують
кількісні
характеристики. Надійність
елементу
– це
імовірність
того, що
даний
елемент
в даних
умовах
буде працювати
безвідмовно
протягом
часу
t, позначається
 .
Функція
.
Функція
 називається
законом надійності.
Звісно,
що
при
називається
законом надійності.
Звісно,
що
при
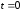
 ,
а при
,
а при

 ,
тобто
спадає.
,
тобто
спадає.
Ненадійністю
елемента
називається
імовірність
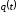 того, що
елемент
відмовить
протягом
часу
того, що
елемент
відмовить
протягом
часу
 ,тобто
,тобто
 .
Графіки функцій
.
Графіки функцій
 та
та
 представлені
на рис. 2.
представлені
на рис. 2.

Рис. 2 – Графіки функцій надійності та ненадійності елемента
У даній роботі розглядається раптове відмовлення системи. Для раптових відмовлень використовується експоненційний закон
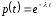 ,
(2)
,
(2)
де
 –
імовірність безвідмовної роботи
елемента;
–
імовірність безвідмовної роботи
елемента;
 –середнє
число відмов в одиницю часу, що приходиться
на один працюючий елемент (інтенсивність
відмови):
–середнє
число відмов в одиницю часу, що приходиться
на один працюючий елемент (інтенсивність
відмови):
 ,
(3)
,
(3)
де
 – середній інтервал часу між двома
послідовними відмовами елемента
– середній інтервал часу між двома
послідовними відмовами елемента
 .
(4)
.
(4)
Вихідні дані для визначення показників надійності кожного елемента (інтенсивність відмови та імовірність безвідмовної роботи елемента) знаходяться в завданні (додаток 1, завдання 2).
Розглянемо як приклад визначення надійності для кожного елемента в задачі 1.
Рішення: система складається з 10 елементів, для кожного з яких задані статистичні дані щодо інтервалів між відмовами кожного з елементів за розрахунковий період у годинах. Як відомо, для статистичної оцінки параметрів необхідна наявність репрезентативної виборки. В даному завданні наведено частину цієї виборки. Приведемо ці дані у вигляді таблиці 1.
Таблиця 1 – Інтервали між двома послідовними відмовами елементів системи
|
№ спосте-реження |
№ елементу | |||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 | |
|
1 |
0,6 |
0,5 |
0,4 |
0,8 |
1,0 |
1,2 |
0,9 |
1,1 |
0,8 |
0,5 |
|
2 |
0,4 |
0,9 |
1,5 |
1,6 |
1,3 |
1,4 |
1,2 |
1,3 |
1,1 |
1,4 |
|
3 |
0,5 |
0,4 |
0,6 |
0,8 |
1,0 |
1,2 |
1,5 |
1,2 |
1,1 |
1,0 |
|
4 |
0,6 |
0,7 |
0,9 |
1,1 |
1,3 |
1,5 |
1,4 |
1,0 |
1,1 |
1,2 |
|
5 |
0,8 |
1,1 |
1,2 |
0,7 |
0,5 |
1,5 |
1,6 |
1,7 |
1,2 |
1,4 |
|
6 |
0,7 |
0,8 |
0,6 |
1,2 |
1,3 |
0,5 |
0,8 |
0,9 |
1,4 |
1,5 |
|
7 |
1,2 |
1,2 |
1,5 |
1,4 |
0,8 |
0,9 |
0,9 |
1,5 |
1,4 |
1,4 |
|
8 |
0,8 |
0,9 |
0,5 |
0,6 |
1,7 |
1,4 |
1,2 |
1,1 |
1,2 |
1,1 |
|
9 |
1,4 |
1,3 |
1,5 |
1,5 |
0,9 |
0,8 |
0,9 |
1,5 |
1,3 |
1,4 |
|
10 |
1,5 |
1,2 |
1,4 |
1,3 |
1,2 |
1,1 |
1,2 |
0,9 |
0,8 |
1,2 |
|
11 |
1,4 |
1,3 |
1,2 |
1,2 |
0,8 |
0,9 |
1,2 |
1,3 |
1,4 |
1,5 |
|
12 |
1,8 |
1,9 |
1,2 |
1,4 |
1,6 |
1,1 |
0,7 |
0,8 |
1,4 |
1,3 |
|
13 |
1,2 |
1,2 |
1,5 |
1,6 |
0,9 |
0,8 |
0,7 |
1,2 |
1,3 |
1,2 |
|
14 |
1,4 |
1,3 |
1,2 |
0,9 |
0,9 |
1,2 |
1,2 |
1,3 |
1,4 |
1,5 |
|
15 |
1,1 |
1,1 |
0,9 |
0,8 |
1,2 |
1,1 |
1,3 |
1,4 |
1,5 |
1,6 |
|
16 |
1,5 |
1,2 |
1,1 |
1,1 |
0,9 |
0,9 |
0,8 |
0,9 |
1,3 |
1,3 |
|
17 |
1,1 |
1,1 |
1,6 |
1,7 |
1,8 |
1,9 |
2,0 |
1,7 |
1,4 |
0,9 |
|
18 |
1,0 |
1,2 |
0,9 |
1,4 |
1,5 |
1,3 |
1,1 |
0,8 |
0,7 |
0,8 |
|
19 |
1,1 |
1,2 |
1,3 |
1,4 |
1,5 |
1,6 |
1,2 |
1,3 |
1,1 |
0,9 |
|
20 |
1,0 |
1,2 |
1,5 |
1,1 |
1,4 |
1,3 |
0,8 |
0,8 |
0,9 |
1,1 |
На
підставі формул (2–4) визначаються
показники надійності (інтенсивність
відмови
 та
імовірність безвідмовної роботи
та
імовірність безвідмовної роботи
 )
для кожного елементу, які зводяться у
таблицю 2.
)
для кожного елементу, які зводяться у
таблицю 2.
Таблиця 2 – Результати розрахунків показників надійності елементів системи
|
№ елем |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
1,05 |
1,09 |
1,13 |
1,18 |
1,18 |
1,18 |
1,13 |
1,19 |
1,19 |
1,21 |
|
|
0,95 |
0,92 |
0,88 |
0,85 |
0,85 |
0,85 |
0,88 |
0,84 |
0,84 |
0,83 |
|
|
|
|
|
|
|
|
|
|
|
|
Визначення надійності системи вцілому.
Нехай система S складається з n елементів, показники надійності яких відомі. Визначимо надійність системи. Вона залежить від того, як елементи об'єднані в систему, тобто від її структури.
I. Розглянемо систему без резервування, тобто відмовлення будь-якого елемента призводить до відмовлення системи в цілому. У сенсі надійності така структура рівносильна послідовному з'єднанню елементів.
Нехай P – надійність системи S, а Pi – надійності елементів Эi (рис. 3)

Рис. 3 – Послідовне з’єднання елементів
Нехай елементи відмовляють незалежно один від одного, тоді за правилом множення імовірностей незалежних подій маємо:
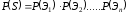 ,
чи
,
чи
 .
(5)
.
(5)
Якщо
 ,
то
,
то .
.
II. Система з резервуванням.
Резервні
елементи включаються в систему паралельно
тим, надійність яких недостатня. Нехай
елементи Э1
і Э2
незалежні по відмовах, а відповідні
надійності (імовірності безвідмовної
роботи) дорівнюють Р1
і Р2,
знайдемо
 (рис.
4).
(рис.
4).

Рис. 4 – Паралельне з’єднання елементів
Розглянемо
імовірність відмови системи
 .
Щоб подія
.
Щоб подія (відмова всієї системи) відбулася
необхідно, щоб відмовили обидва елементи,
тобто за правилом множення імовірностей
незалежних подій маємо:
(відмова всієї системи) відбулася
необхідно, щоб відмовили обидва елементи,
тобто за правилом множення імовірностей
незалежних подій маємо:
 ,
(6)
,
(6)
використовуючи поняття ненадійності системи і ненадійності елементів маємо:
 ,
(7)
,
(7)
де
 – відповідні ненадійності елементів
(імовірність того, що елемент відмовить),
які визначаються як
– відповідні ненадійності елементів
(імовірність того, що елемент відмовить),
які визначаються як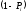
Тоді маємо:
 ;
;
 .
(8)
.
(8)
Якщо
число дублюючих один одного незалежних
елементів дорівнює n, то надійність
системи
 ,
якщо
,
якщо ,
то
,
то .
.
Для оцінки надійності складної структури, що включає в себе послідовні та паралельні об’єднання елементів, доцільно поділити систему на ряд підсистем, що не мають загальних елементів. На рис. 5 наведений приклад розподілення складної системи з 7 (семи) елементів. Тут підсистема І містить два елементи, що пов’язані послідовно, підсистема ІІ – два паралельно зв’язаних елементи, підсистема ІІІ об’єднує послідовно І та ІІ підсистеми, IV підсистема – два паралельно зв’язаних елементи, V підсистема послідовно поєднує IV підсистему з п’ятим елементом.


Рис. 5 – Складна система з паралельними та послідовними зв’язками між елементами
Відповідно до формул (5,8) отримуємо
 (9)
(9)
У даній роботі розглядаються складні системи з елементами резервування.
Вихідні дані наведено в завданні (додаток 1, завдання 3) і являють собою частину елементів зі структур, що будуються в задачі 1.
Розглянемо як приклад наступну схему (рис. 6)



Рис. 6 – Структурна схема приймально-відправного парку дільничної станції
На рисунку представлений приймально-відправний парк дільничної станції з 3 (трьома) приймально-відправними коліями. Відносно до схеми, прийом потяга може здійснюватися на будь-яку колію парку, так само, як і відправлення з кожного з них.
У вигляді таблиці наведено величини імовірностей безвідмовної роботи для кожного з елементів
Таблиця 3 – Імовірності безвідмовної роботи для елементів системи
|
Назва елементу |
Вхідна горловина (1) |
ПВК 1 (2) |
ПВК 3 (3) |
ПВК 1 (4) |
Вихідна горловина (5) |
|
Імовірність безвідмовної роботи, Р |
0,87 |
0,95 |
0,96 |
0,94 |
0,88 |
Розраховуємо надійність системи за формулами (5,8)

Таким чином, надійність системи складає 0,65.
ВИСНОВОК
У висновку наводяться результати виконаної роботи, виробляється їхній аналіз, а також указуються деякі теоретичні моменти, зв'язані з отриманими результатами, наприклад, висновки щодо структури отриманої в задачі 1 системи.
