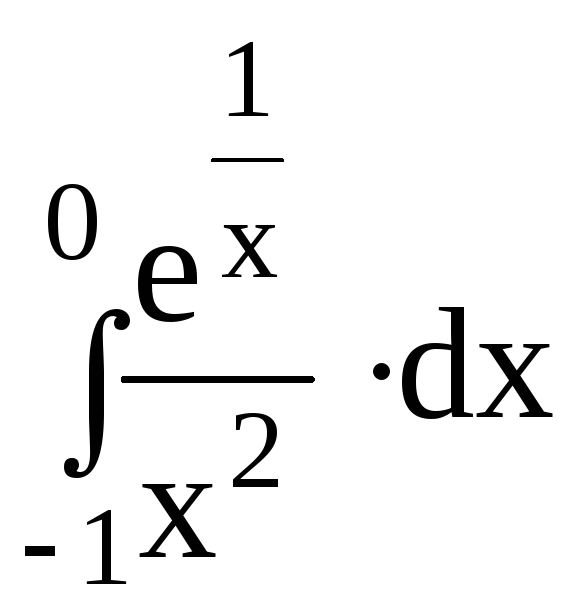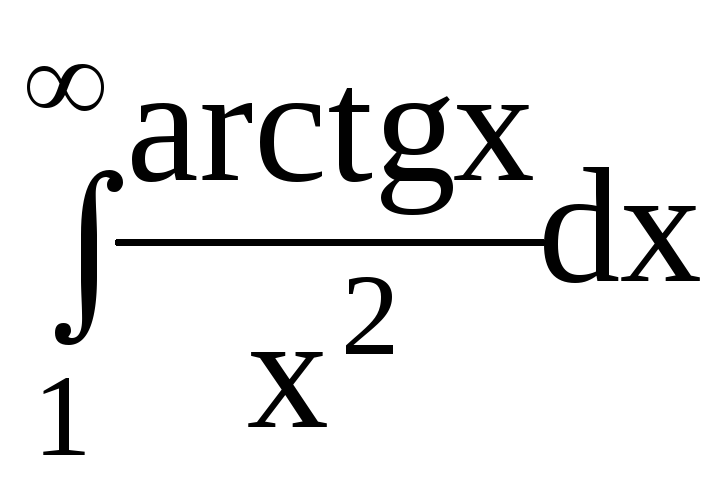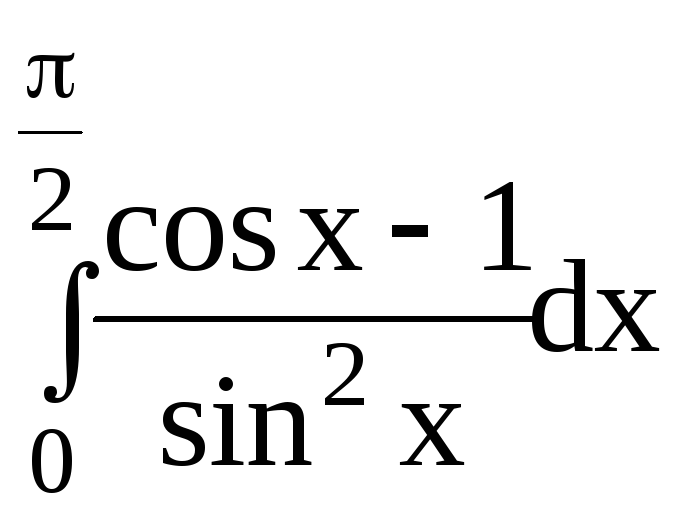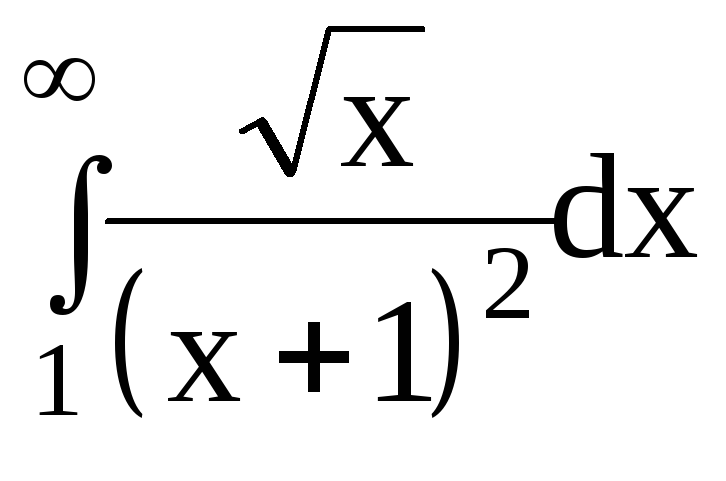Контрольная работа № 3
Интегрирование функций
1.Найти неопределенные интегралы методом подстановки:
|
1.1.
1.2.
1.3.
1.4.
1.5.
1.6.
1.7.
1.8.
1.9.
1.10.
|
1.11.
1.12.
1.13.
1.14.
1.15.
1.16.
1.17.
1.18.
1.19.
1.20.
1.21.
|
1.22.
1.23.
1.24.
1.25.
1.26.
1.27.
1.28.
1.29.
1.30.
|
2.Найти интегралы методом интегрирования по частям:
|
2.1.
|
2.11.
|
2.21.
|
|
2.2.
|
2.12.
|
2.22.
|
|
2.3.
|
2.13.
|
2.23.
|
|
2.4.
|
2.14.
|
2.24.
|
|
2.5.
|
2.15.
|
2.25.
|
|
2.6.
|
2.16.
|
2.26.
|
|
2.7.
|
2.17.
|
2.27.
|
|
2.8.
|
2.18.
|
2.28.
|
|
2.9.
|
2.19.
|
2.29
|
|
2.10.
|
2.20.
|
2.30.
|
3. Найти интегралы от рациональных функций:
|
3.1.
|
3.11.
|
3.21.
| ||||
|
3.2.
|
3.12.
|
3.22.
|
| |||
|
3.3.
|
3.13.
|
3.23.
|
| |||
|
3.4.
|
3.14. |
3.24.
|
| |||
|
3.5.
|
3.15.
|
3.25.
|
| |||
|
3.6.
|
3.16.
|
3.26.
|
| |||
|
3.7.
|
3.17.
|
3.27.
|
| |||
|
3.8.
|
3.18.
|
3.28.
| ||||
|
3.9.
|
3.19.
|
3.29. | ||||
|
3.10.
|
3.20.
|
3.30.
| ||||
4. Найти интегралы:
|
4.1.
|
4.16.
|
|
4.2.
|
4.17.
|
|
4.3.
|
4.18.
|
|
4.4.
|
4.19.
|
|
4.5.
|
4.20.
|
|
4.6.
|
4.21.
|
|
4.7.
|
4.22.
|
|
4.8.
|
4.23.
|
|
4.9.
|
4.24.
|
|
4.10.
|
4.25.
|
|
4.11.
|
4.26.
|
|
4.12.
|
4.27.
|
|
4.13.
|
4.28.
|
|
4.14.
|
4.29.
|
|
4.15.
|
4.30.
|
5.Вычислить определенный интеграл:
|
5.1.
|
5.16.
|
|
5.2.
|
5.17.
|
|
5.3.
|
5.18.
|
|
5.4.
|
5.19.
|
|
5.5.
|
5.20.
|
|
5.6.
|
5.21.
|
|
5.7.
|
5.22.
|
|
5.8.
|
5.23.
|
|
5.9.
|
5.24.
|
|
5.10.
|
5.25.
|
|
5.11.
|
5.26.
|
|
5.12.
|
5.27.
|
|
5.13.
|
5.28.
|
|
5.14.
|
5.29.
|
|
5.15.
|
5.30.
|
6.Вычислить несобственные интегралы или доказать их расходимость:
|
6.1.
|
6.16.
|
|
6.2.
|
6.17.
|
|
6.3.
|
6.18.
|
|
6.4.
|
6.19.
|
|
6.5.
|
6.20.
|
|
6.6.
|
6.21.
|
|
6.7.
|
6.22.
|
|
6.8.
|
6.23.
|
|
6.9.
|
6.24.
|
|
6.10
. |
6.25.
|
|
6.11.
|
6.26.
|
|
6.12.
|
6.27.
|
|
6.13.
|
6.28.
|
|
6.14.
|
6.29.
|
|
6.15.
|
6.30.
|
7. Вычислить указанные величины, используя понятие определенного интеграла:
7.1. Площадь фигуры,
ограниченной параболами у
= х2
и
![]() .
.
7.2. Площадь фигуры, ограниченной кривой у = lnх, прямой х =e2 и осью ох.
7.3. Площадь фигуры, ограниченной кривыми у = ех, у = х ех и осью оу.
7.4. Площадь фигуры, ограниченной кривыми у = sin3x, y = cos3x и осью oy
![]() .
.
7.5. Площадь фигуры, ограниченной окружностью х2 + у2 = 4, прямой у = х-1
и осью оу.
7.6. Длину дуги
кривой у =
е2х+1,
![]() .
.
7.7. Длину дуги кривой у = ln (2х+1).
7.8. Площадь фигуры, ограниченной кривой y = arccos(x) и осями координат.
7.9. Длину дуги
параболы
![]() ,
,![]() .
.
7.10. Длину кривой, заданной параметрически:
![]()
![]()
![]()
7.11. Длину дуги
кривой, заданной параметрически:
![]()
![]()
7.12 Объем тела, ограниченного поверхностью, полученной от вращения дуги
кривой ![]() (
(![]() )
вокруг оси
ох.
)
вокруг оси
ох.
7.13. Объем тела, ограниченного поверхностью, полученной от вращения дуги
кривой
![]()
![]() вокруг
оси ох.
вокруг
оси ох.
7.14. Объем тела, ограниченного поверхностью, полученной от вращения дуги
кривой у
= х ех
![]() вокруг оси
ох.
вокруг оси
ох.
7.15. Объем тела, ограниченного поверхностью, полученной от вращения дуги
кривой у
= lnх
![]() вокруг оси
ох.
вокруг оси
ох.
7.16. Объем тела, ограниченного поверхностью, полученной от вращения дуги
кривой ![]()
![]() вокруг оси
ох.
вокруг оси
ох.
7.17. Площадь поверхности, образованной вращением дуги кривой
у = sinx
![]() вокруг оси ох.
вокруг оси ох.
7.18. Площадь поверхности, образованной вращением дуги кривой
у = х
![]() вокруг оси ох.
вокруг оси ох.
7.19. Площадь поверхности, образованной вращением дуги кривой
![]()
![]() вокруг оси ох.
вокруг оси ох.
7.20. Статический
момент дуги кривой у
= х2 +
1
![]()
относительно оси оу.
7.21. Статический
момент дуги кривой у
= ех
![]() относительно оси ох.
относительно оси ох.
7.22. Координаты
центра тяжести дуги кривой
![]()
![]() .
.
7.23. Координаты
центра тяжести дуги кривой
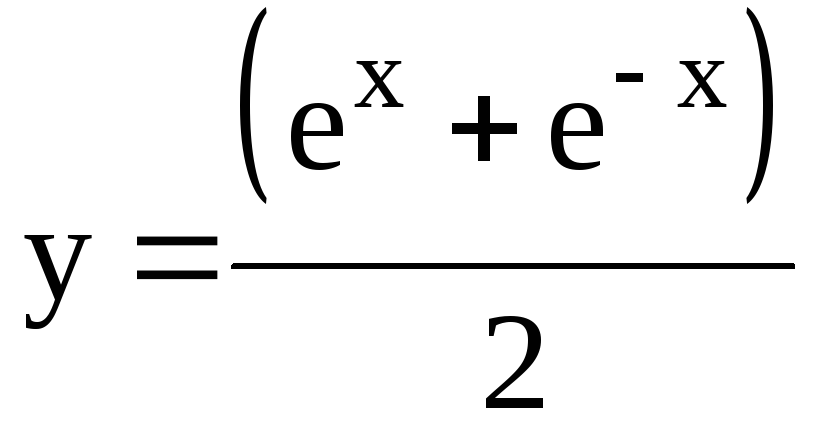
![]() .
.
7.24. Координаты
центра тяжести дуги кривой
![]()
![]() .
.
7.25. Статический момент относительно оси оу фигуры, ограниченной дугой
кривой у = х, прямой х = 1 и осями координат.
7.26. Статический момент относительно оси ох фигуры, ограниченной дугой
кривой
![]() ,
прямойх = е
и осью ох.
,
прямойх = е
и осью ох.
7.27. Координаты
центра тяжести полукруга
![]() .
.
7.28. Координаты центра тяжести фигуры, ограниченной дугой кривой
у = sinх
и осью ох
(
![]() ).
).
7.29. Координаты центра тяжести фигуры, ограниченной дугой кривой
![]() и осью
oх.
и осью
oх.
7.30. Координаты центра тяжести фигуры, ограниченной дугой кривой
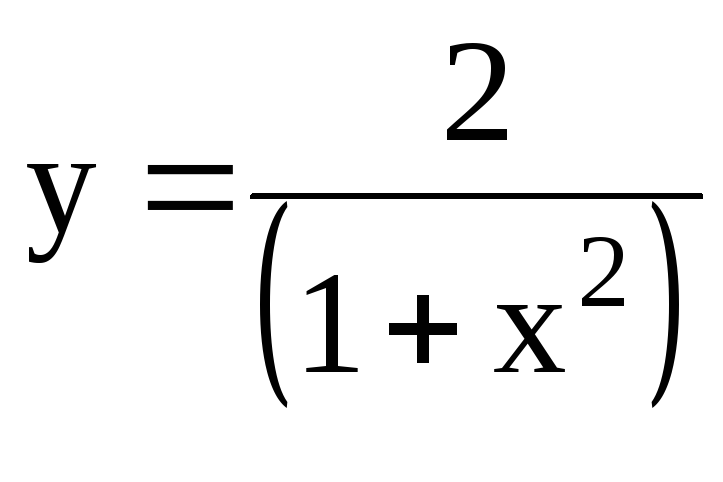 ,
прямой х =
-1, х
= 1 и осью
ох.
,
прямой х =
-1, х
= 1 и осью
ох.

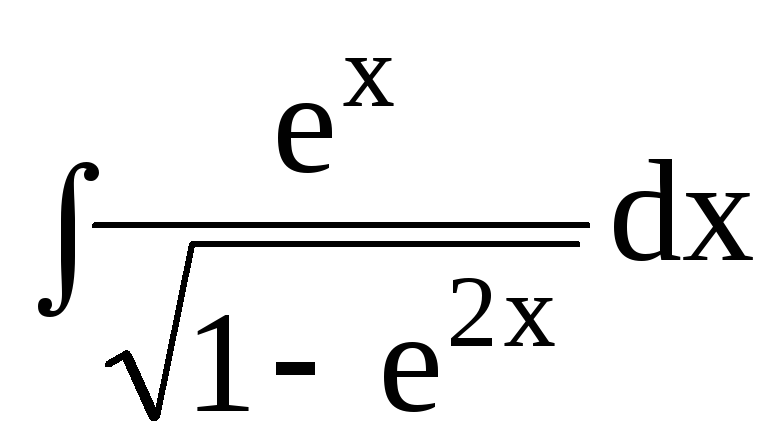


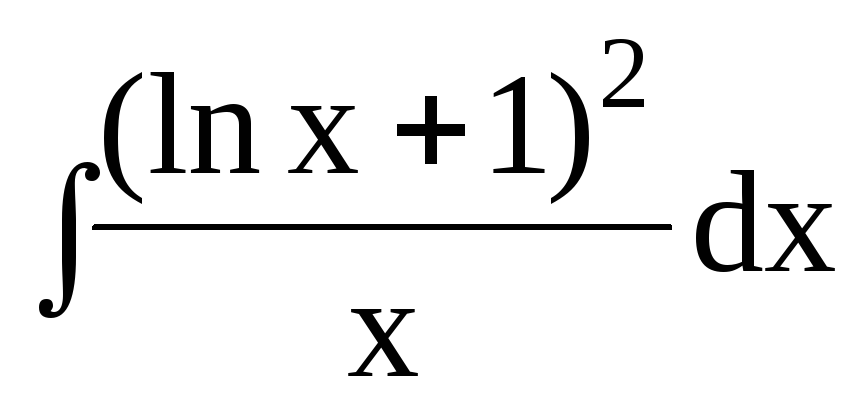
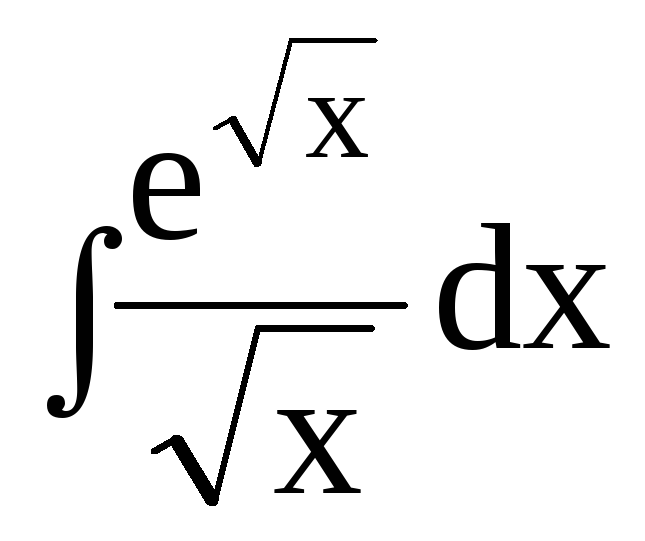
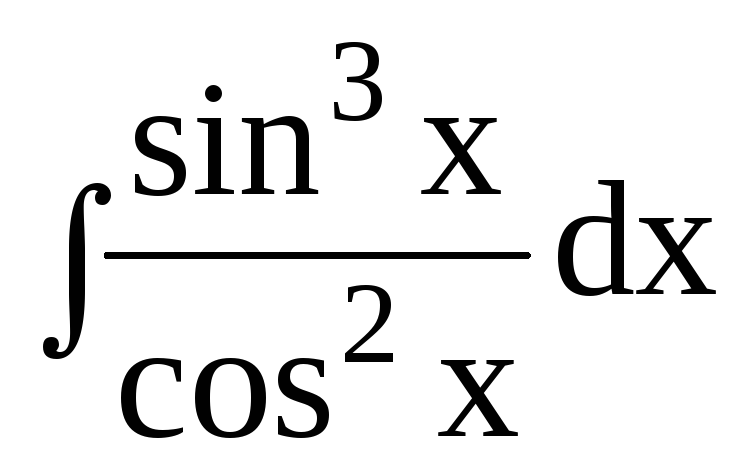

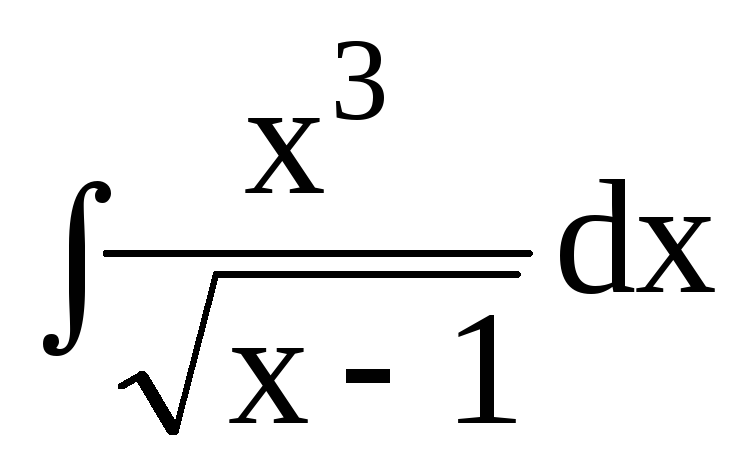

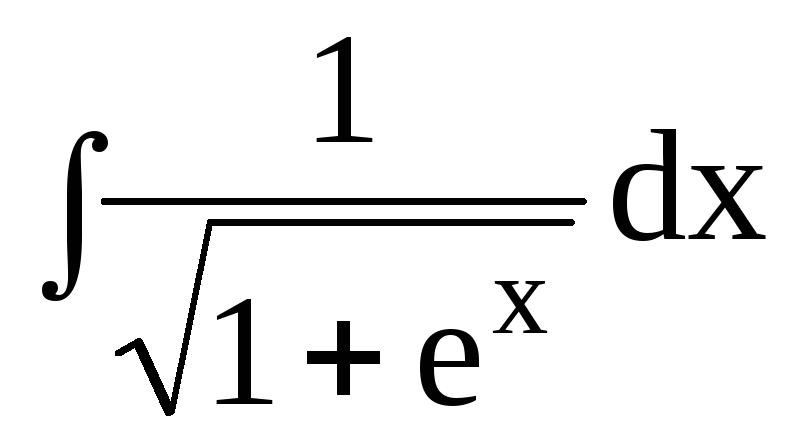
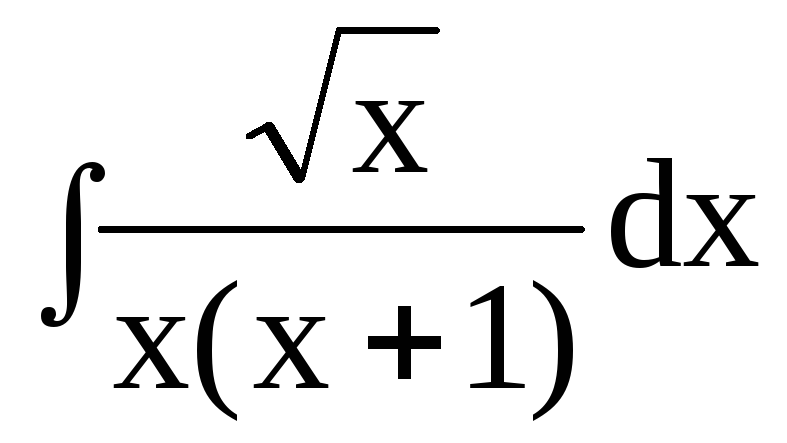
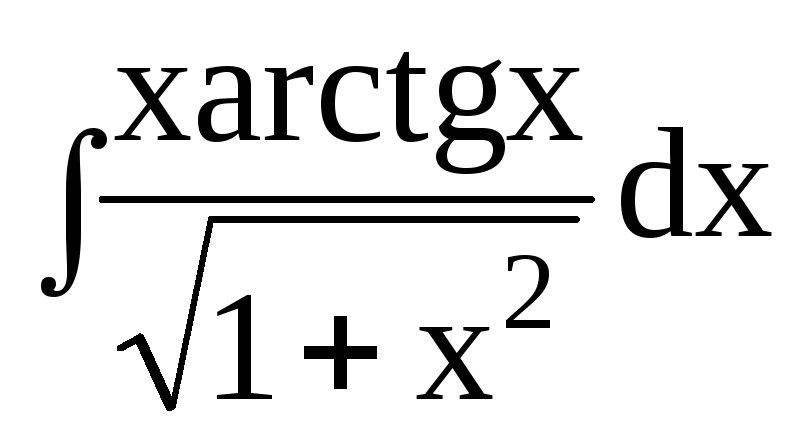
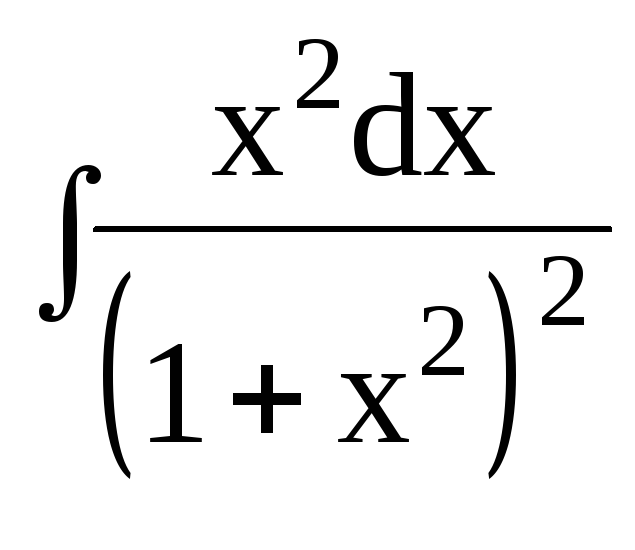
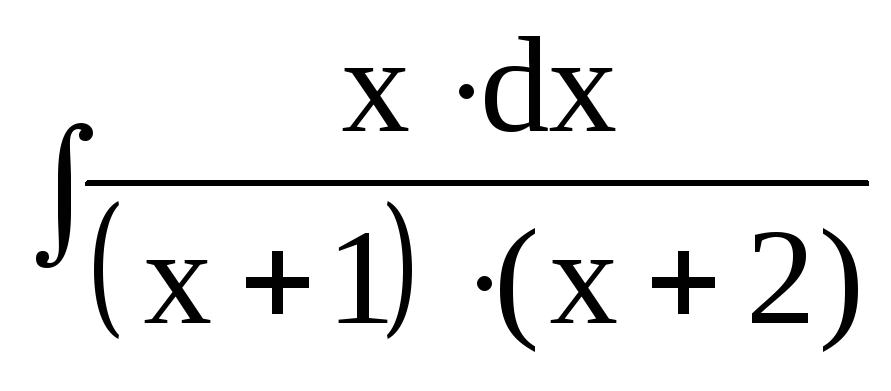
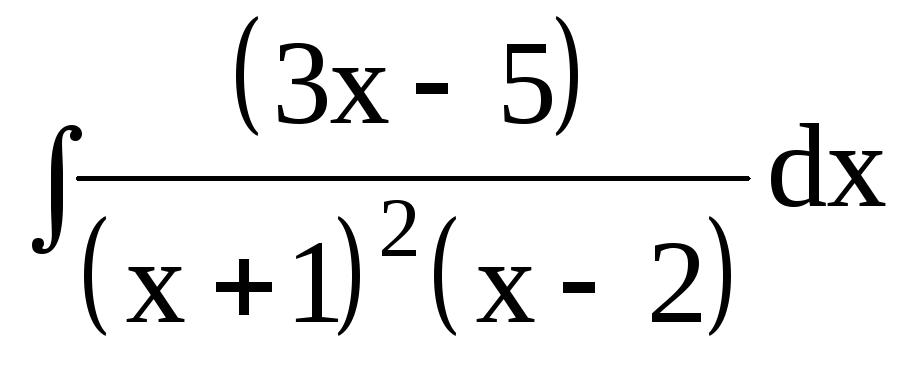

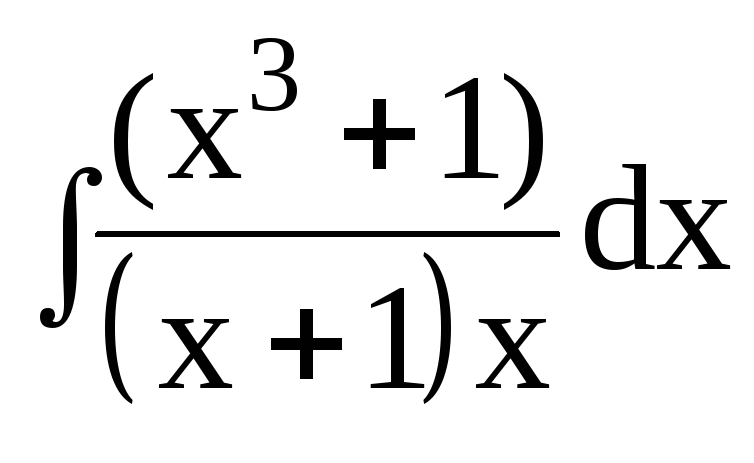
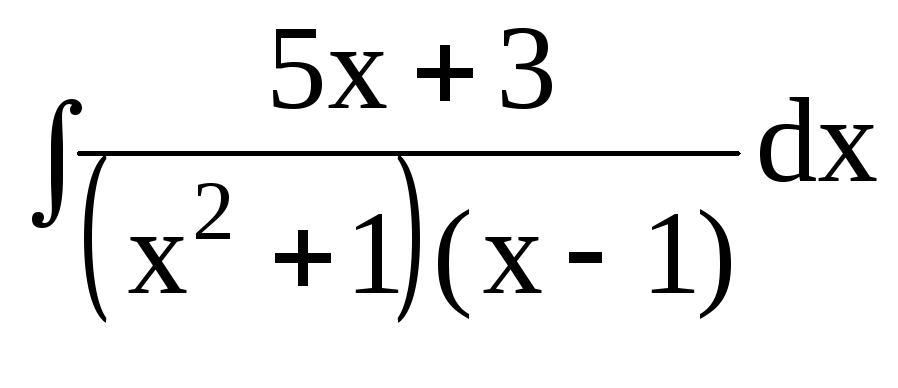
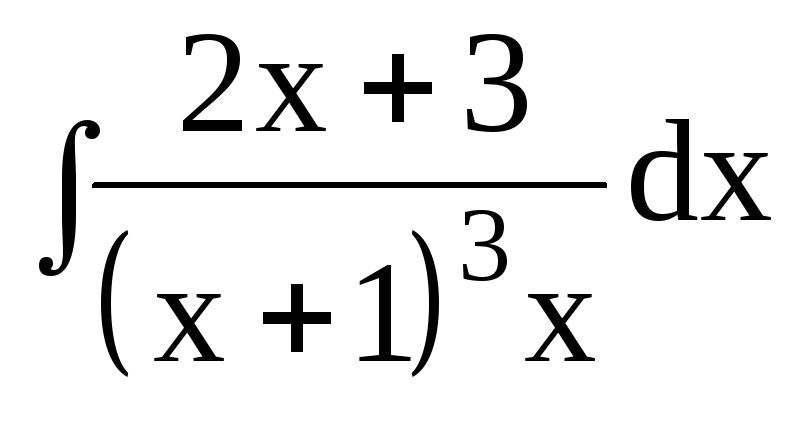
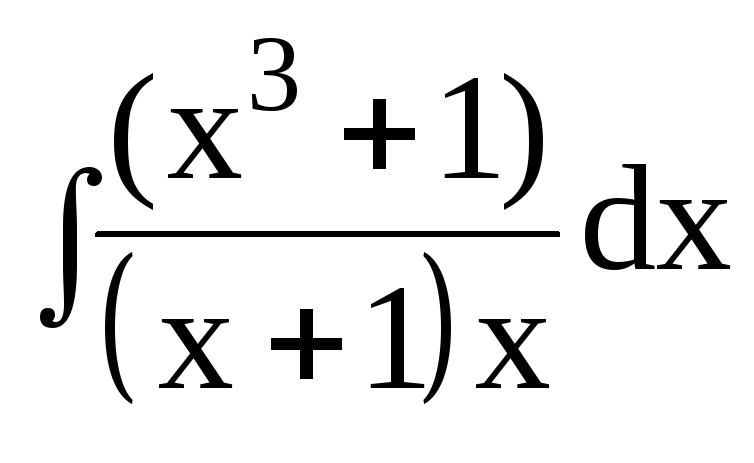
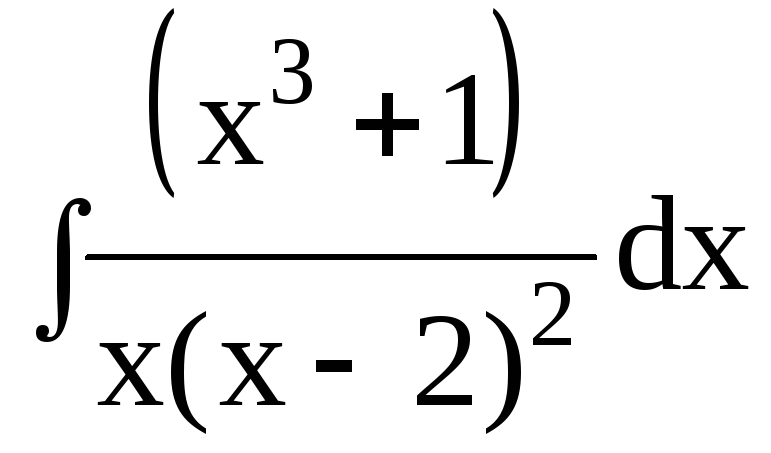

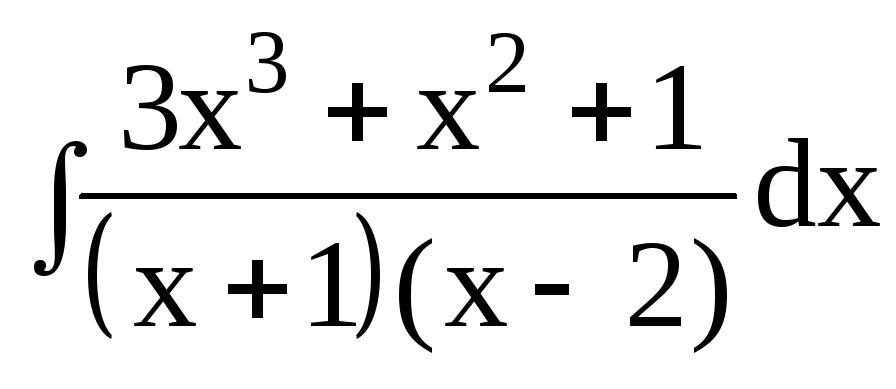
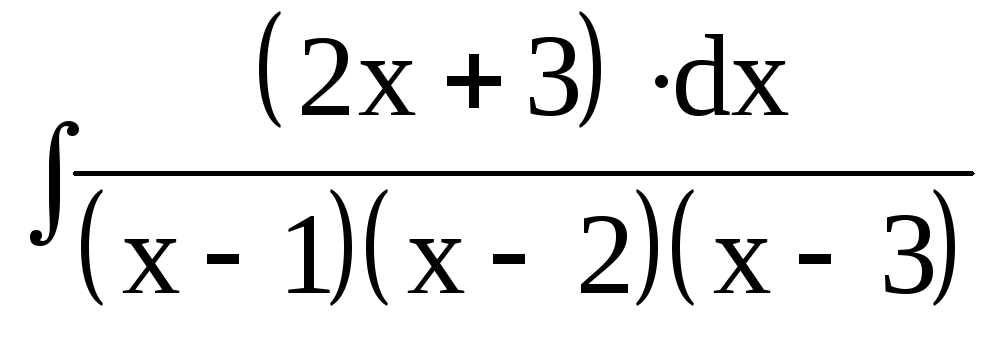
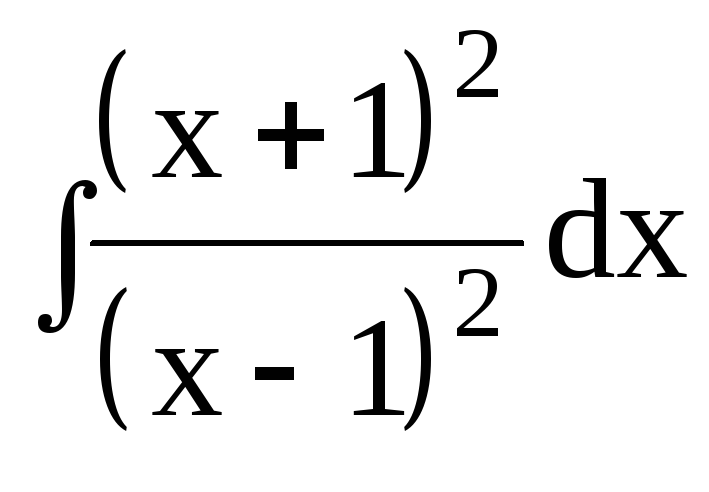
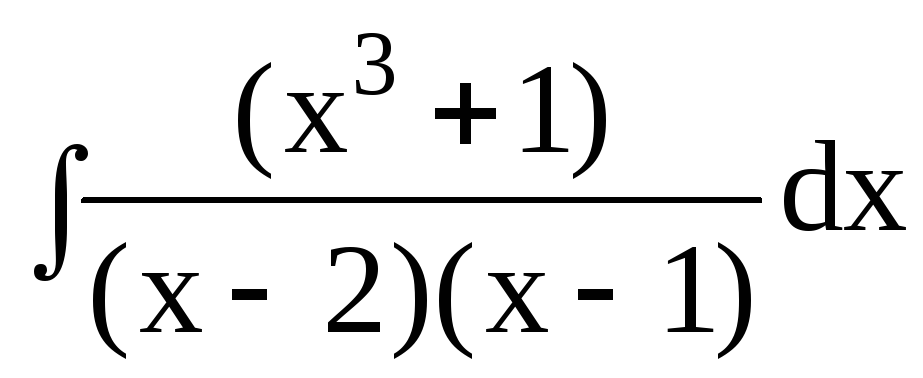
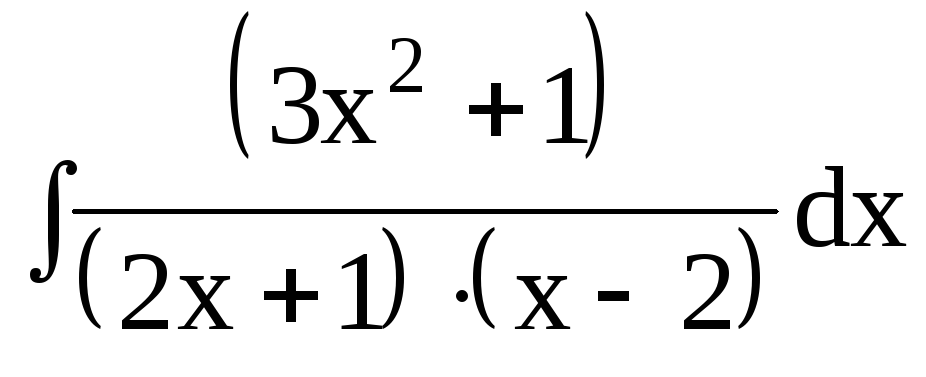
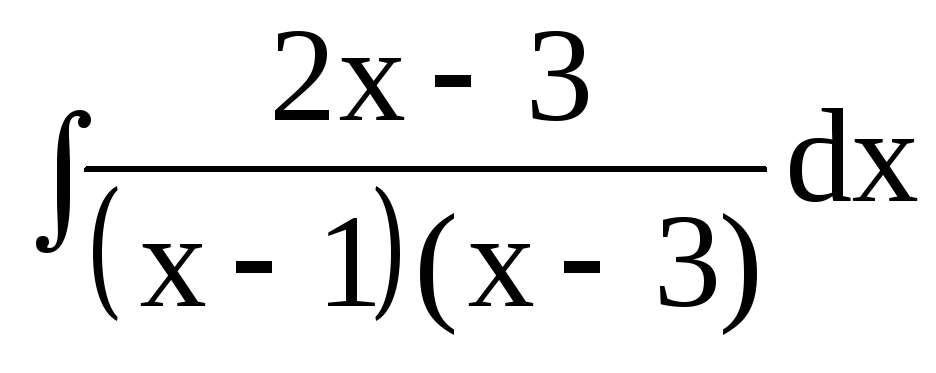
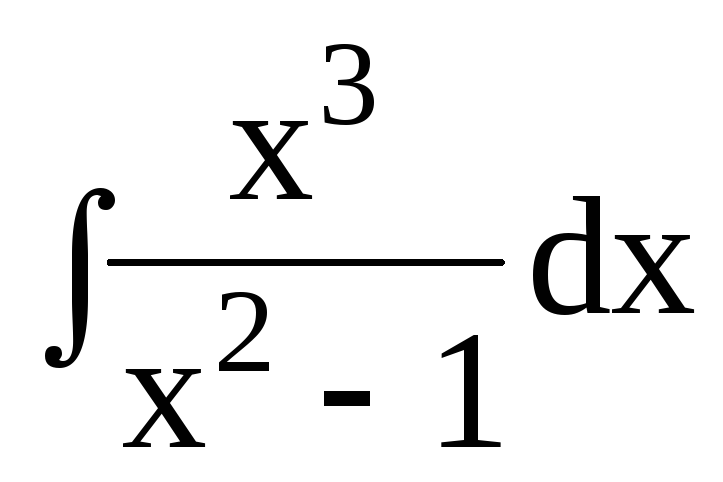
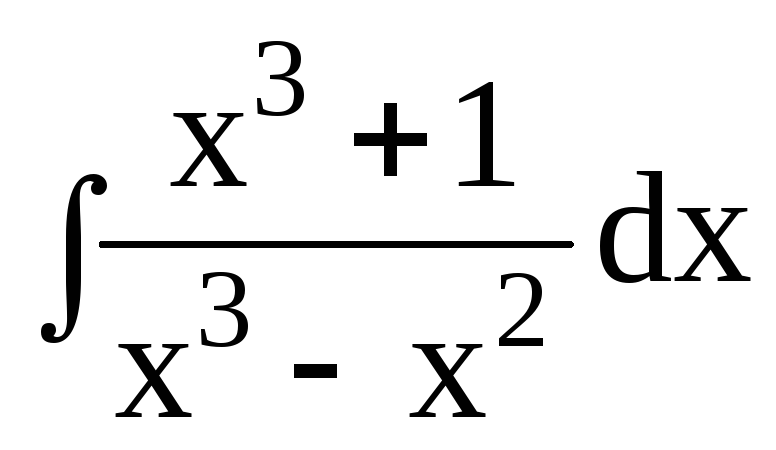
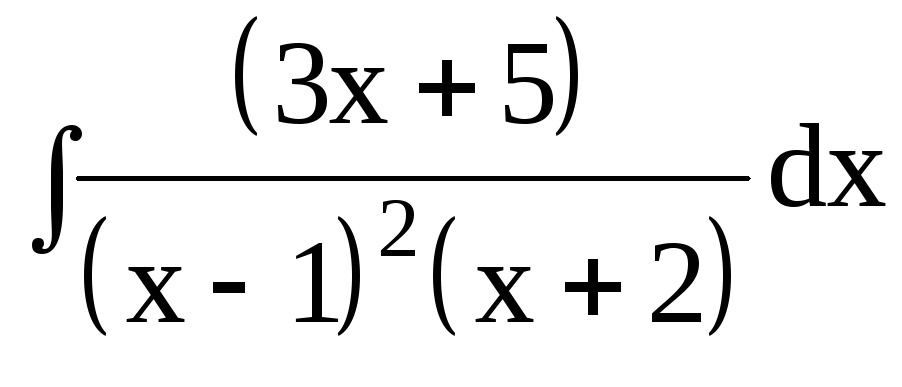
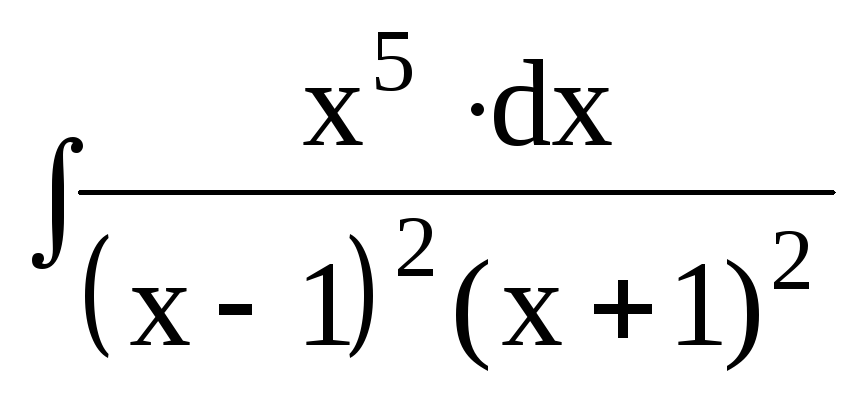
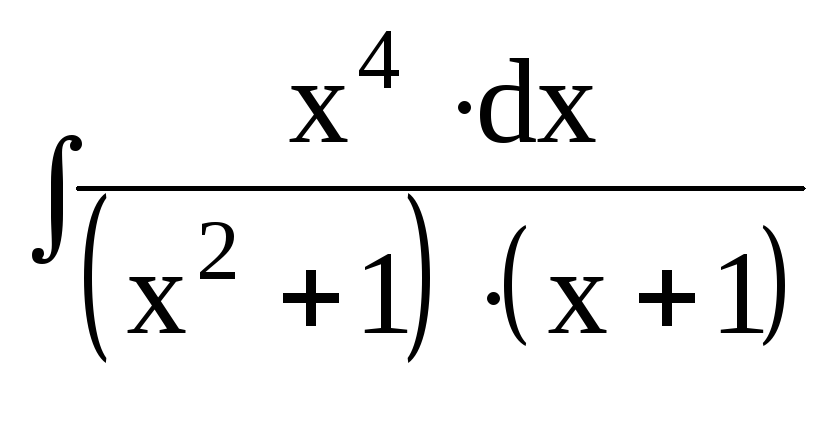
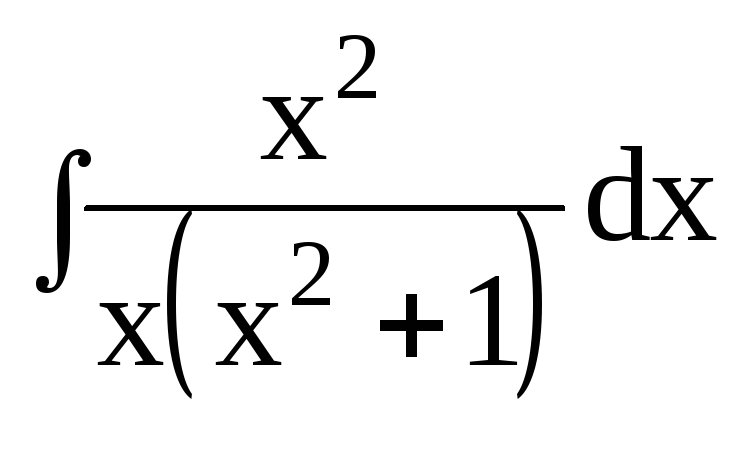
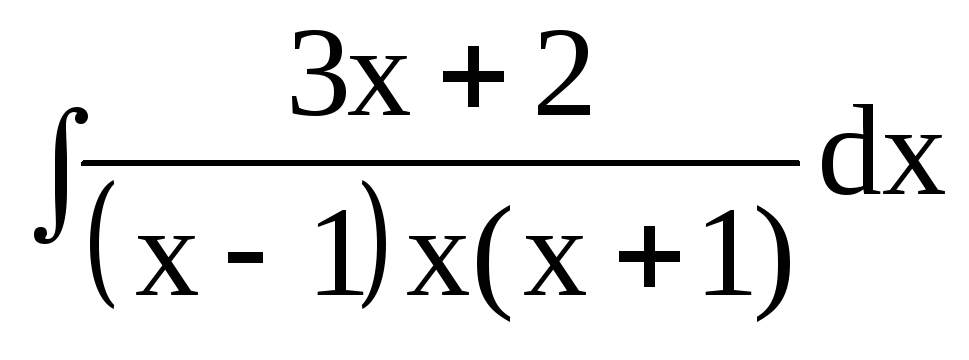
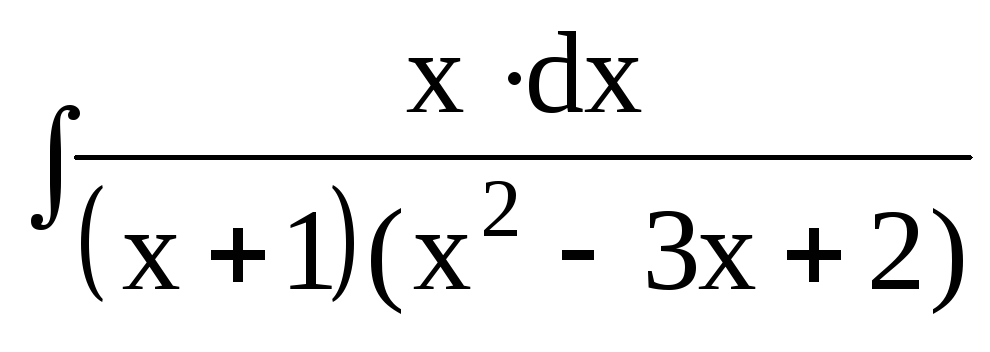
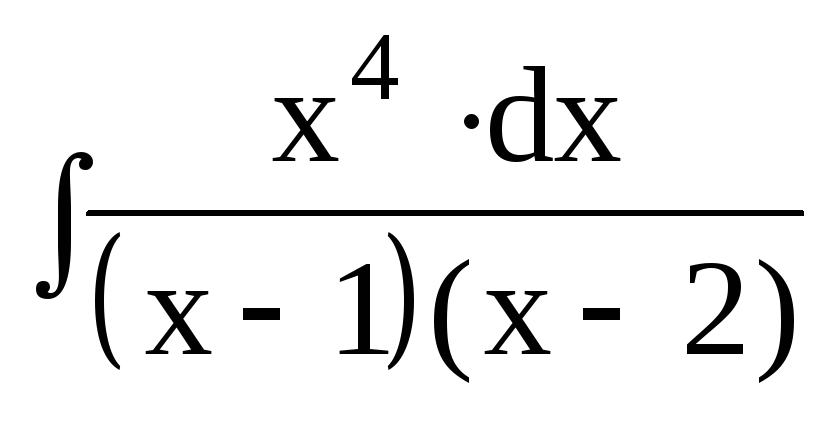
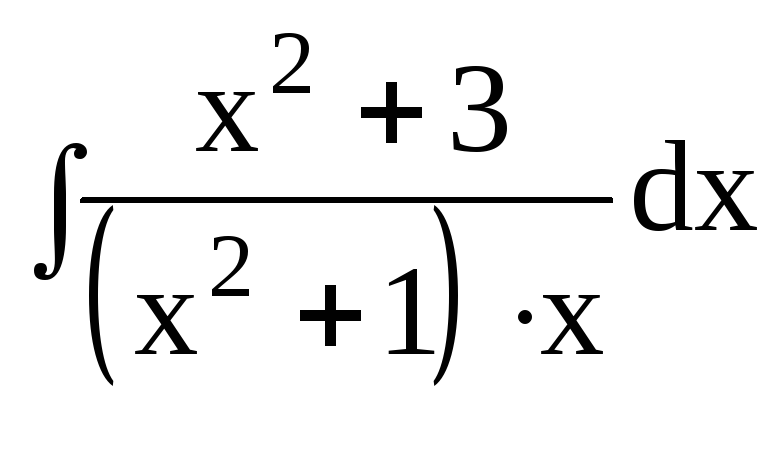

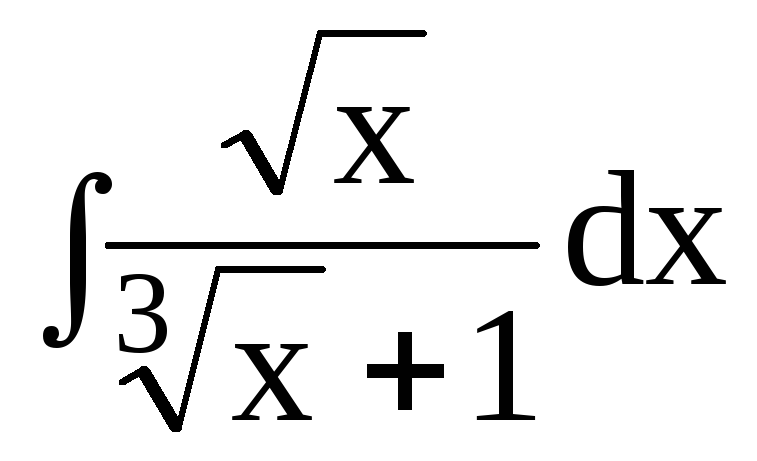

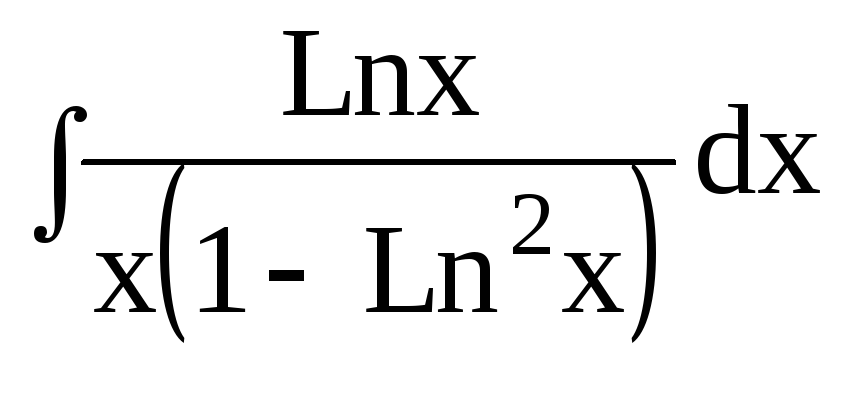
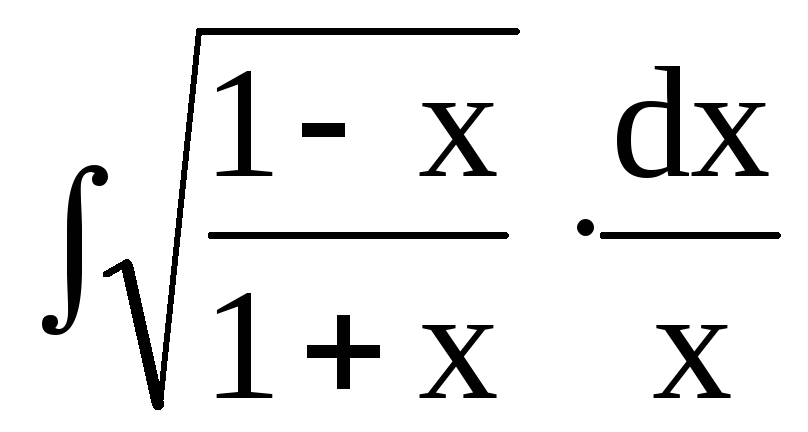
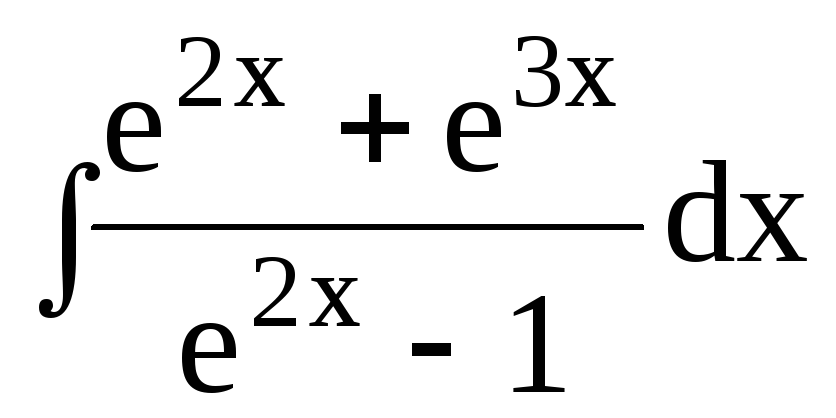
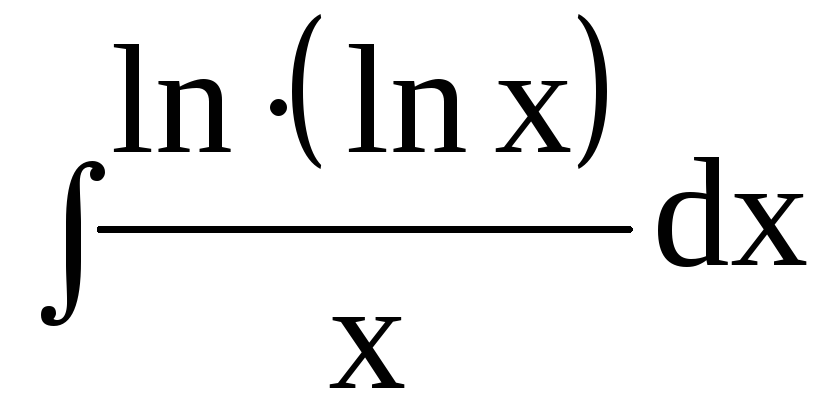


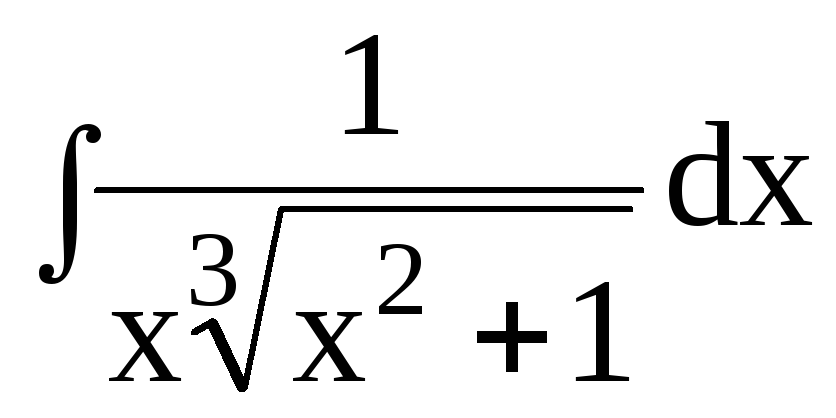
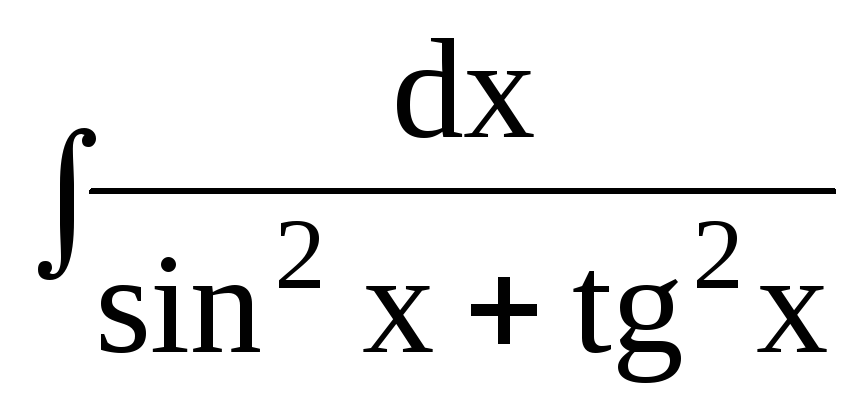
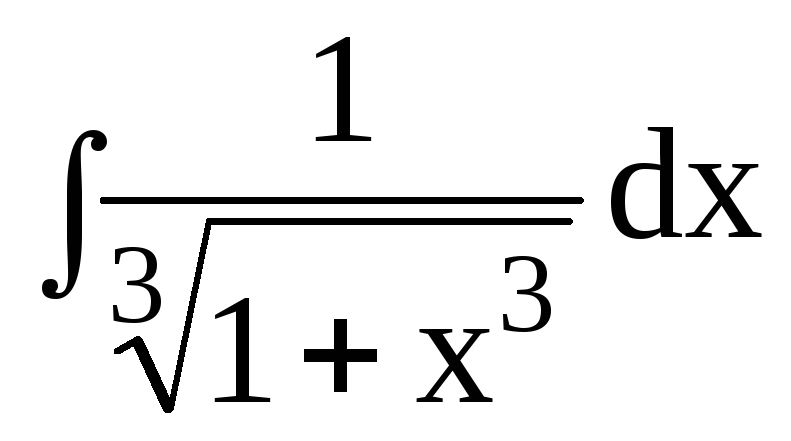
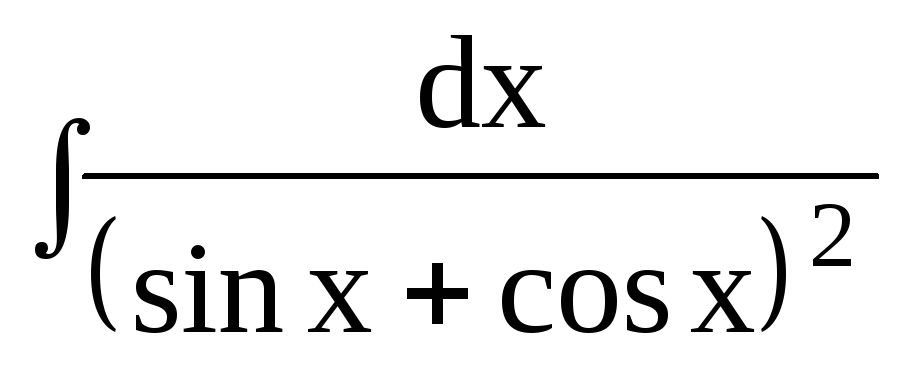
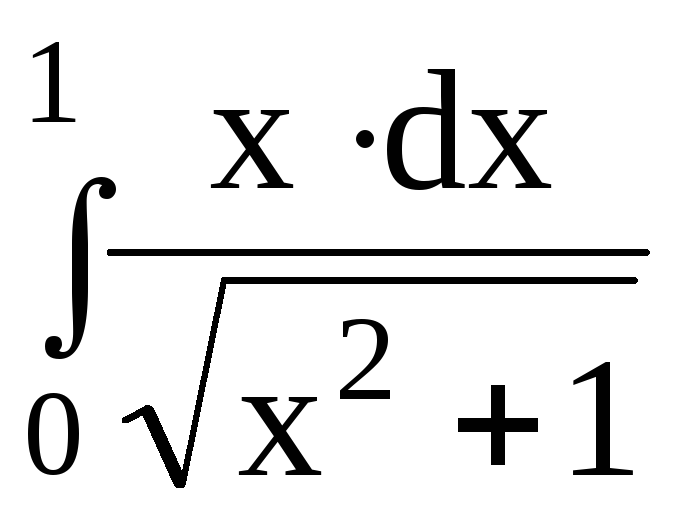
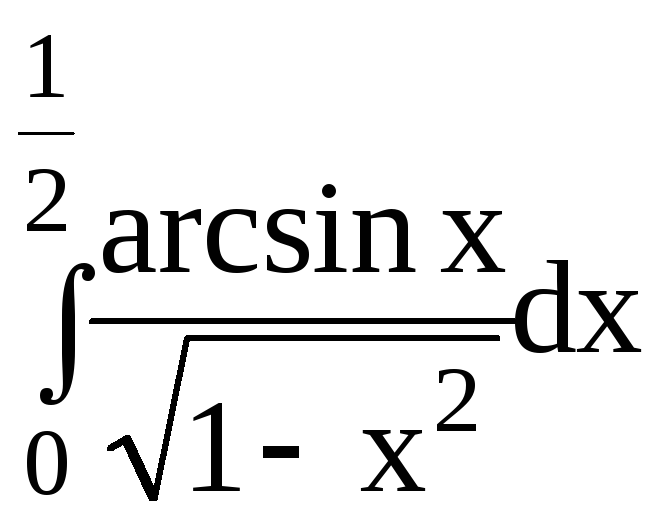

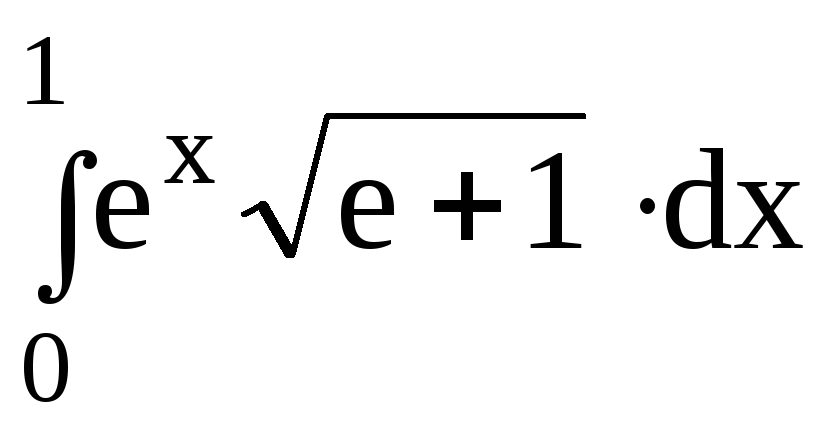

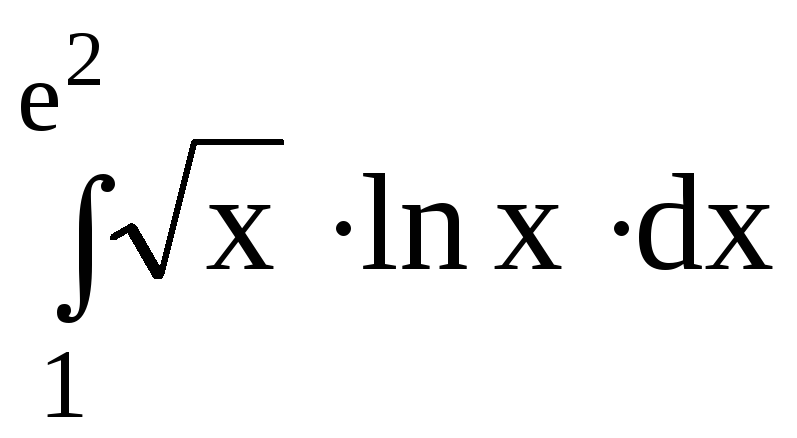

 dx
dx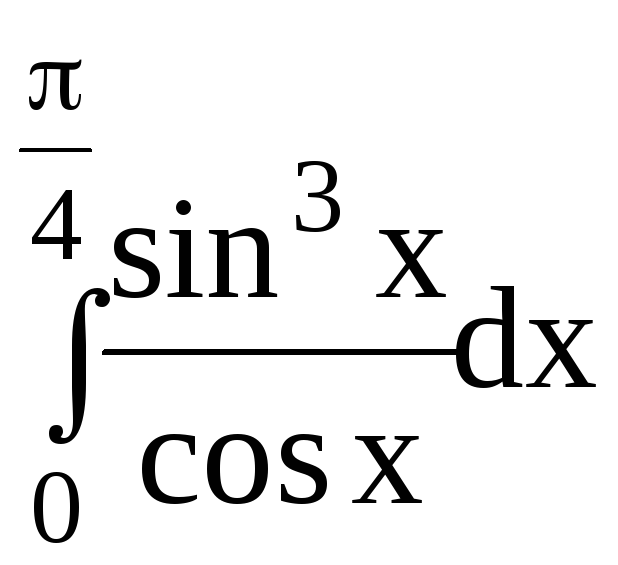
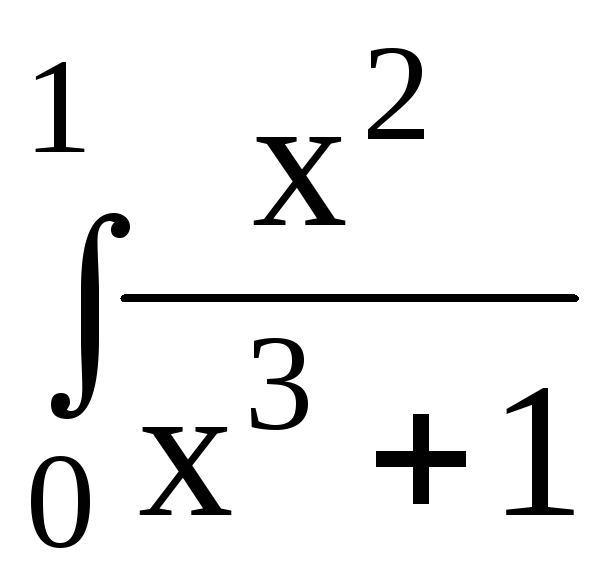 dx
dx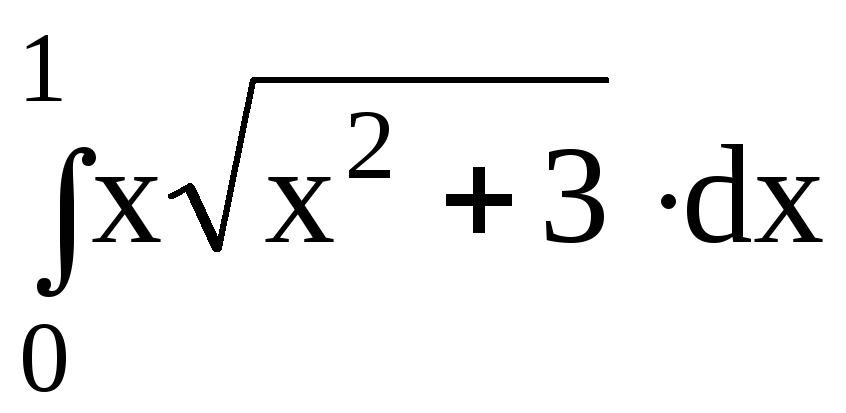
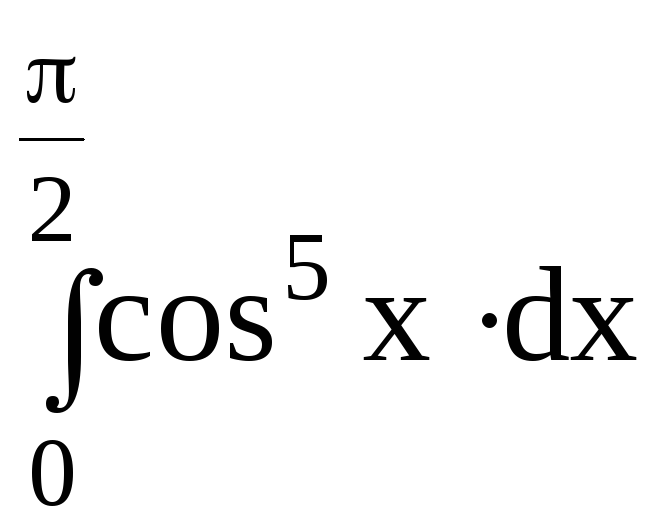

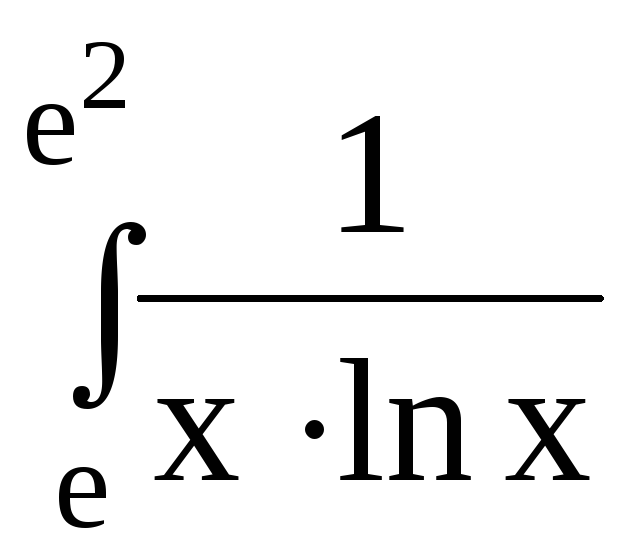 dx
dx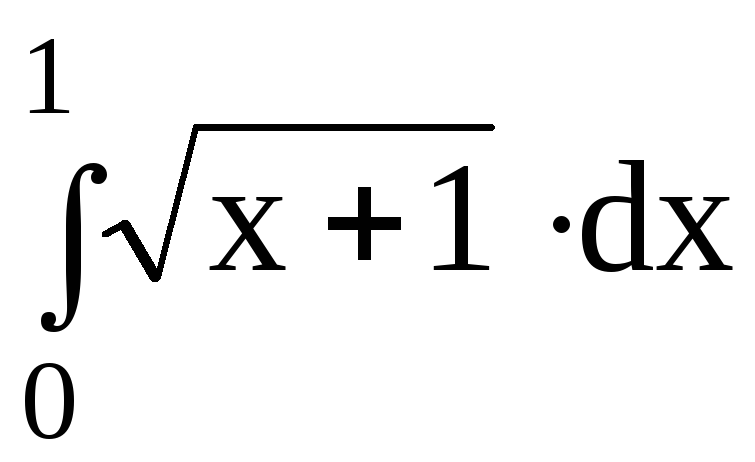
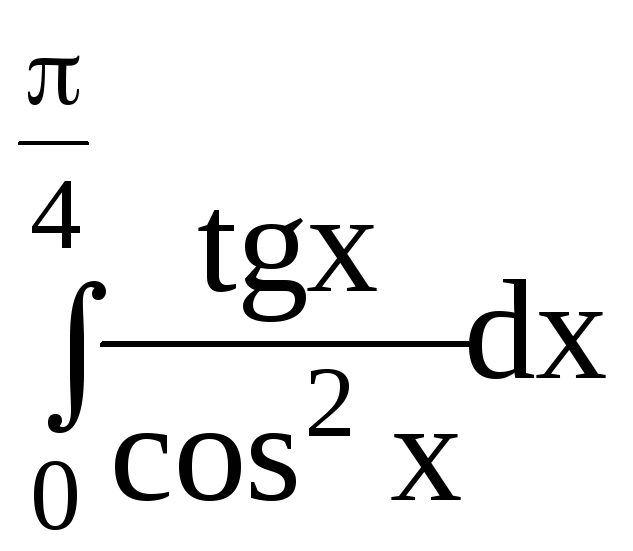
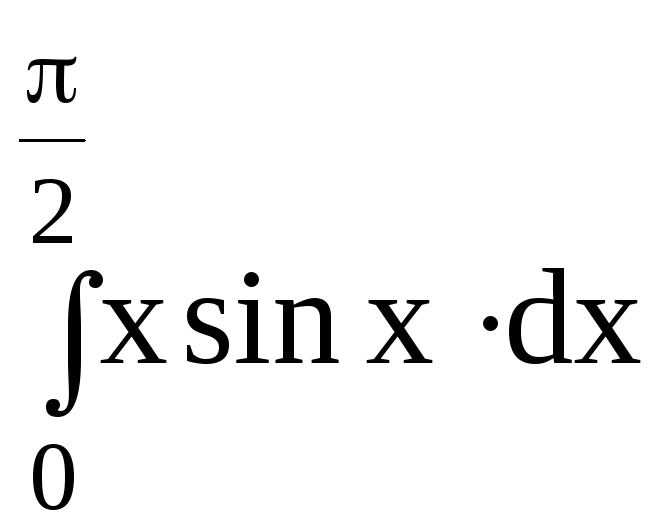
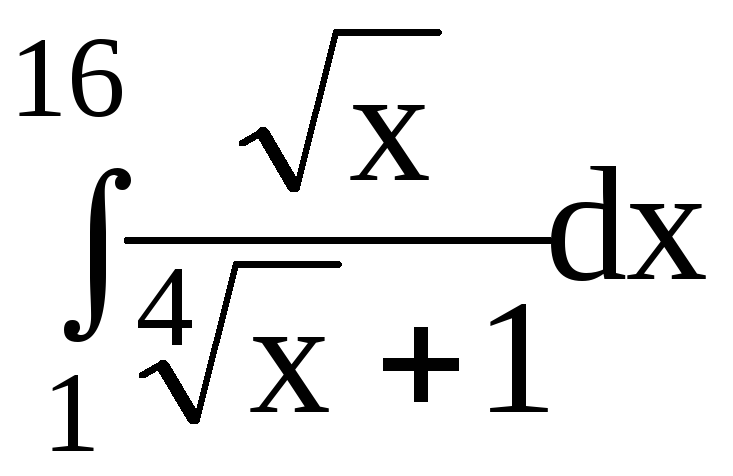
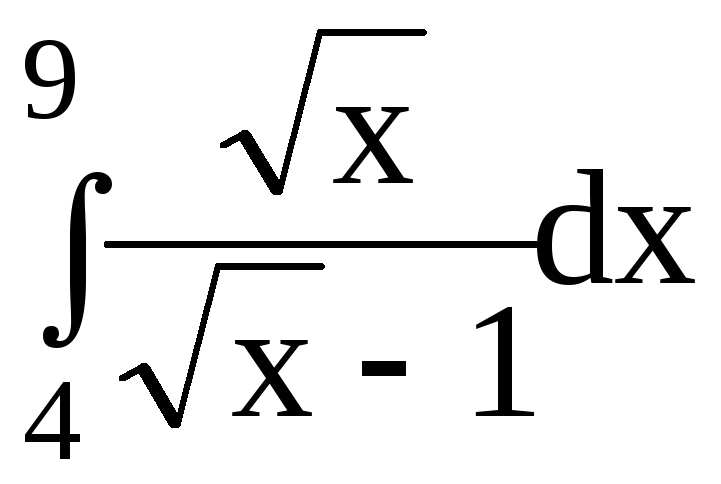
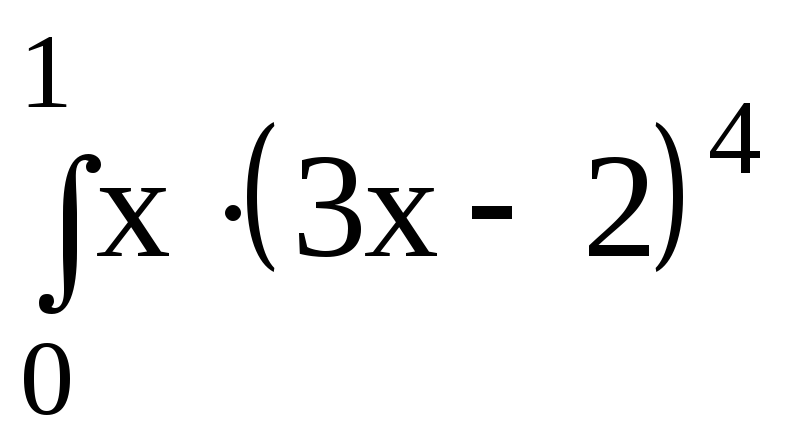 dx
dx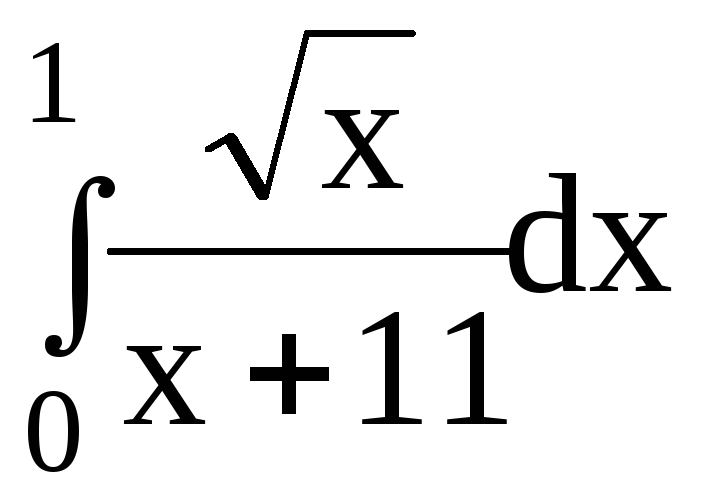
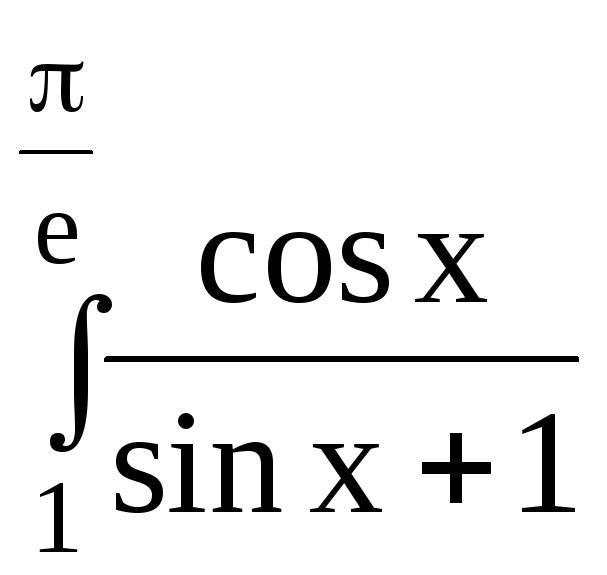 dx
dx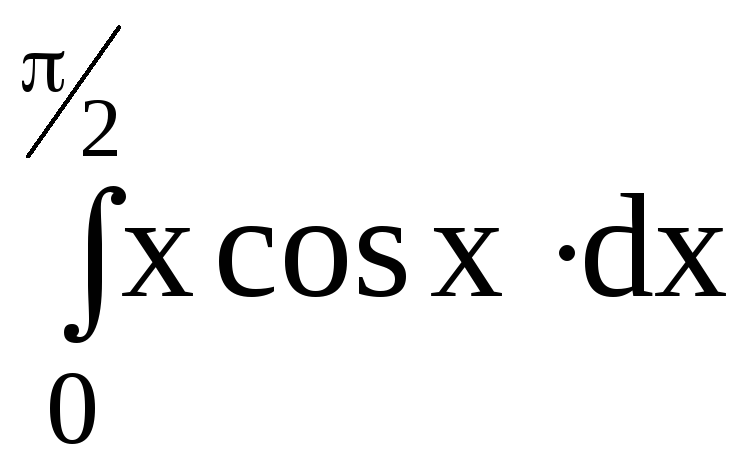
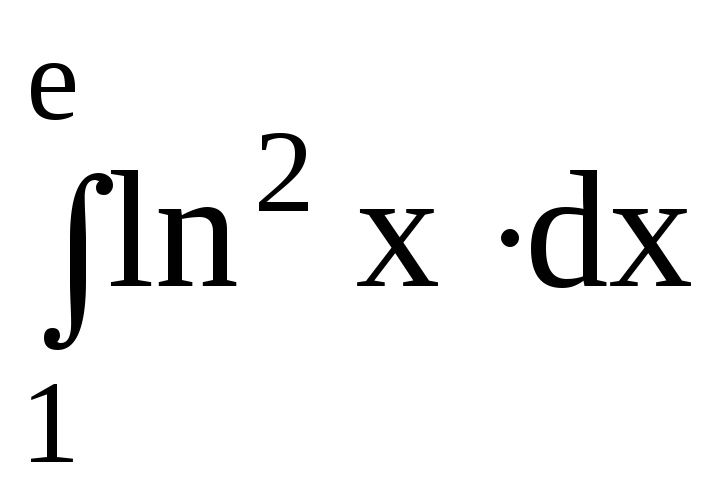
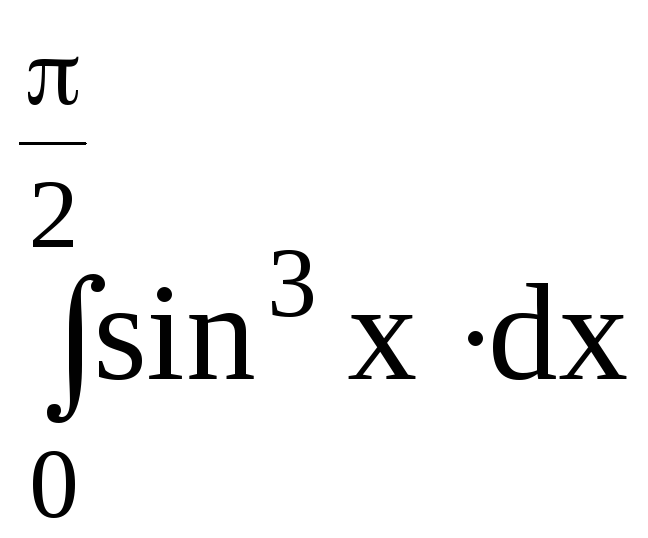
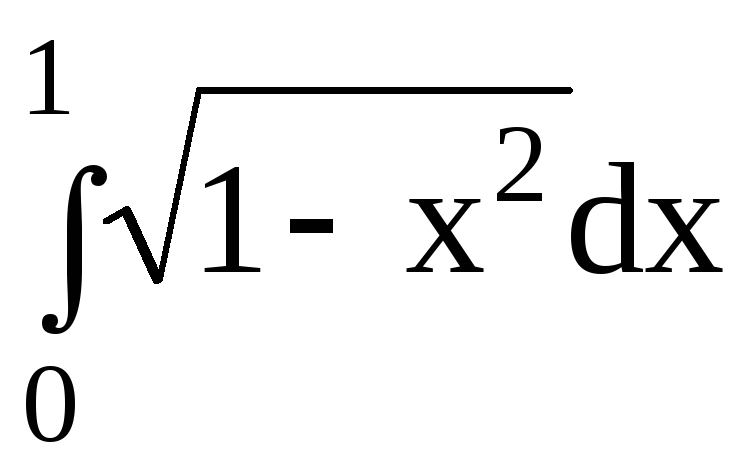
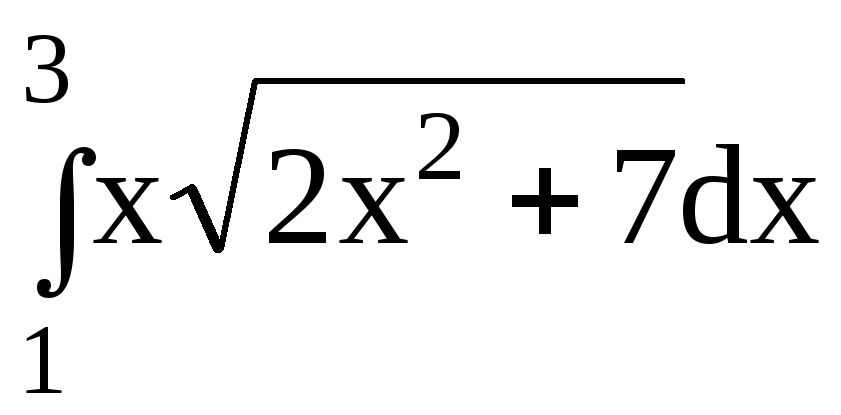
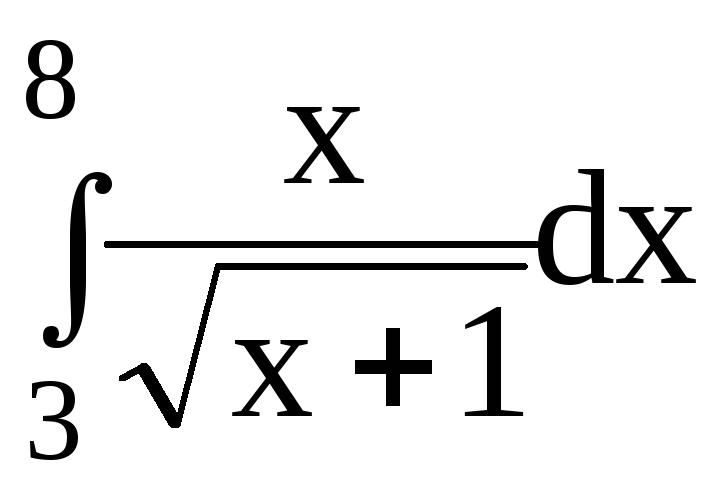
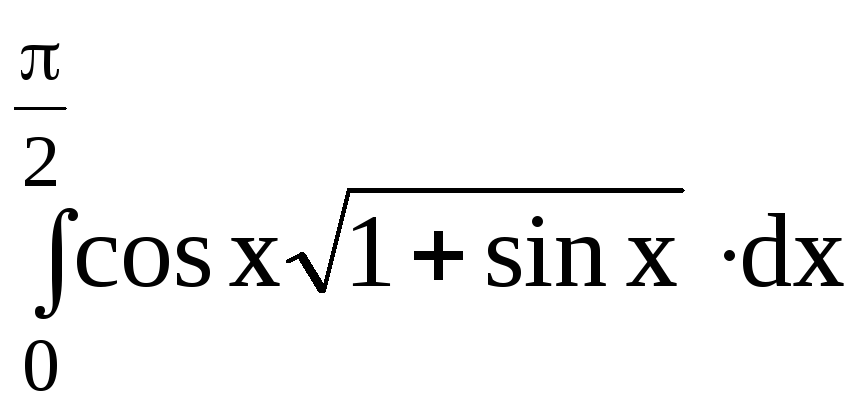
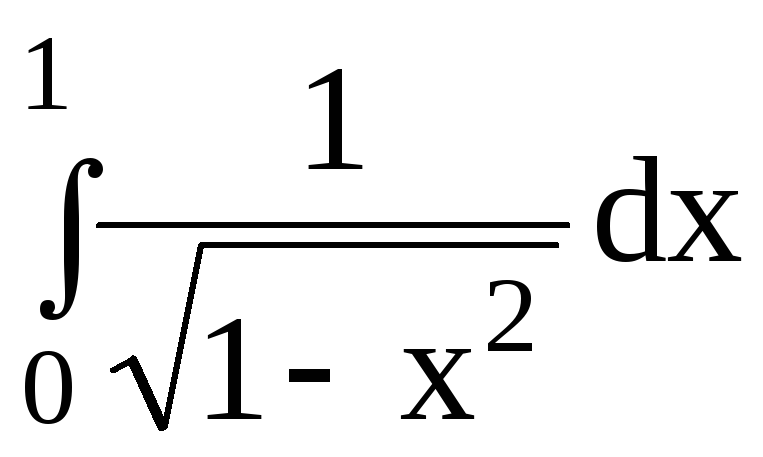
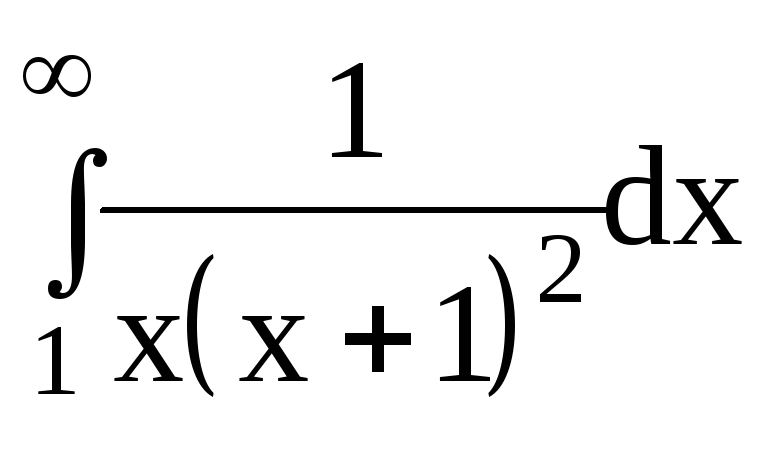
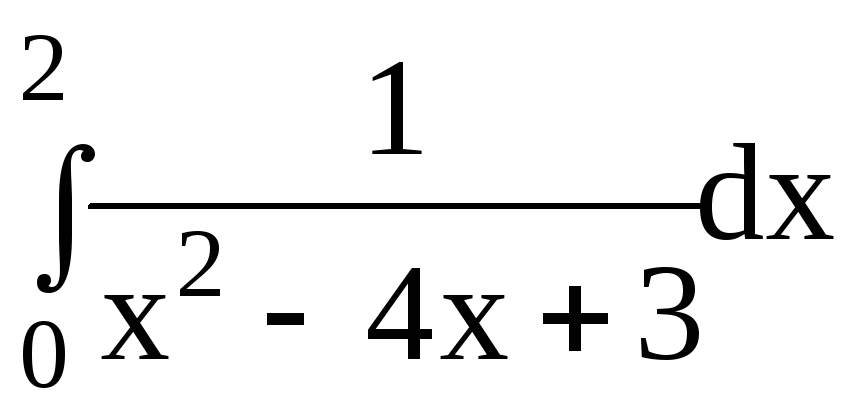

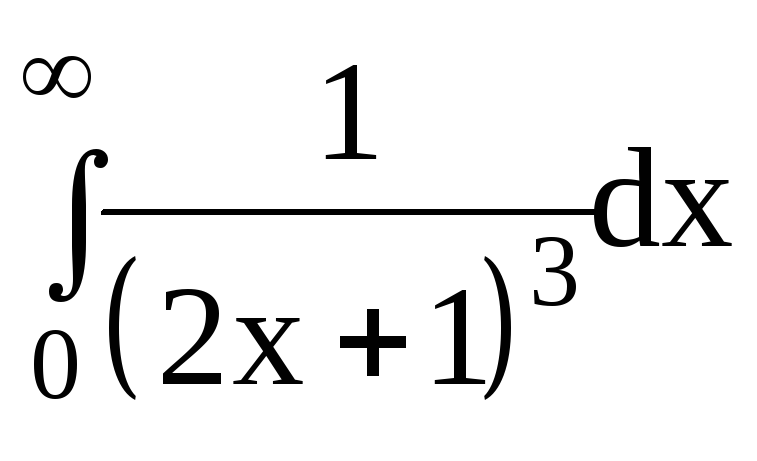
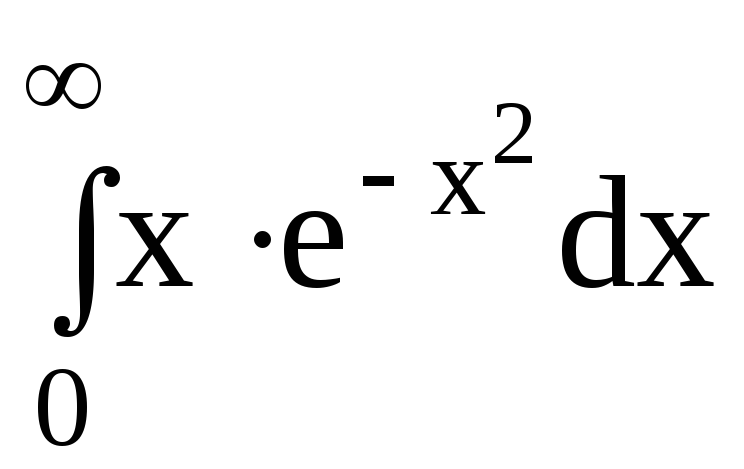
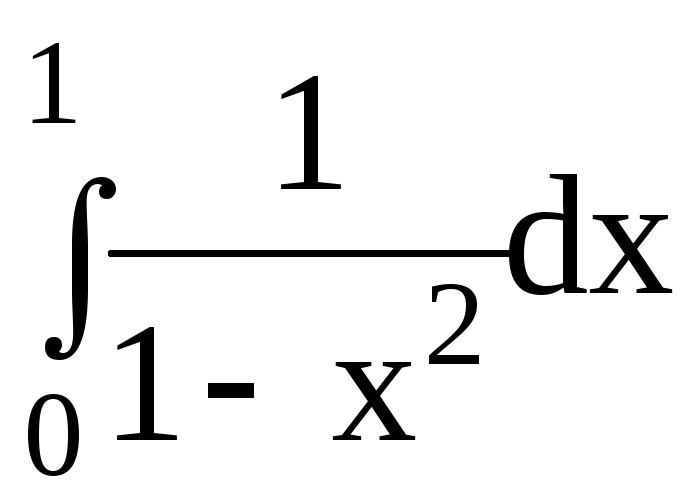
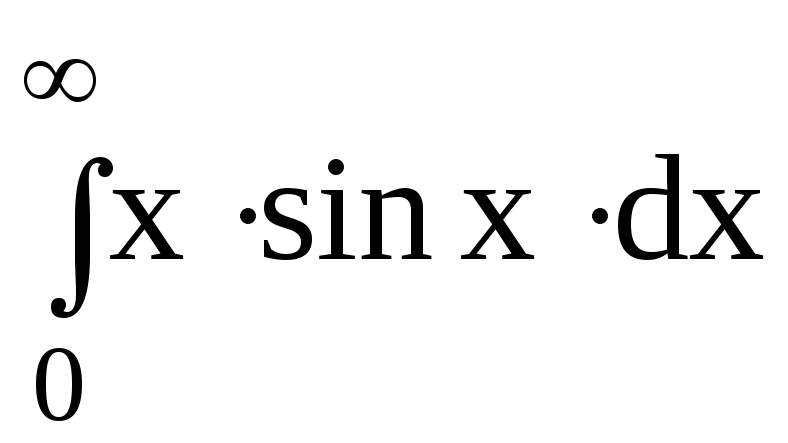
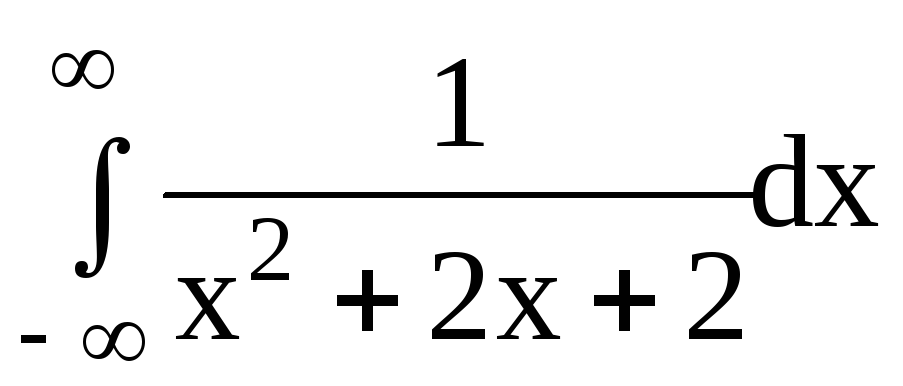
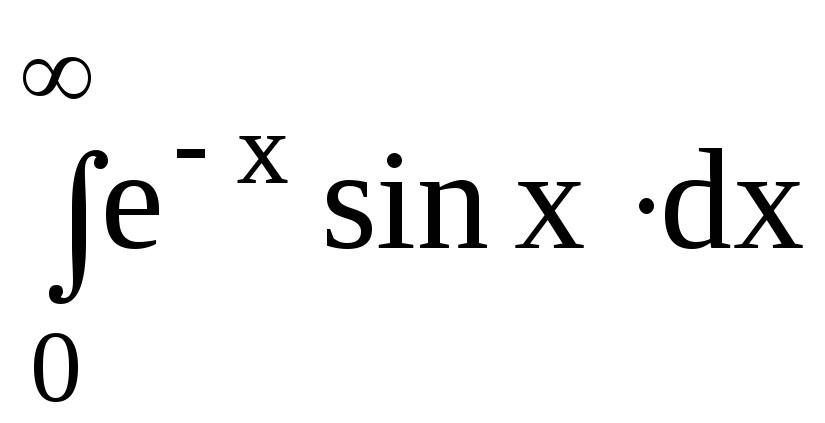
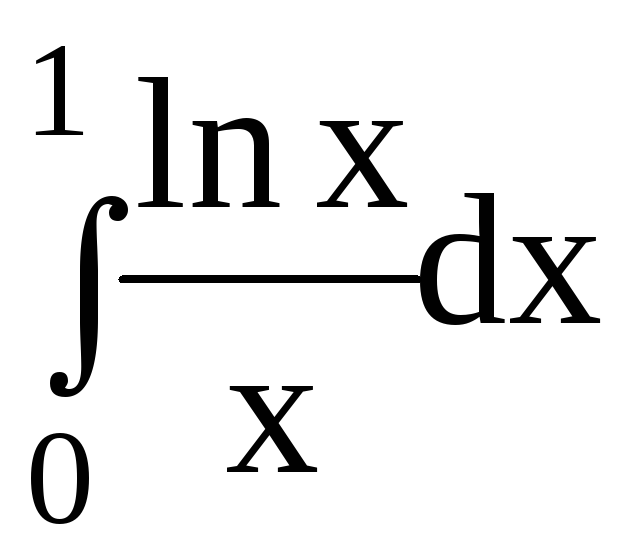

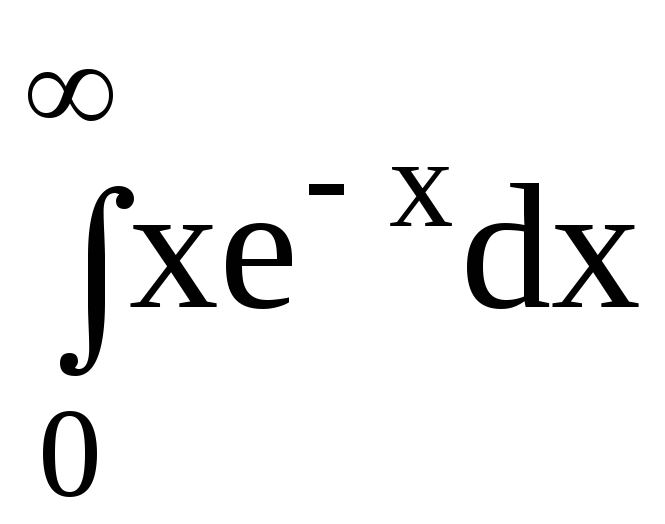
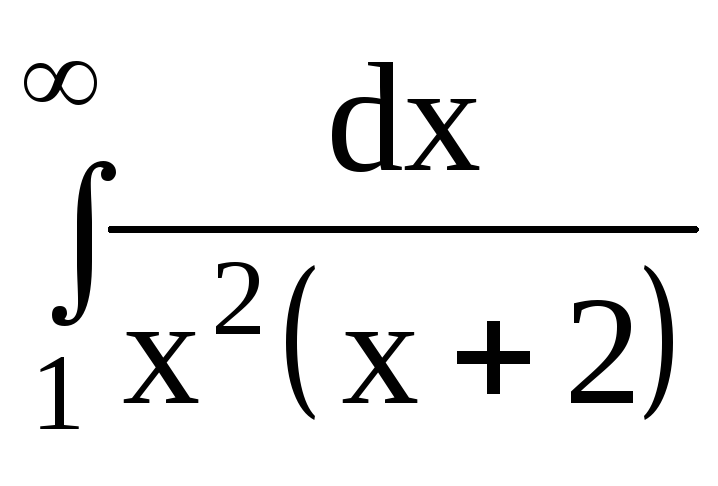


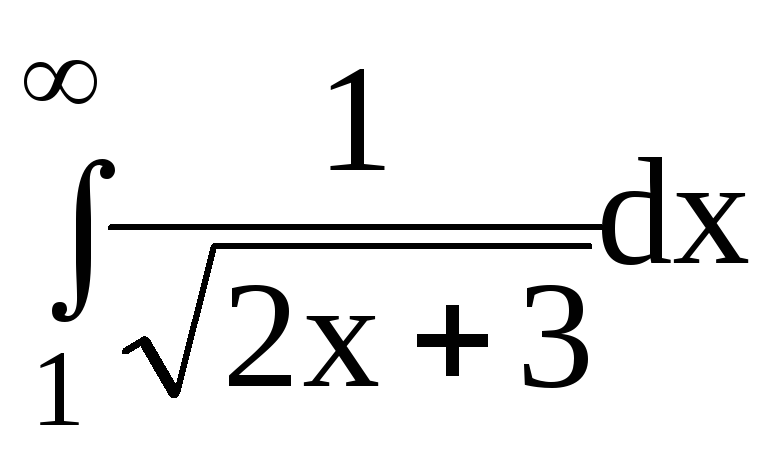

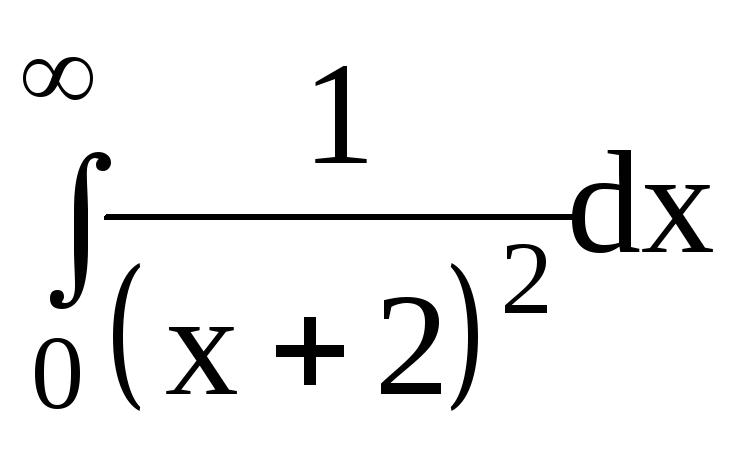
 dx
dx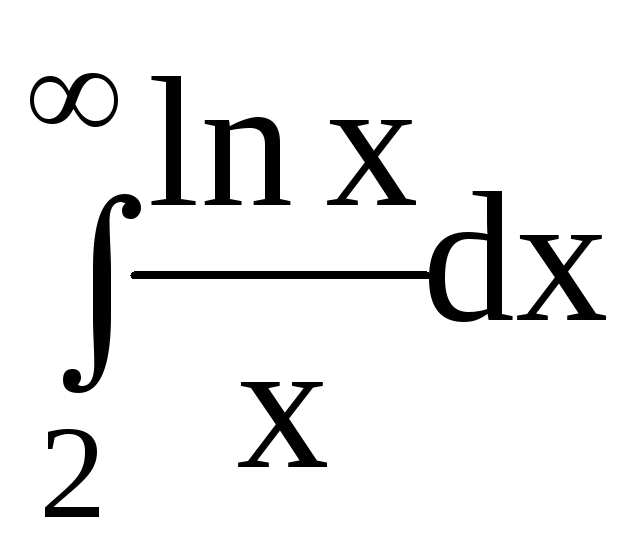

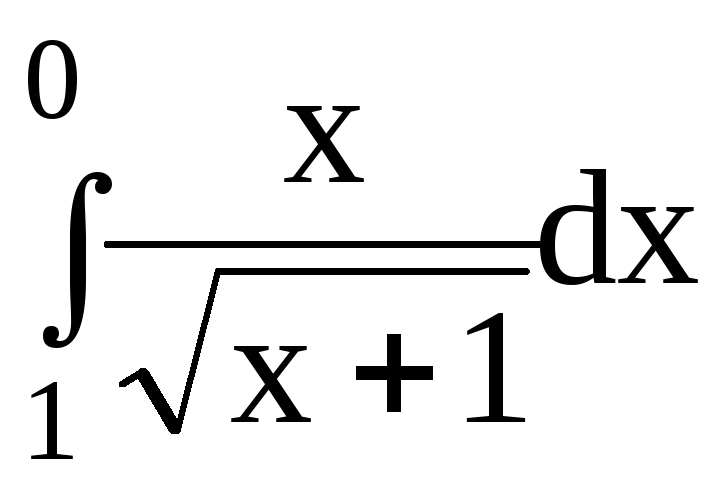

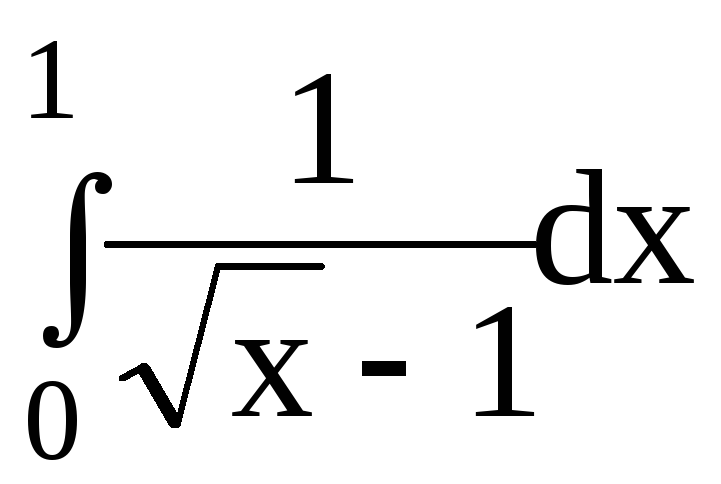
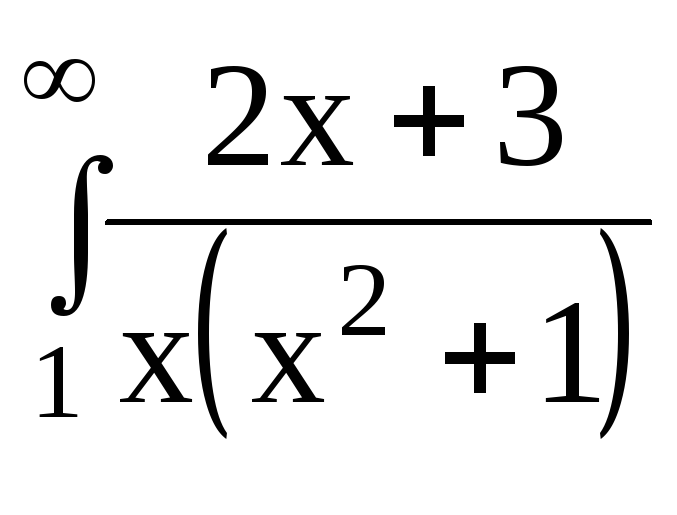 dx
dx