Порядок выполнения работы

1. Анализ схемы

Рассчитайте цепь, изображённую на рис.2.2.

Для этого по указанию преподавателя выберите её вариант (значения R₁ иR₅-R₈), обозначьте токи(I₁-I₅) и произвольно выберите их направления, составьте систему уравнений для цепи, используя первый и второй законы Кирхгофа. Решите полученную систему уравнений. Значения токов занесите в таблицу 2.1 в колонку «Расчёт».

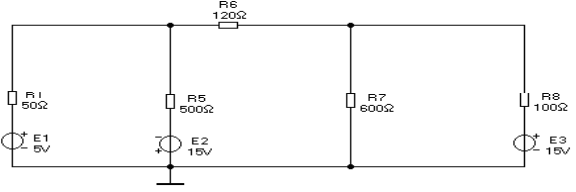
Рис.2.2. Разветвлённая цепь постоянного тока с тремя источником ЭДС

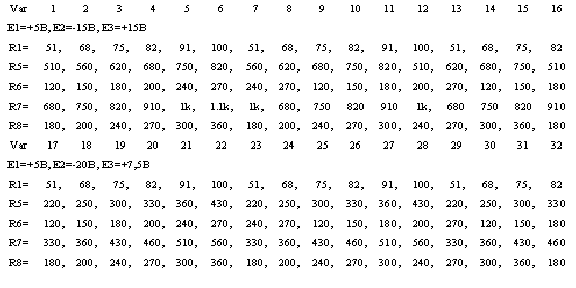Таблица 2.1

R1= R5= R6= R7= R8=	Расчёт					Моделирование
	I1 mA	I2 mA	I3 mA	I4 mA	I5 mA	I1 mA	I2 mA	I3 mA	I4 mA	I5 mA
Значения токов

2. Моделирование схемы

Включите компьютер и установите в нём программу моделирования электронных схемEWB.

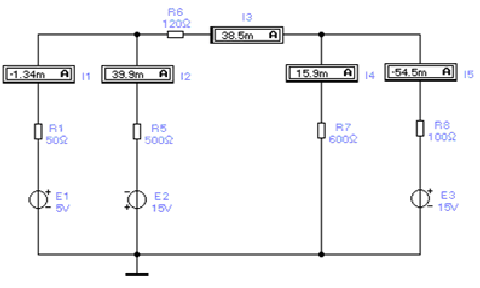
Рис.2.3. Модель разветвлённой цепи постоянного тока

Соберите на электронном столе схему, приведённую на рис.2.3, с номиналами резисторов для вашего варианта (аналог схемы, приведённой на рис.2.2). Включите схему и занесите все измеренные значения в таблицу 2.1 в колонку «Моделирование».

ОТЧЕТ

Лабораторная работа №3: Исследование разветвлённой электрической цепи постоянного тока и её расчёт методом контурных токов

Цель работы: теоретический расчёт методом контурных токов и моделирование разветвлённой электрической цепи постоянного тока.

Теоретические сведения

Метод контурных токовнапоминает метод расчета с использованием законов Кирхгофа, однако он несколько проще и поэтому получил большее распространение на практике при расчетах многоконтурных цепей, состоящих изnнезависимых контуров. Определение токов в ветвях сводится к решению системыn=m-(k-1)уравнений для контурных токовI_1k, I_2k, I_3k… действительный же ток в каждой ветви находится как алгебраическая сумма контурных токов, протекающих через соответствующую ветвь. Выбор направлений контурных токов произволен, но желательно, чтобы они имели одинаковые направления (тогда можно воспользоваться канонической системой уравнений). Каждая из ветвей сложной электрической цепи должна войти хотя бы в один из анализируемых контуров.

Каноническая система уравнений для независимых контуров имеет вид:

+R₁₁ I_1k-R₁₂I_2k- R₁₃I_3k- R₁₄I_4k-…=E₁₁;

-R₂₁ I_1k+R₂₂I_2k- R₂₃I_3k- R₂₄I_4k-…=E₂₂;

-R₃₁ I_1k-R₂₂I_2k+ R₃₃I_3k- R₃₄I_4k-…=E₃₃; и т.д.

Здесь R_ii (R₁₁, R₂₂ …)- сумма всех сопротивлений, по которым протекает рассматриваемый контурный токI_ik;

R_ij (R₁₂, R₂₁, R₁₃, R₃₁ …)- сумма сопротивлений, по которым одновременно протекаютI_ikиI_jkконтурные токи;

E_ii (E₁₁, E₂₂ …)– алгебраическая сумма ЭДС, имеющихся в рассматриваемом контуре.

Для иллюстрации рассматриваемого метода расчета обратимся к схеме на рис.3.1, на которой выбранные направления контурных токов обозначены стрелками, токи в ветвях контуров — расположением входных зажимов амперметров (утолщённая чёрная линия обозначает отрицательную клемму).

+R₁₁ I_1k-R₁₂I_2k- R₁₃I_3k=E₁₁;

-R₂₁ I_1k+R₂₂I_2k- R₂₃I_3k=E₂₂;

-R₃₁ I_1k-R₃₂I_2k+ R₃₃I_3k=E₃₃.

Здесь R₁₁= R₁+R₂; R₂₂= R₂+R₅+R₄; R₃₃= R₆+R₄;

R₁₂= R₂₁= R₂; R₁₃= R₃₁=0; R₂₃= R₃₂= R₄;

E₁₁= E₁-E₂-E₃; E₂₂= E₂-E₄; E₃₃=E₃+E₄.

После подстановки числовых значений получим:

20I_1k – 10I_2k = 60;

-10I_1k +22 I_2k -7I_3k=24;

-7I_2k + 22I_3k= 16.

Решив эту систему уравнений, найдем контурные токи:

I_1k =5А, I_2k =4А, I_3k = -2А.

Теперь найдем истинные токи во всех ветвях. В ветви, где действует ЭДС Е₁, истинный токI₁имеет направление контурного токаI_1k; и равен ему:I₁=I_1k= 5 А.В ветви с сопротивлениемR₅истинный токI₅имеет направление контурного токаI_1k и равен ему;I₅=I_1k =4A. В ветви с сопротивлениемR₆ истинный токI₆ имеют направление, противоположное контурному токуI_3k, и равенI₆= -I_3k =2 A. В ветви с сопротивлениемR₂истинный токI₂получится наложением контурных токовI_1kиI_2kи будет иметь направление большего из них, т.е.I₂ = I_1k - I_2k =1 А. В ветви с сопротивлениемR₄истинный токI₄ получится наложением контурных токовI_2kиI_3kи будет иметь направление большего из них, т.е.I₄ = I_2k – I_3k = 4+(-2)=2 А.

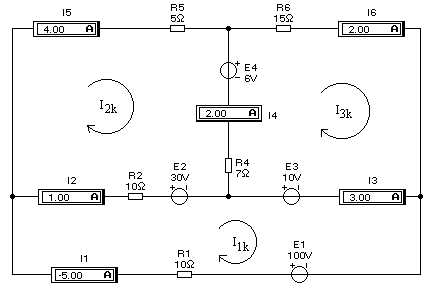
Рис. 3.1. Схема сложной трехконтурной цепи

В ветви, где действует ЭДС Е₃, истинный токI₃получится наложением контурных токовI_1kиI_3k, и будет иметь направление токаI_1k, т.е.I₃= I_1k – I_3k =5+(-2)=3 А. Из сравнения полученных расчетных данных с показаниями приборов на рис. 3.1 видно, что они полностью совпадают.