6

1 курс (ЭЖД)

ЛЕКЦИЯ 6 РЕШЕНИЕ ПРИКЛАДНЫХ ЗАДАЧ

2 семестр

6.1. Типовые алгоритмы

Пример 1. Вычисление суммы последовательности чисел, заданных общей формулой.

Составить программу для вычисления суммы:

Решение:

Const

N=17;

var

i:Integer;

s:Real;

begin

s:=0;

for i:=1 to N do s:=s+(2*i+1)/(i*i+2);

Writeln(' s = ',s:13:7);

Readln

end.

Сумма чисел, заданных общей формулой, вычисляется в цикле путем накопление результата в переменой s. Перед тем, как реализовать цикл, задается начальное значение суммы, равное нулю.

Пример 2. Вычисление значений функции на отрезке (табулирование функции).

Задана функция:

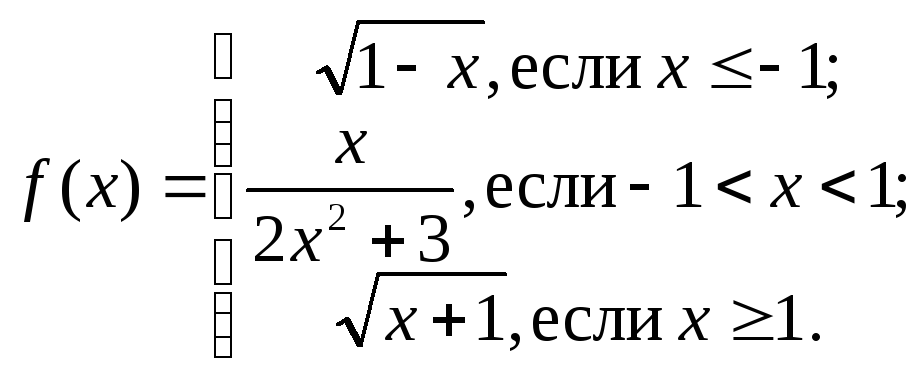
Составить программу для вычисления значений функции f(x) на отрезке [-3;4] с шагом x=0,3.

Решение:

var

xn,xk,h,x,y:Real;

begin {Начало головной программы}

Readln(xn,xk,h);

x:=xn;

while x<=xk do

begin

if x<=-1 then y:=Sqrt(1-x);

if Abs(x)<1 then y:=x/(2*x*x+3);

if x>=1 then y:=Sqrt(x+1);

Writeln(' x = ',x:12:6,' f(x) = ',y:12:6);

x:=x+h

end;

Readln

end.

Табулирование функции непосредственно реализовано с помощью оператора цикла с предусловием. Функция, как видно из постановки задачи, задана тремя ветвями: на интервале от – до –1 она принимает значения выражения ; на интервале [–1;1] – значения выражения ; и, наконец, на интервале от 1 до + – значения выражения . Вычисление значений функции во всех трех ветвях реализовано с использованием трех условных операторов IF в сокращенной форме IF...THEN.... Вычисление значений аргумента осуществляется так. Сначала задается его начальное значение (x:=xn), затем в конце цикла значение x каждый раз изменяется, увеличиваясь на шаг h. Вычисленные аргумент x и значение функции y выводятся на экран.

Пример 3 (вариант примера 1). Вычисление суммы элементов массива.

Задан одномерный массив действительных чисел a_k, k = 1,2, …, 20. Составить программу для вычисления суммы

.

Решение:

Const N=20;

var

k:Integer;s:Real;

a:array[1..N] of Real;

begin

for k:=1 to N do Read(a[k]);Readln;

s:=0;for k:=1 to N do s:=s+a[k];

Writeln(' s = ',s:13:7);

Readln

end.

Массив описан в разделе VAR. Элементы массива вводятся с помощью клавиатуры в одной строке, отделяются друг от друга пробелами. В конце ввода следует нажать [Enter]. Сумма вычисляется с помощью оператора цикла с параметром; ее начальное значение, равное нулю, задается до выполнения цикла, затем в цикле, как и в предыдущем примере производится ее накопление.

Пример 4. Вычисление среднего геометрического положительных элементов одномерного массива.

Задан одномерный массив a_k, k = 1,2, …, 25. Вычислить

.

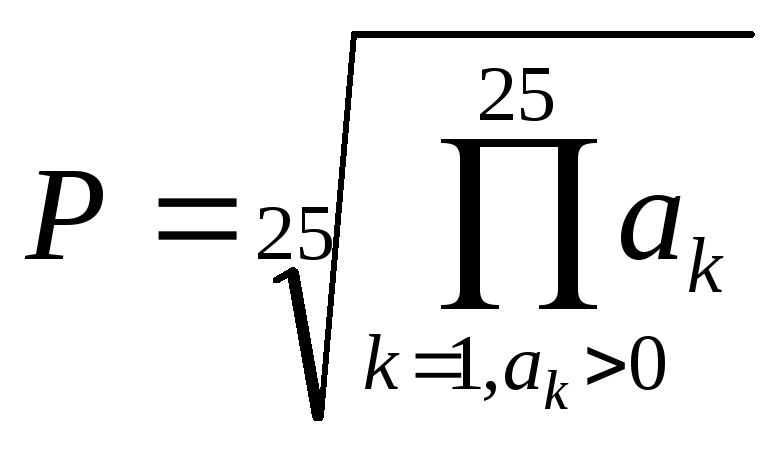Решение:

Const N=25;

var

k,m:Integer;p:Real;

a:array[1..N] of Real;

begin

for k:=1 to N do Read(a[k]);Readln;

p:=1;m:=0;

for k:=1 to N do

if a[k]>0 then begin p:=p+a[k];m:=m+1;end;

if m<>0 then Writeln(' p = ',Exp(Ln(p)/m):13:7)

else Writeln('No solve');

Readln

end.

Известно, что среднее геометрическое равно корню степени m из произведения заданных чисел, где m – количество этих чисел. Параметр m вначале задан равным нулю (в предположении, что положительных элементов в массиве может не быть). В программе выполняется проверка на положительность очередного элемента: если текущий элемент больше нуля, то, во-первых, выполняется умножение и, во-вторых, увеличение величины m на единицу (так как увеличилось на единицу число положительных элементов массива). Но, поскольку положительных элементов в массиве может не оказаться вообще, после завершения оператора цикла параметр m останется, равным нулю. В данном случае задача решений не имеет, что и должна вывести программа. Если же окажется, что этот параметр отличен от нуля, то задача имеет решение. Так как операция "возведение в степень" в языке Object Pascal отсутствует, ее придется заменить на некоторое выражение (в каждом конкретном случае – свое), связывающее экспоненту и логарифм (по определению логарифма ), что и реализовано в программе.

Пример 5. Нахождение наименьшего (наибольшего) элемента в массиве.

Задан одномерный массив a_k, k = 1,2, …, 15. Найти

.

Решение:

Const N=15;

var

k:Integer;min:Real;

a:array[1..N] of Real;

begin

for k:=1 to N do Read(a[k]);Readln;

min:=a[1];

for k:=2 to N do

if a[k]<min then min:=a[k];

Writeln(' min = ',min:10:4);Readln

end.

В данной программе реализован так называемый метод "пузырька". Сначала предполагается, что наименьшим элементом является первый элемент в массиве. Затем в цикле выполняется проверка. Если очередной элемент меньше текущего минимального, то последнему присваивается значение этого элемента, в противном случае ничего не выполняется.

6.2. Примеры программ

Пример 1. Линейная программа.

{$APPTYPE CONSOLE}

uses

SysUtils;

var

a,b,x1,x2,x3,x5,x6:Integer;x4:Real;

begin

Readln(a,b);

x1:=a+b;

x2:=a-b;

x3:=a*b;

x4:=a/b;

x5:=a div b;

x6:=a mod b;

Writeln(' x1 = ',x1,' x2 = ',x2,' x3 = ',x3);

Writeln(' x4 = ',x4:12:6);

Writeln(' x5 = ',x5,' x6 = ',x6);

Readln

end.

Данная программа демонстрирует выполнение арифметических операций над целочисленными операндами.

В этой программе единственная переменная x4 имеет вещественный тип, так как частное от "обычного" деления целого числа на целое всегда имеет вещественный тип.

В конце программы стоит вызов процедуры Readln, которая приостанавливает выполнение программы до нажатия клавиши [Enter]. Это сделано для того, чтобы дать возможность просмотреть результаты программы до ее завершения. Аналогично с этой же целью такой же процедурой будут заканчиваться и программы, приведенные в остальных примерах.

Пример 2. Решение квадратных уравнений.

Составить программу для вычисления корней квадратного уравнения:

.

Решение:

{$APPTYPE CONSOLE}

uses

SysUtils;

var

a,b,c,x1,x2:Real;

err:Boolean;

procedure QuadroRoots(a,b,c:Real;var x1,x2:Real;

var err:Boolean);

var d:real;

begin

err:=True;d:=b*b-4*a*c;

if d<0

then err:=False

else

begin

x1:=(-b-Sqrt(d))/2/a;x2:=-b/a-x1

end

end;

begin {Начало головной программы}

Readln(a,b,c);

QuadroRoots(a,b,c,x1,x2,err);

if err

then Writeln(' x1 = ',x1:12:6,' x2 = ',x2:12:6)

else Writeln(' This equation has no roots');

Readln

end.

Квадратное уравнение, как известно, полностью определяется своими коэффициентами a, b и c, которые и являются исходными данными. Основные вычисления оформлены в виде процедуры с тремя входными (a, b и c) и тремя выходными (x1, x2 и err) параметрами. Параметр err имеет булевский тип; если его значение равно True, то уравнение имеет действительные корни, которые и выводятся на экран. В противном случае программа выводит на экран только сообщение о том, что уравнение не имеет действительных корней.