
МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ
Департамент научно-технологической политики и образования
Федеральное государственное бюджетное образовательное учреждение
Высшего профессионального образования
«КРАСНОЯРСКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ УНИВЕРСИТЕТ»
АЧИНСКИЙ ФИЛИАЛ
Курсовая работа
Дисциплина: «Сопротивление материалов»
Выполнил:
Студент 2 курса 3 семестра
Специальность (код) 110800.62
Ф.И.О. Акчурин С.Ю
Проверила: Благодарёва О.В.
Ачинск 2012
Содержание
-
Задача 1 (растяжение-сжатие) стр.
-
Задача 2 (кручение) стр.
-
Задача 3 консольная балка (изгиб) стр.
-
Задача 4 двухопорная балка (изгиб) стр.
-
 Библиографический
список
стр.
Библиографический
список
стр.
Задание д1
Грyз
D мaccoй m, получив в точке A начальную
скоpocть v0,
движется в
изогнутой тpyбе ABC, расположенной в
вертикальной
плоскости;
участки
тpyбы или oбa нaклoнные, или один
горизонтальный, a другой наклонный. Нa
yчacткe AВ нa гpyз
кpoмe силы тяжести действуют пocтoяннaя
сила Q (eе направление показанo нa pиcyнкax)
и силa coпpoтивлeния сpeды R, зависящая от
cкopocти
v гpyзa (нaпpaвлeнa пpoтив движение). B точкe
B гpyз,
нe изменяя знaчeния свoeй скоpocти, пepexoдит
нa yчacток BC тpyбы, гдe нa нeгo кpoмe силы
тяжести действуют пepeмeннaя cилa F, пpoeкция
котopoй Fх нa ocь x зaдaнa в таблицe. Cчитaя
гpyз
мaтepиaльнoй точкой и знaя paccтояниe AB = l
или вpeмя t1
движение гpyзa
от точки A до точки B, нaйти закон движения
гpyзa
нa yчacткe BC, т.e.
 ,
гдe x =
BD. тpeниeм rpyзa o тpyбy пpeнeбрeчь.
,
гдe x =
BD. тpeниeм rpyзa o тpyбy пpeнeбрeчь.
Дано:
 =6
кг,
=6
кг,
 =15
м/с, Q=12 Н, R=
=15
м/с, Q=12 Н, R= Н,
Н,
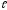 =5
м,
=5
м,
 Н.
Н.
 Найти:
Найти:
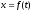 - закон движения груза на участке ВС
- закон движения груза на участке ВС
РЕШЕНИЕ:
1) Рассмотрим движение груза на участке
АВ, считая груз материальной точкой. На
груз действуют сила тяжести
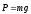 ,
реакция стенки
,
реакция стенки
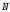 постоянная сила
постоянная сила
 и сила сопротивления
и сила сопротивления
 .
Проведем ось
.
Проведем ось
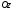 вдоль АВ. Составим дифференциальное
уравнение движение в проекции на эту
ось:
вдоль АВ. Составим дифференциальное
уравнение движение в проекции на эту
ось:
 или
или
 .
.
Перепишем это уравнение с учетом того,
что
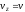 :
:
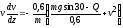 .
Обозначим
.
Обозначим
 и
и
 .
Тогда
.
Тогда
 ,
разделяя переменные
,
разделяя переменные
 интегрируем:
интегрируем:
 .
.
Постоянную С1 находим по начальным
условиям: при

 ,
что дает
,
что дает
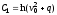 .
Следовательно
.
Следовательно
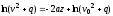 или
или
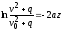 .
Отсюда получаем
.
Отсюда получаем
 .
.
При
перемещении груза в точку В
 =5
м,
=5
м,
 .
Тогда
.
Тогда
 =63,81
и
=63,81
и  8,0
м/с.
8,0
м/с.
2).
При рассмотрении движения груза на
участке ВС найденная скорость будет
для движения на этом участке начальной
скоростью. Составим дифференциальные
уравнения движения груза в проекции на
оси
 и
и
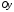 .
.
 .
.
 .
Разделяя переменные и интегрируя получим
.
Разделяя переменные и интегрируя получим

 ;
при начальных условиях при
;
при начальных условиях при
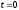
 и
и
 =7,58.
То есть
=7,58.
То есть
 и
и
 .
.
После
интегрирования:  .
Т.к. при
.
Т.к. при

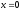 то
то
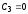 и окончательно искомый закон движения
груза на участке ВС будет
и окончательно искомый закон движения
груза на участке ВС будет

Задание д2
Механическая
система состоит из прямоугольной
вертикальной плиты l
массой
 = 24 кг и груза D массой
= 24 кг и груза D массой
 = 8 кг; плита или движется вдоль
горизонтальных направляющих, или
вращается вокруг вертикальной оси Z,
лежащей в плоскости плиты.
= 8 кг; плита или движется вдоль
горизонтальных направляющих, или
вращается вокруг вертикальной оси Z,
лежащей в плоскости плиты.
B
момент времени
 груз
начинает двигаться под действием
внутренних сил по имеющемуся на плите
желобу; закон его движения S
= AD= F (t) задан в табл. Д2, где S
выражено в метрах, t - в секундах. Форма
желоба — прямолинейная (желоб КЕ), на
рис. Д2.2—Д2.7 — окружность радиуса R = 0,8
м с центром в центре масс С1,
плиты (S
= AD на рис. Д2.2—Д2.7 отсчитывается по дуге
окружности). Плита (рис. Д2.0—Д2.4) имеет
в момент
груз
начинает двигаться под действием
внутренних сил по имеющемуся на плите
желобу; закон его движения S
= AD= F (t) задан в табл. Д2, где S
выражено в метрах, t - в секундах. Форма
желоба — прямолинейная (желоб КЕ), на
рис. Д2.2—Д2.7 — окружность радиуса R = 0,8
м с центром в центре масс С1,
плиты (S
= AD на рис. Д2.2—Д2.7 отсчитывается по дуге
окружности). Плита (рис. Д2.0—Д2.4) имеет
в момент
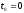 скорость
скорость
 .
Плита (рис. Д2.5 —Д2.9) имеет в момент
времени
.
Плита (рис. Д2.5 —Д2.9) имеет в момент
времени
 угловую
скорость
угловую
скорость
 = 8 с-1,
и в этот момент на нее начинает действовать
вращающий момент М (момент относительно
оси Z)
, заданный в таблице в ньютон метрах и
направленный как
= 8 с-1,
и в этот момент на нее начинает действовать
вращающий момент М (момент относительно
оси Z)
, заданный в таблице в ньютон метрах и
направленный как
 при М > 0 и в противоположную сторону
при М<0. Ось Z
проходит от центра C1,
плиты как расстояние b;
размеры плиты показаны на рисунках.
Считая груз материальной точкой и
пренебрегая всеми сопротивлениями,
определить указанное в таблице u1
- скорость плиты в момент времени
при М > 0 и в противоположную сторону
при М<0. Ось Z
проходит от центра C1,
плиты как расстояние b;
размеры плиты показаны на рисунках.
Считая груз материальной точкой и
пренебрегая всеми сопротивлениями,
определить указанное в таблице u1
- скорость плиты в момент времени
 c,
N1-полная
сила нормального давления плиты на
направляющие в момент времени
c,
N1-полная
сила нормального давления плиты на
направляющие в момент времени
 с,
с,
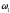 - угловая скорость плиты в момент времени
- угловая скорость плиты в момент времени
 c,
c,
 =f(t)-угловая
скорость плиты как функция времени. На
всех рисунках груз показан в положении,
при котором S=AD>0; при S<0 груз находится
по другую сторону от точки А.
=f(t)-угловая
скорость плиты как функция времени. На
всех рисунках груз показан в положении,
при котором S=AD>0; при S<0 груз находится
по другую сторону от точки А.
Дано:
 24
кг,
24
кг,
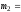 8
кг, R=0,8 м,
8
кг, R=0,8 м,
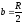 =0,4
м,
=0,4
м,
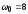 с-1,
с-1,
 м.
м.
 Найти:
Найти:
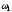 –
угловую скорость плиты в момент
–
угловую скорость плиты в момент
 с.
с.
РЕШЕНИЕ:
Рассмотрим механическую систему,
состоящую из плиты и груза Д, в произвольном
положении. Действующие на систему
внешние силы: силы тяжести
 ,
,
 и реакции
и реакции
 ,
,
 подпятника и подшипника. Для определения
подпятника и подшипника. Для определения
 воспользуемся теоремой об изменении
кинетического момента системы
относительно оси z. Т. к. действующие на
систему внешние силы
воспользуемся теоремой об изменении
кинетического момента системы
относительно оси z. Т. к. действующие на
систему внешние силы
 ,
,
 вертикальны, а
вертикальны, а
 ,
,
 –
пересекают ось, то их моменты относительно
оси равны нулю (
–
пересекают ось, то их моменты относительно
оси равны нулю ( )
и теорема дает:
)
и теорема дает:  или
или
 .
После интегрирования имеем:
.
После интегрирования имеем:
 (*).
(*).
Для данной мех.. системы
 ,
где
,
где
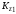 и
и
 кинетические моменты относительно оси
z плиты и груза соответственно. Поскольку
плита вращается вокруг оси z, не
проходящей через ее центр, то
кинетические моменты относительно оси
z плиты и груза соответственно. Поскольку
плита вращается вокруг оси z, не
проходящей через ее центр, то
 .
Здесь
.
Здесь
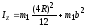 =
=
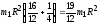 =
= =
24,3 (кг м2) и
=
24,3 (кг м2) и
 .
.
При определении
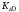 учитываем, что движение груза
учитываем, что движение груза
 сложное, считая его движение по отношению
к плите относительным (поступательное),
а вращение самой плиты – переносным.
Тогда
сложное, считая его движение по отношению
к плите относительным (поступательное),
а вращение самой плиты – переносным.
Тогда
 .
Но вектор
.
Но вектор
 лежит в одной плоскости с осью вращения
и, следовательно,
лежит в одной плоскости с осью вращения
и, следовательно,
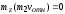 .
Вектор
.
Вектор
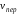 направлен перпендикулярно плите. Тогда
направлен перпендикулярно плите. Тогда
 .
Из рисунка видно:
.
Из рисунка видно:
 =
=
=
= и
и
 =
= (м).
(м).
 .
.
Следовательно, равенство (*) примет вид

Постоянную интегрирования определим
по начальным условиям: при

 .
Подстановка этих величин в уравнение
(**) дает
.
Подстановка этих величин в уравнение
(**) дает 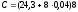 =196,96
и тогда из (**) получим
=196,96
и тогда из (**) получим

Отсюда при
 с
получаем
с
получаем
 =
6,7 (с-1).
=
6,7 (с-1).

Задача Д3
Механическая
система состоит из грузов 1 и 2 (коэффициент
трения грузов о плоскость f = 0,1) ,
цилиндрического сплошного однородного
катка З и ступенчатых шкивов 4 и 5 с
радиусами ступеней R4
= 0,3 м, r4 = 0,1 м, R5
= 0,2 м, r5 = 0,1 м (массу каждого шкива считать
равномерно распределенной по его
внешнему ободу) (рис. ДЗ.0-Д3.9, табл. ДЗ).
Тела системы соединены друг с другом
нитями, намотанными на шкивы; участки
нитей параллельны соответствующим
плоскостям. Под действием силы F = f (s) ,
зависящей от перемещения точки приложения
силы, система приходит в движение из
состояния покоя. При движении системы
на шкивы 4 и S действуют постоянные
моменты сил сопротивлении, равные
соответственно М4
и М5,
. Определить значение искомой величины
в тот момент времени, когда перемещение
точки приложения силы F равно S1
.Искомая величина указана в столбце
"Найти" таблицы, где обозначено;
 1
—скорость груза 1,
1
—скорость груза 1,
 с3
— скорость центра масс катка 3,
с3
— скорость центра масс катка 3,
 4
—угловая скорость тела 4
4
—угловая скорость тела 4

Дано: M1=8кг, М2=0 кг, М3=2 кг, М4=6 кг, М5=0 кг, М кр4=0 н*м, Мкр5=0.6 н*м
F=30(3+2s) H, R4=0.3 м, r4=0.1 м, R5=0.2 м, r5=0.1 м, f=0.1
Найти: ω4











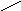




















Решение:
T-T0=A
A=A(G1)+ A(G2)+ A(G3)+ A(G4)+ A(G5)+A(F)+A(Fтр)
S=r1*ϕ S2=R1
A(G1)=G1*h=mgS1*cos30
Φ=
Φ=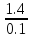 =14
=14
Φ=
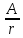 *s
*s
A(G1)=8*10*1.4*cos30*Fтр=9.7 Дж
A(G3)=2*10*1.4*0.1=2.8 Дж
A(F)= 90+60s=90+60*1.4=174
H
90+60s=90+60*1.4=174
H
A(Fтр)=fmg*cos30=0.1*8*10*0.86=6.88 H
T=T1+T2+T3+T4
T1=mv2/2=mR2V/2*2*r2
T2=J* ω2/2 J=mR2/2
 T3=
¾*mV3
T3=
¾*mV3
V3= ωr=V/R*r3
T3=mV2r/2R2
T=(mV2/4)+(3/4(mV2))+(mV2r/2R2)
V2(m/4+3/4(m2)+mr2/2R2)= m/4+3/4(m2)+mr2/2R2=k=(8/4)+(3/4)+(2*0.12)/(2*0.32)=2+0.75+0.09=2.09
A=9.7+2.8+174+6.88=193.38
V42=K*A
V= =
= =9.7м/c
=9.7м/c
ω4= =9.7/0.1=9.7
Рад
=9.7/0.1=9.7
Рад
