3. Цифровые логические элементы

Простейшие логические элементы обычно реализуют стандартные логические функции от одной или нескольких переменных. На схемах они изображаются как показано на рис. 3.1 и называются по имени соответствующей функции.

С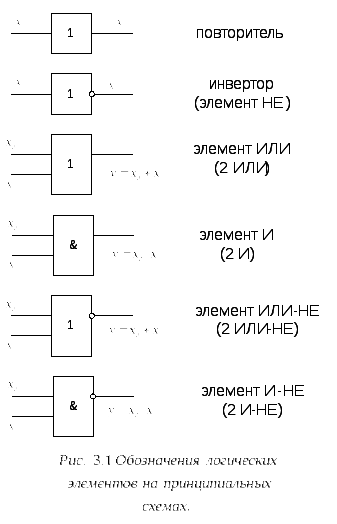уществует лишь две разновидности одновходовых логических элементов. Один из них не меняет значения входной переменной и называется повторителем, или буферным элементом, а другой – инвертор реализует функцию отрицания -НЕ. Он формирует выходной сигнал, являющийся инверсией входного.

Работу логических элементов как и свойства логических функций, удобно описывать с помощью таблиц. Для двухвходовых элементов ИЛИ и ИЛИ-НЕ они представлены на рис. 3,2.

Из анализа таблиц вытекает, что функцию ИЛИ можно представить проинвертировав выходной сигнал элемента ИЛИ-НЕ. Схемотехнически это можно реализовать как показано на рис 3.3.

Рассмотрим, что произойдет, если соединить входы у двухвходовых элементов (рис. 3.4). При этом на оба входа будет подаваться одинаковый сигнал. Воспользовавшись правилами алгебры логики, получим,,. Таким образом, элементы2И и 2ИЛИ будут выполнять функции буферных, а 2И-НЕ, 2ИЛИ-НЕ - инверторов.

Из действующих в алгебре логики законов Де-Моргана (3.1) следует, что инверсия логического произведения переменных равна логической сумме их инверсий, а инверсия суммы есть произведение инверсий переменных.

(3.1)

Из этих соотношений вытекает, что любую логическую функцию, содержащую и произведения и суммы, можно представить лишь через две операции - сложение и инверсию (ИЛИ и НЕ) либо умножение и инверсию (И и НЕ). Для технической реализации представленных таким образом функций могут быть использованы однотипные логические элементы И-НЕ, либо ИЛИ-НЕ. Кроме того, из сочетательного закона алгебры логики следует, что, переменные можно обрабатывать не сразу, а по парам, расставляя, где надо в выражениях скобки.

К примеру, реализация функции потребует четырехвходового логического элемента ИЛИ. Однако, преобразовав ее к виду , либо , можно обойтись тремя двухвходовыми, соединив их как показано на рис.3.5.

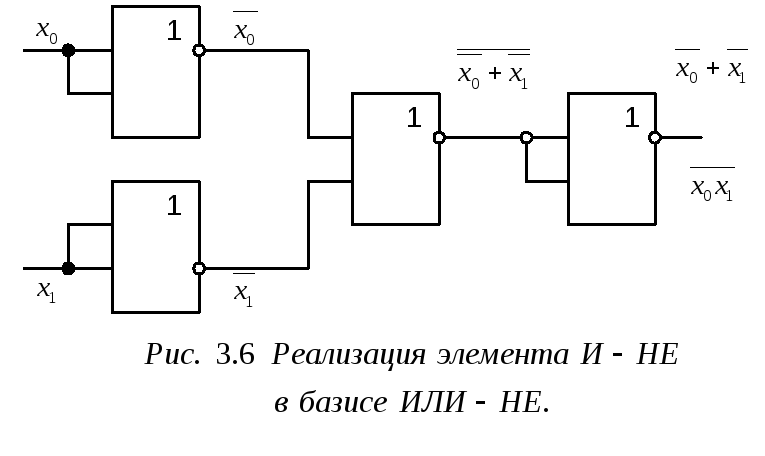
Следовательно, логическую функцию от любого количества переменных можно реализовать, используя лишь двухвходовые элементы, выполняющие операции 2И-НЕ, либо 2ИЛИ-НЕ. Поэтому элементы такого типа называются базисными или базовыми.

Р

ассмотрим, к примеру, как в базисеИЛИ-НЕ реализовать функцию И-НЕ для двух переменных и . Воспользовавшись правилами Де-Моргана, можно записать: , то есть, чтобы получить нужную функцию требуется проинвертировать входные переменные, а затем сложить их без инверсии, что реализуется при показанном на рис. 3.6 соединении элементов2ИЛИ-НЕ.

Аналогичным образом из однотипных элементов можно построить любое сколь угодно сложное цифровое устройство. Однако на практике на основе простейших логических элементов создают различные функционально-законченные узлы, используя которые строят цифровые системы.

В зависимости от схемотехнических решений базовым элементом серии может быть элемент И-НЕ, либо ИЛИ-НЕ. В то же время существуют серии микросхем, в которых достаточно просто удается создать любую требуемую конфигурацию и там базовый элемент выделить затруднительно.