
2 Основы квантовой физики
.pdf
на выбранное направление. Вычислить вероятность нахождения электрона в области от 0,9r0 до 1,1r0 при любых Θ.
Задача 100. (3) Найти среднее расстояние электрона, находящегося в основном состоянии в атоме водорода, от центра атома.
5. ТУННЕЛЬНЫЙ ЭФФЕКТ
Прохождение квантовой частицы из одной классически разрешенной для движения области в другую, когда частица преодолевает потенциальный барьер, называется туннельным эффектом. Это специфический квантовый эффект, не имеющий классического аналога. Наиболее интересной величиной здесь является коэффициент проницаемости барьера – вероятность того, что частица пройдет через барьер с одной попытки.
Для прямоугольного барьера шириной a и высотой Wb точное выражение для коэффициента проницаемости имеет вид:
|
|
2 |
k |
2 |
|
2 |
k |
2 |
|
2 |
sh |
2 |
2 |
k |
2 |
, |
(5.1) |
|
b 4kb |
|
kb |
|
|
|
kba 4kb |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где k |
2mW ; kb |
2m Wb W |
; W – полная энергия частицы. |
|
|||||||||||||
Если туннельный эффект существенно подбарьерный, т. е. в формуле (5.1) kba >> 1, то для вычисления коэффициента проницаемости прямоугольного барьера получается приближенное выражение:
|
b |
exp |
2 a |
2m W |
W . |
(5.2) |
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
Для барьера произвольной формы коэффициент проницаемости может быть оценен по приближенной формуле:
b exp |
2 |
x2 dx |
2m Wp x W |
, |
(5.3) |
|
|
x1 |
|
|
|
где x1 и x2 – классические точки остановки, т. е. точки входа под барьер и выхода из под него соответственно.
Массы некоторых частиц, необходимые для решения задач, приведены в прил. 3, табл. П.3.1.
31
Вопросы для самопроверки и задачи
1)Приведите примеры ядерно-физических явлений, объясняемых туннельным эффектом.
2)Изобразите на графике зависимость коэффициента проницаемости прямоугольного барьера от его толщины.
3)Изобразите на графике зависимость коэффициента проницаемости прямоугольного барьера от его высоты.
4)Проинтерпретируйте туннельный эффект с помощью соотношения неопределенностей для энергии и времени.
5)Приведите пример устройства, в котором туннельный эффект находит практическое применение.
Задача 101. (2) Вероятность прохождения нейтрона через прямоугольный барьер высотой 10 МэВ и шириной 10 фм составляет 1 %. Какова скорость этого нейтрона?
Задача 102. (3) Два электрона, имеющие энергию 3 эВ, проходят через прямоугольные потенциальные барьеры высотой 5 и 7 эВ и шириной 0,10 нм и 50 пм соответственно. Во сколько раз коэффициент проницаемости первого барьера больше коэффициента проницаемости второго?
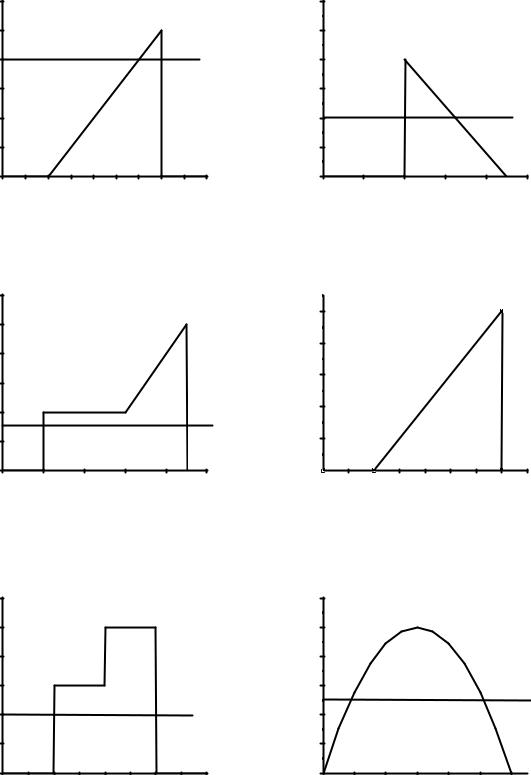
Задача 103. (2) Оценить коэффициент прохождения через барьер, изображенный на рис. 1, для электрона.
Задача 104. (3) Оценить коэффициент прозрачности барьера, изображенного на рис. 2, для позитрона.
Задача 105. (2) Оценить вероятность того, что электрон пройдет через барьер, изображенный на рис. 3.
Задача 106. (2) Оценить прозрачность барьера (рис. 4) для мюона. Задача 107. (2) Коэффициент прозрачности барьера, изображенного на
рис. 5, для протона равен 0,003. Каким импульсом обладает этот протон? Задача 108. (3) Оценить прозрачность барьера, изображенного на рис. 6,
для альфа-частицы.
Задача 109. (3) Как и во сколько раз изменится коэффициент прохождения барьера, изображенного на рис. 6, если альфа-частицу заменить на нестабильный изотоп гелий-6?
32
12 |
|
|
|
|
|
|
|
|
|
300 |
|
|
|
|
|
|
|
||
10 |
|
|
W |
|
|
|
|
|
250 |
|
|
|
|
|
|
|
|||
(x), эВ |
8 |
|
|
|
|
|
|
(x), кэВ |
200 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
6 |
|
|
|
|
|
|
|
|
150 |
|
W |
|
|
|
|
|
|||
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
4 |
|
|
|
|
|
|
|
|
p |
100 |
|
|
|
|
|
|
|||
W |
|
|
|
|
|
|
|
|
W |
|
|
|
|
|
|
|
|||
|
2 |
|
|
|
|
|
|
|
|
|
|
50 |
|
|
|
|
|
|
|
|
00 |
2 |
4 |
6 |
8 10 12 14 16 18 |
|
|
00 |
|
2 |
4 |
6 |
8 |
10 |
|||||
|
|
|
|
x, нм |
|
|
|
|
|
|
|
|
x, пм |
|
|
|
|||
|
|
|
|
Рис. 1 |
|
|
|
|
|
|
|
|
Рис. 4 |
|
|
||||
|
6 |
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
МэВ,(x) |
|
16 |
|
|
|
|
|
|
|
|
эВ,(x) |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W |
W |
|
|
|
|
|
|
|
W |
|
8 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
p |
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
00 |
|
2 |
4 |
6 |
8 |
|
10 |
|
|
00 |
2 |
4 |
6 |
8 |
10 12 14 16 |
|||
|
|
|
|
x, нм |
|
|
|
|
|
|
|
|
x, фм |
|
|
||||
|
|
|
|
Рис. 2 |
|
|
|
|
|
|
|
|
Рис. 5 |
|
|
||||
|
6 |
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
эВ |
5 |
|
|
|
|
|
|
|
|
МэВ |
|
10 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
(x), |
|
|
|
|
|
|
|
|
||
(x), |
3 |
W |
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
W |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
p |
2 |
|
|
|
|
|
|
|
p |
4 |
|
|
|
|
|
|
|
||
W |
|
|
|
|
|
|
|
|
W |
|
|
|
|
|
|
|
|
||
|
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
00 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
00 |
2 |
4 |
|
6 |
8 |
10 |
12 |
|
|
|
|
|
x, A |
|
|
|
|
|
|
|
|
|
|
x, фм |
|
|
|
|
|
|
|
Рис. 3 |
|
|
|
|
|
|
|
|
Рис. 6 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
33 |
|
|
|
|
|
|
|
|
|
Задача 110. (4) Среднее время жизни нестабильного изотопа гелий-8 составляет 119 мс. Сколько процентов ядер гелий-8 пройдет через барьер, изображенный на рис. 6, прежде чем вещество распадется?
Библиографический список
1.Трофимова Т. И. Курс физики / Т. И. Трофимова. М., 1997. 542 с.
2.Детлаф А. А. Курс физики / А. А. Детлаф, Б. М. Яворский.
М., 2000. 718 с.
3.Савельев И. В. Курс общей физики / И. В. Савельев. М., 1982. Т.
3.304 с.
4.Джанколи И. В. Физика / И. В. Джанколи. М., 1989. Т. 2. 667 с.
5.Нерсесов Э. А. Основные законы атомной и ядерной физики /
Э. А. Нерсесов. М., 1988. 288 с.
6.Гольдин Л.Л. Введение в квантовую физику / Л. Л. Гольдин,
Г. И. Новикова. М., 1988. 328 с.
7.Блохинцев Д. И. Основы квантовой механики / Д. И. Блохинцев.
М., 1976. 664 с.
8.Физический энциклопедический словарь. М., 1984. 944 с.
34

ПРИЛОЖЕНИЕ 1
Понятие о функции распределения
Для успешного изучения квантовой механики и последующих разделовкурса физики необходимо знание некоторых понятий и формул теории вероятности и математическойстатистики. Напомнимнекоторыеизних.
Функция распределения (плотность вероятности) f x некоторой случай-
ной физической величины X показывает, как часто величина X будет принимать значениявблизиx. Пояснимэтонапримере.
Часто поведение случайной величины описывается так называемой функцией распределенияГаусса:
fG x 2 2 12 e x 2 |
2 2 . |
(П.1.1) |
График функции (П.1.1) напоминает сечение колокольчика с максимумом при x = μ. Значит, значения x вблизи числа встречаются чаще (функция распределения вблизи этого значения велика), а чем дальше число x отстоит от , тем реже оно встречается. Именно «по Гауссу» распределены значения прямых измерений, получаемые при выполнении лабораторных работ. В квантовой физике под значением случайной величины часто понимают координату точки, в которой можетбытьобнаруженаквантоваячастица.
Математический смысл плотности вероятности (функции распределения) состоит в том, что через нее выражается малая вероятность dΠ найти частицу в
малом интервале dx вблизи заданной точки x (в интервале от x до x + dx): |
|
d f x dx . |
(П.1.2) |
Формулу (П.1.2) можно считать определением плотности вероятности, |
|
поскольку |
|
f x d |
(П.1.3) |
dx |
|
напоминает определение плотности в одномерном случае, например, линейной плотности заряда – отсюда и название – плотность вероятности.
Если известна функция распределения, то интегрированием формулы (П.1.2) на конечном интервале x1, x2 можно получить вероятность
35
x |
|
|
2 |
f x dx , |
(П.1.4) |
x1 |
|
|
с которой частицу можно обнаружить внутри этого интервала.
Как правило, функция распределения (плотность вероятности) удовле-
творяет условию нормировки:
|
f x dx 1, |
|
|
(П.1.5) |
смысл которого заключается в том, что вероятность обнаружить частицу на всей числовой оси равна единице.
Часто для расчета вероятности нахождения частицы в некотором интервале числовой оси удобно пользоваться функцией распределения вероятности:
F x x |
f x dx , |
(П.1.6) |
|
|
|
котораяпоказываетвероятностьтого, чточастицанаходится наосилевеечислаx. Тогда, очевидно, вероятностьобнаружитьчастицувинтервале x1, x2 :
F x2 F x1 . |
(П.1.7) |
Используя хорошо известную в математической статистике теорему о произведении вероятностей независимых событий, формулы (П.1.2) – (П.1.5)
можно распространить на двумерный или трехмерный случай.
Так, плотность вероятности f r в трехмерном случае определяет малую вероятность того, что частица будет обнаружена в малом объеме dV:
d f r dV. |
(П.1.8) |
Тогда формула (П.1.4) и условие нормировки (П.1.5) примут вид:
f r dV ; |
(П.1.9) |
|
|
V |
|
|
f r dV 1. |
(П.1.10) |
Вформуле (П.1.9) интегрирование ведется по интересующему объему пространства, а в формуле (П.1.10) – по всему пространству.
36
Элемент объема интегрирования dV в декартовых координатах, очевидно, определяется выражением:
dV dx dy dz , |
(П.1.11) |
а в сферических координатах –
dV r2 sin d d dr . (П.1.12)
Для систем, подчиняющихся статистическим закономерностям, функция распределения имеет важнейшее значение. Можно утверждать: если для статистической системы известна функция распределения, то для такой системы известно все. Подобно тому, как для механической системы знание радиуса- векто-ра позволяет найти все характеристики движения (скорость, ускорение и т. д.), для статистической системы знание функции распределения дает исчерпывающую информацию о такой системе. Следовательно, задача нахождения функции распределения – основная задача статистики. В разных разделах физики эта задача решается разными методами. Так, в статистической физике функция распределения часто находится из распределения Гиббса, в квантовой физике – из решения уравнения Шрёдингера.
Упражнение. Пусть плотность вероятности попадания фотонов на экран имеет вид гауссова распределения. Определить вероятность попадания фотонов в интервал x 0,3 ; 0,3 .
ПРИЛОЖЕНИЕ 2
Уравнение Шрёдингера
Поведение квантовой частицы не может быть описано с помощью классических величин, таких как радиус-вектор r t и импульс p t . Не «работает»
в квантовом мире и второй закон Ньютона. На смену ему приходит уравнение Шрёдингера (Нобелевская премия 1933 г.), которое для одномерной системы имеет вид:
i |
x, t |
|
2 |
|
2 x, t |
W |
x x, t . |
(П.2.1) |
t |
2m |
|
x2 |
|||||
|
|
|
p |
|
|
В уравнении Шрёдингера внешними факторами, влияющими на его решение, являются две величины: масса квантовой частицы и вид потенциальной
37

ямы, в которой эта частица находится. Вид потенциальной ямы задается потенциальной функцией Wp x , которая определяет зависимость потенциальной
энергии частицы от ее координаты. Неизвестной в этом уравнении является функция координаты и времени Ψ(x, t), которая называется волновой функцией. Смысл волновой функции как решения уравнения Шрёдингера заключается в том, что волновая функция позволяет вычислить плотность вероятности:
f x, t |
|
x, t |
|
2 . |
(П.2.2) |
|
|
||||
Волновую функцию как решение уравнения Шрёдингера в рассматривае- |
|||||
мом случае можно представить в виде: |
|
||||
x, t (x)e iWt , |
(П.2.3) |
||||
разделяя тем самым координатную и временнýю зависимости волновой функции. Подставляя выражение (П.2.4) в уравнение Шрёдингера, легко получить так называемое уравнение Шрёдингера для стационарных состояний:
d 2 x |
|
2m |
W W |
x x 0 |
, |
(П.2.4) |
||
dx2 |
2 |
|||||||
|
|
p |
|
|
|
|||
решением которого являются волновые функции, зависящие только от координат. Смысл волновой функции (амплитуды вероятности) как решения уравнения Шрёдингера заключается в том, что квадрат модуля волновой функции равен плотности вероятности (функции распределения), характеризующей распределение вероятности обнаружения частицы в различных участках числовой оси:
f x |
|
x |
|
2 . |
(П.2.5) |
|
|
Упражнение. Доказать, что если Wp(x) – потенциальная энергия, зависящая только от координат, то выражение (П.2.3) является решением уравнения
Шрёдингера (П.2.1), и что справедливо равенство x 2 x, t 2 .
38
ПРИЛОЖЕНИЕ 3
Справочные сведения
Таблица П.3.1 Некоторые физические постоянные
Постоянная |
Значение |
|
|
Скорость света, м/с |
2,99792458·108 |
Элементарный заряд, Кл |
1,6021773·10–19 |
Масса покоя электрона и позитрона, кг |
9,1093898·10–31 |
Масса покоя протона, кг |
1,6726231·10–27 |
Масса покоя нейтрона, кг |
1,6749286·10–27 |
Постоянная Планка h, Дж · с |
6,6260755·10–34 |
Постоянная Планка ħ, Дж · с |
1,0545727·10–34 |
Постоянная Больцмана, Дж / К |
1,3806581·10–23 |
Постоянная Ридберга, м–1 |
1,0973731·107 |
Таблица П.3.2 Работа выхода электронов из некоторых металлов
Металл |
Работа выхода, эВ |
Металл |
Работа выхода, эВ |
|
|
|
|
Алюминий |
4,2 |
Натрий |
2,3 |
Барий |
2,4 |
Никель |
4,5 |
Вольфрам |
4,5 |
Платина |
5,3 |
Калий |
2,2 |
Рубидий |
2,2 |
Литий |
2,4 |
Серебро |
4,3 |
Медь |
4,4 |
Цезий |
1,8 |
Молибден |
4,3 |
Цинк |
4,0 |
|
|
|
|
39
Учебное издание
ГОНЧАР Игорь Иванович, ЛИТНЕВСКИЙ Леонид Аркадьевич
ОСНОВЫ КВАНТОВОЙ ФИЗИКИ В ЗАДАЧАХ
––––––––––––––––––
Редактор Т. С. Паршикова
***
Подписано в печать .02.2008. Формат 60 × 84 1/16. Плоская печать. Бумага офсетная. Усл. печ. л. 2,5. Уч.-изд. л. 2,7.
Тираж 1000 экз. Заказ .
**
Редакционно-издательский отдел ОмГУПСа Типография ОмГУПСа
*
644046, г. Омск, пр. Маркса, 35
40
