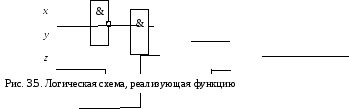
- •2.1. Логические схемы и логические функции
- •2.2. Переход от логической схемы к формуле логической функции
- •2.3. Переход от алгоритма работы к логической схеме
- •3. Применение алгебры логики
- •3.1. Решение текстовых логических задач
- •3.1.1. Методика решения логических задач
- •3.1.2. Примеры
- •3.2. Применение логических операций при решении задач на эвм
- •3.2.1. Примеры
- •3.3. Преобразование логических выражений и схем
- •3.3.1. Примеры
3.3.1. Примеры
Пример 3.6. Упростить
логическое выражение:
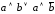 .
.
По закону дистрибутивности вынесем a за скобки:
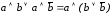 .
.
По закону исключенного третьего скобочное выражение заменяем логической константой 1:
 .
.
Используем закон исключения констант:
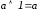 .
.
Пример 3.7. Упростить
логическое выражение:
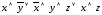 .
.
Введем вспомогательный
логический множитель
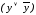 :
:
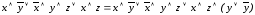 .
.
На основании дистрибутивного закона раскрываем скобки и комбинируем (в соответствии с переместительным законом) два крайних и два средних логических слагаемых:
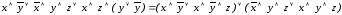
Используем закон поглощения:
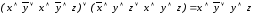 .
.
Пример 3.8. Требуется
упростить:
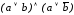 .
.
Способ 1. Применим закон дистрибутивности:
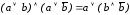 .
.
К выражению в скобках применим закон противоречия:
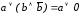 .
.
Применим закон исключения констант:
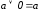 .
.
Способ 2. Перемножим скобки (как в обычной алгебре чисел) на основании дистрибутивного закона:
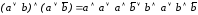 .
.
К логическому слагаемому применим закон идемпотентности, потом два средних слагаемых сгруппируем и общий логический множитель вынесем за скобки, заменим последнее слагаемое (на основании закона противоречия) логической константой 0:
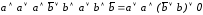 .
.
Используем законы исключенного третьего и исключения констант:
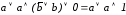 .
.
Используем закон исключения констант:
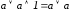 .
.
Применяем закон идемпотентности
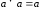 .
.
Пример 3.9.
Упростить ЛС из примера 2.1 (рис. 2.2).
Логическое выражение, описывающее ЛС,
имеет вид:
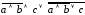 .
.
Применим ко второму слагаемому закон де Моргана:
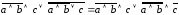 .
.
Применяем закон двойного отрицания:
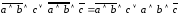 .
.
Последнее выражение
это неравнозначность относительно
логических выражений
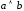 и
и .
Поэтому имеем:
.
Поэтому имеем:
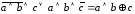 .
.
Осталось нарисовать ЛС.
Пример 3.10. Составить логическую схему, реализующую логическую функцию f(x, y, z), заданную таблицей истинности (табл. 3.5).
|
Таблица 3.5 | |||
|
Таблица f(x, y, z) | |||
|
x |
y |
z |
f |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
1 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
0 |
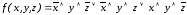 .
.
Замечание 3.5. Последнее выражение называется совершенной дизъюнктивной нормальной формой (СДНФ).
Полученное выражение
можно упростить. Для этого сгруппируем
первые два слагаемых и вынесем множитель
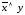 за скобки:
за скобки:
 .
.
Применяя законы исключенного третьего и исключения констант, имеем:
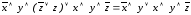 .
.
Вынесем логический множитель y за скобки, а к скобочному выражению применим дистрибутивный закон:
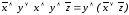 .
.
Применяя закон де Моргана имеем:
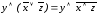 .
.
Получилась очень простая логическая схема (рис. 3.5):