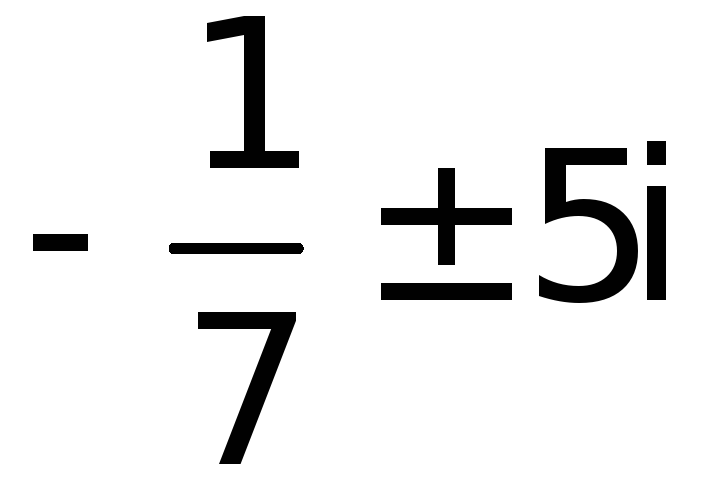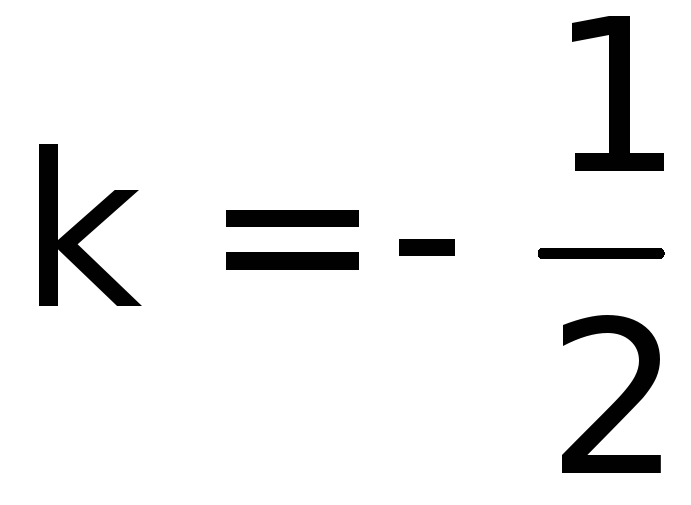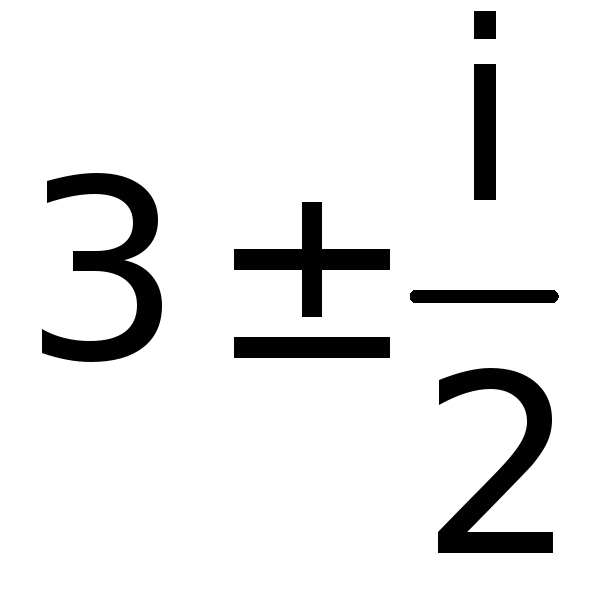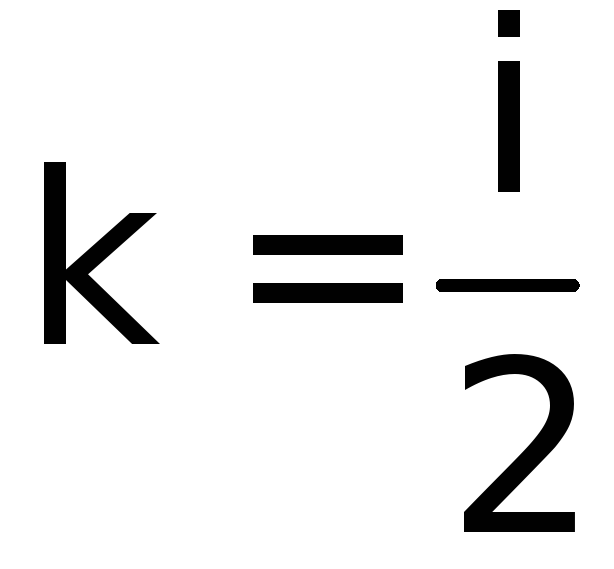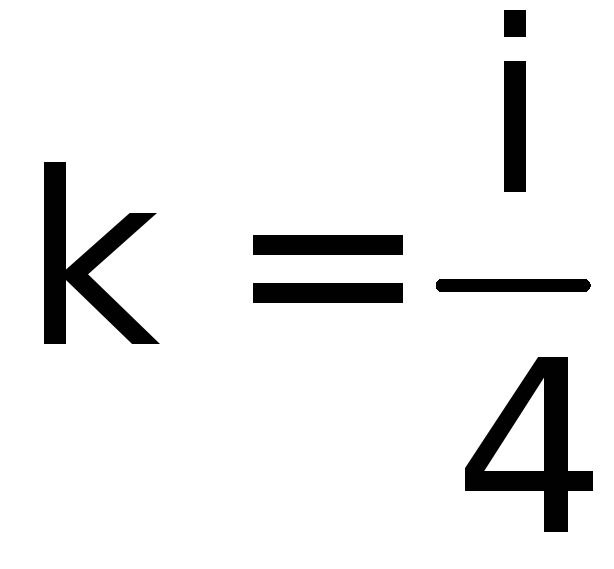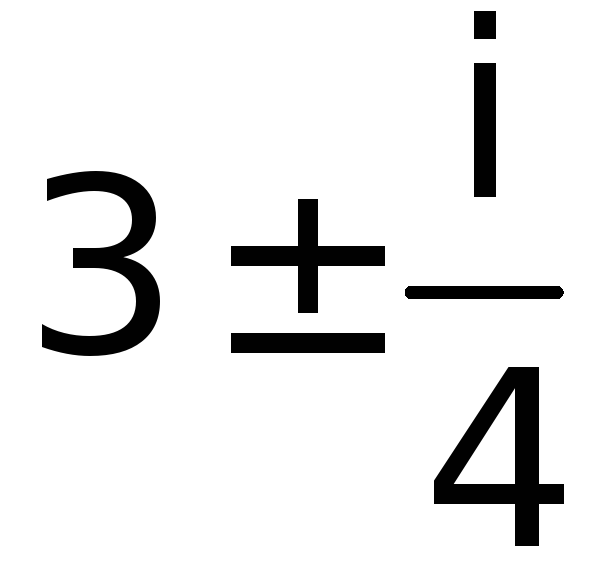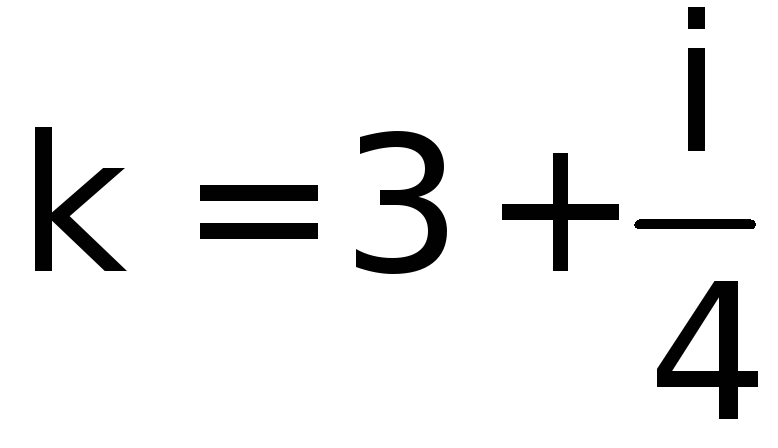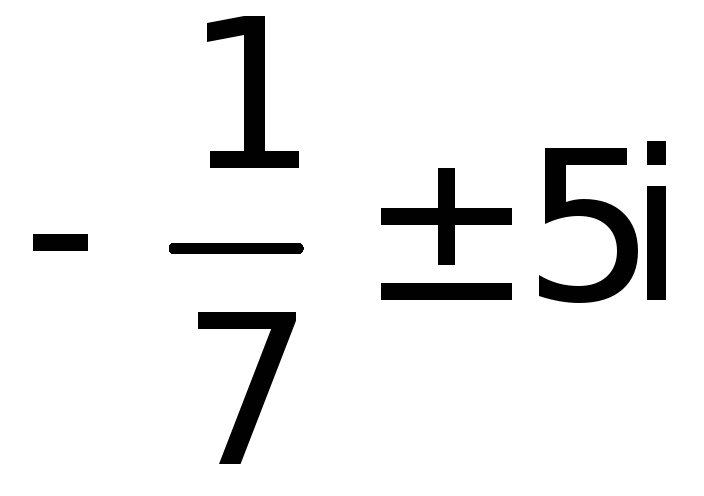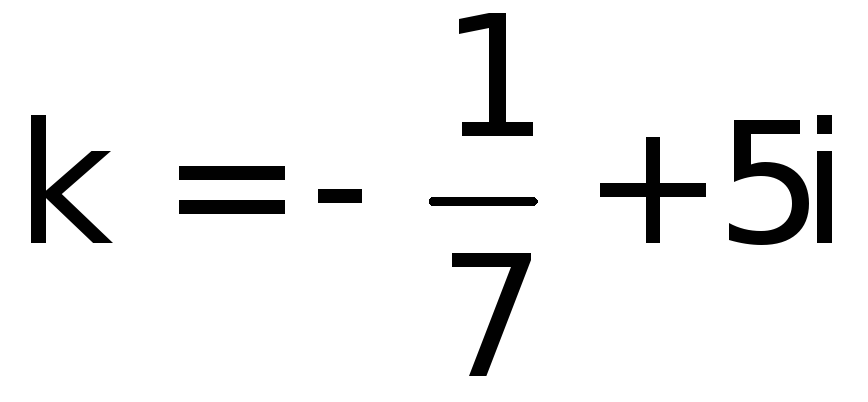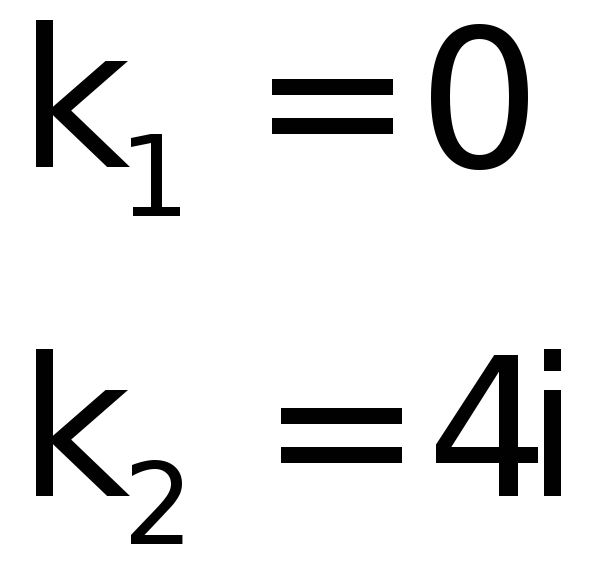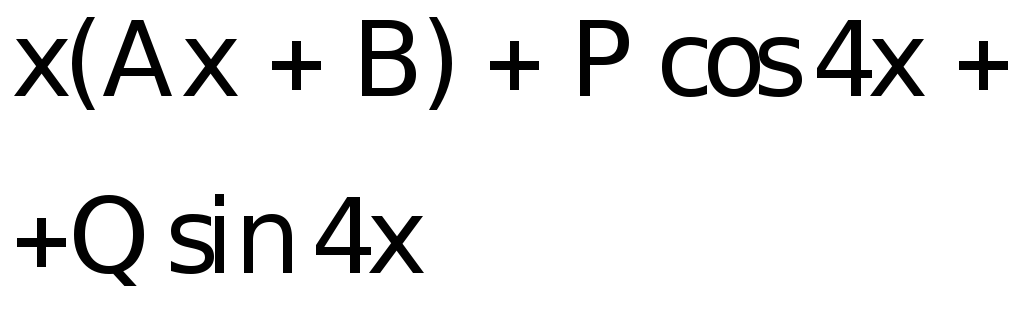- •1) По виду знаменателя находим разложение на простейшие дроби
- •Примеры
- •Примеры
- •2.7. Замена переменной в определенном интеграле
- •Примеры
- •2.8 Несобственные интегралы
- •2.8.1. Интегралы с бесконечными пределами (несобственные интегралы I рода)
- •Примеры
- •2.8.2. Несобственные интегралы от неограниченных функций (несобственные интегралы II рода)
- •Примеры
- •2.9. Вычисление площади плоской фигуры
- •2.9.1. Площадь фигуры, ограниченной графиками непрерывных функций
- •2.9.2. Площадь фигуры, ограниченной кривой, заданной параметрически
- •Вспомогательная таблица для построения параметрически заданной кривой
- •2.9.3. Площадь фигуры, ограниченной кривой, заданной в полярных координатах
- •Вспомогательная таблица для построения кривой, заданной в полярных координатах
- •Функции многих переменных
- •Линии и поверхности уровня
- •1. Решить линейные однородные дифференциальные уравнения.
- •3. Решить линейные неоднородные дифференциальные уравнения.
- •4. Найти решение задачи Коши для системы линейных дифференциальных уравнений.
- •5. Найти общее решение системы линейных дифференциальных уравнений.
1. Решить линейные однородные дифференциальные уравнения.
а)
![]()
б)
![]()
в)
![]()
г)
![]()
д)
![]()
е)
![]()
ж)
![]()
Решение:
а)
Составим характеристическое уравнение
![]()
Т.к.
![]() ,
корни действительны и различны. По
теореме Виета
,
корни действительны и различны. По
теореме Виета
![]()
![]()
Запишем общее
решение:
![]()
б)
Составим характеристическое уравнение
![]()
Т.к.
![]() ,
корни действительны и различны и равны:
,
корни действительны и различны и равны:
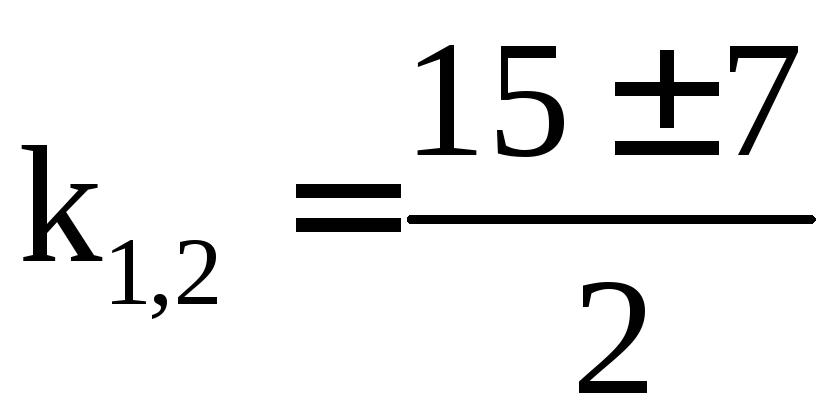 ,
,
![]() ,
,
![]()
Запишем общее
решение:
![]()
в)
Запишем характеристическое уравнение:
![]()
Т.к.
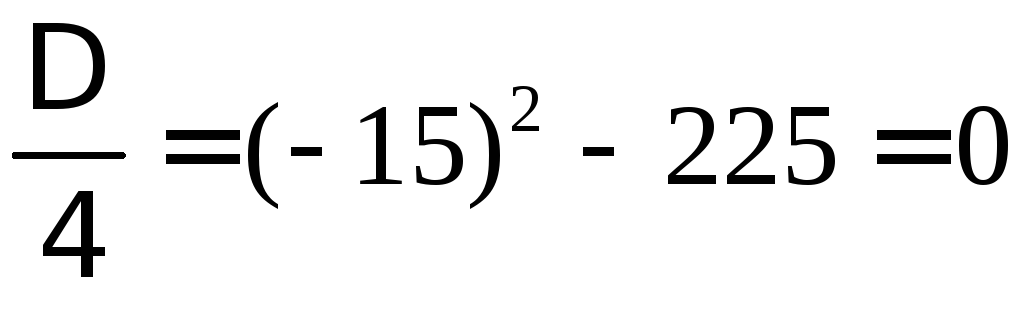 ,
корень
,
корень
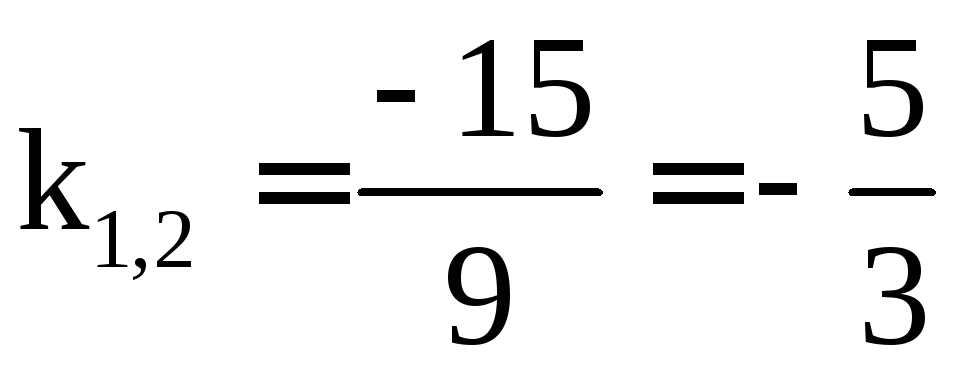 кратный, и общее решение запишется в
виде:
кратный, и общее решение запишется в
виде:
![]()
г)
Запишем характеристическое уравнение:
![]()
Т.к.
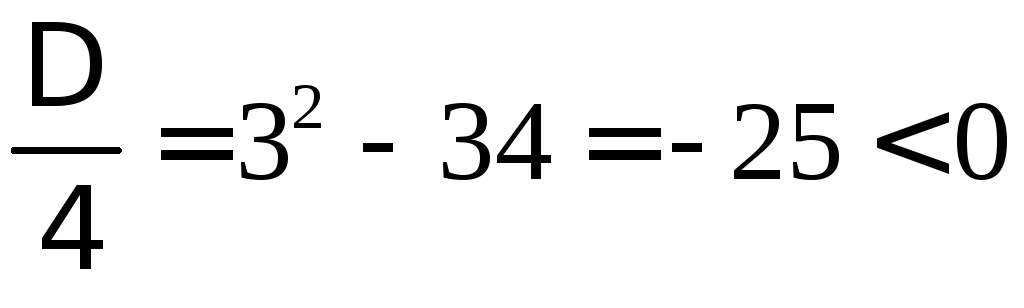 корни комплексно сопряженные и равные
корни комплексно сопряженные и равные
![]() ,
записываем общее решение:
,
записываем общее решение:
![]()
д)
характеристическое уравнение имеет
вид:
![]() или
или
![]() откуда получаем,
что корни характеристического уравнения
откуда получаем,
что корни характеристического уравнения
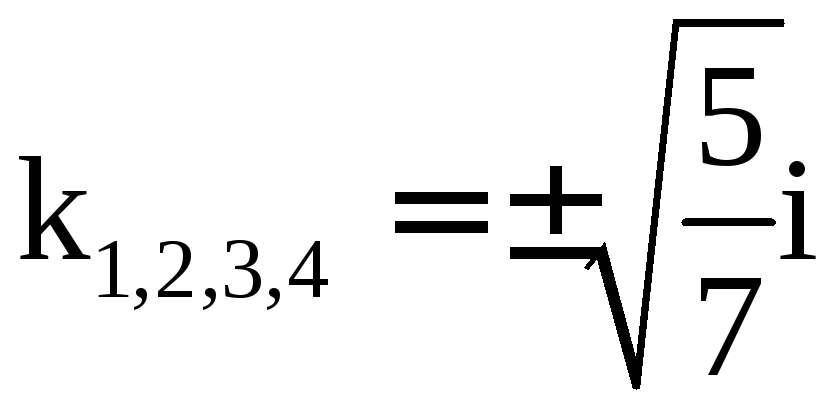 чисто мнимые и имеют кратность 2, откуда
чисто мнимые и имеют кратность 2, откуда
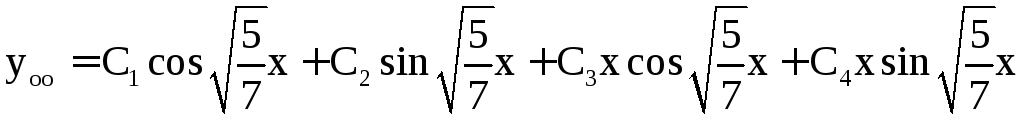
е)
характеристическое уравнение
![]() имеет корни
имеет корни
![]() ,
,
![]() ,
,
![]()
Запишем теперь
общее решение:
![]()
ж)
характеристическое уравнение
![]() имеет один действительный корень
имеет один действительный корень
![]() и два комплексно сопряженных
и два комплексно сопряженных
![]()
Запишем общее
решение:
![]()
2.
Решить задачу Коши:
![]() ;
;
![]() ;
;
![]()
Решение:
Найдем вначале общее решение.
Характеристическое уравнение
![]() имеет корни
имеет корни![]() ,
,
![]() .
Отсюда получаем общее решение:
.
Отсюда получаем общее решение:
![]()
Теперь найдем
![]() и
и![]() .
Для этого найдем
.
Для этого найдем![]() и подставим начальные условия:
и подставим начальные условия:![]() ,
,![]() .
Решим полученную систему
.
Решим полученную систему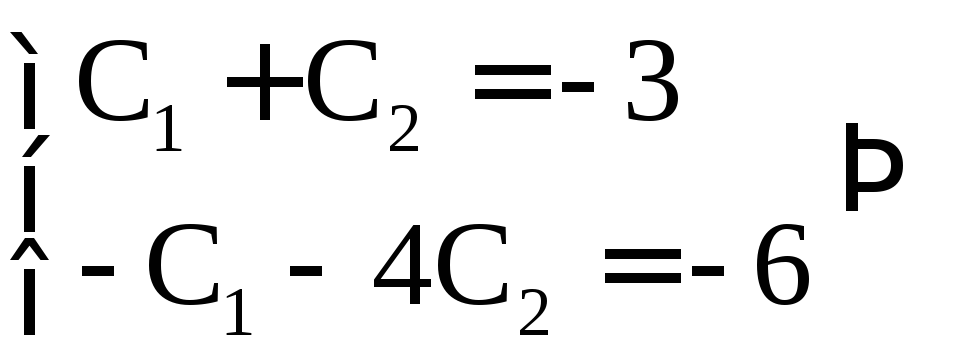

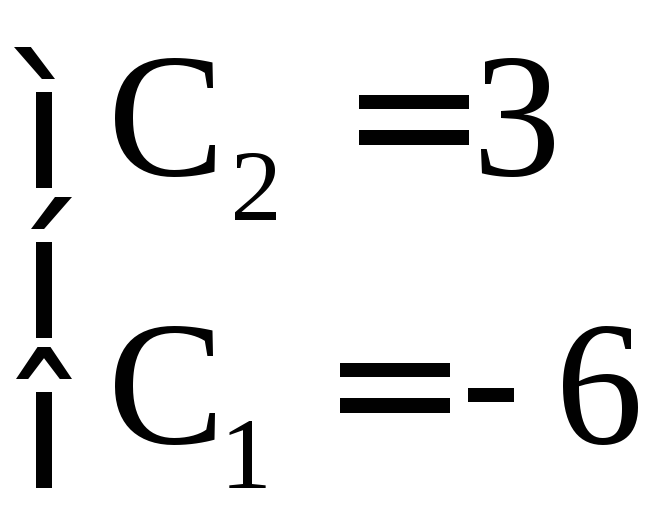
Подставим найденные
значения
![]() и
и![]() в общее решение:
в общее решение:
Итак
![]()
|
Корни характеристического уравнения |
Правая часть |
Контрольное число |
Вид yчн |
|
-2,5 |
|
|
|
|
7; |
|
|
|
|
2;-8 |
|
|
|
|
3;-5 |
|
|
|
|
|
|
|
|
|
0;-2 |
|
|
|
|
-1;0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0;-4 |
|
|
|
3. Решить линейные неоднородные дифференциальные уравнения.
а)
![]()
б)
![]()
в)
![]()
г)
![]()
д)
![]()
е)
![]()
ж)
![]()
Решение:
а) Решим
сначала однородное уравнение; для чего
составим характеристическое уравнение
и найдем его корни:
![]() ,
,![]() ,
,![]() ,
,![]() .
Найдем общее решение:
.
Найдем общее решение:![]() .
Найдем по правой части контрольное
число. Т.к.
.
Найдем по правой части контрольное
число. Т.к.![]() - многочлен второй степени, то его
контрольное число
- многочлен второй степени, то его
контрольное число![]() ,
а поскольку ононе
совпадает с
корнями характеристического уравнения
(нерезонансный случай), значит yчн
будем искать в виде:
,
а поскольку ононе
совпадает с
корнями характеристического уравнения
(нерезонансный случай), значит yчн
будем искать в виде:![]() .
.
Найдем коэффициенты A, B, C.
Коэффициенты
взяты из уравнения

Составим систему для нахождения из уравнения: A, B, C, для чего найдем коэффициенты при степенях x2, x и 1 в левой и правой частях уравнения:
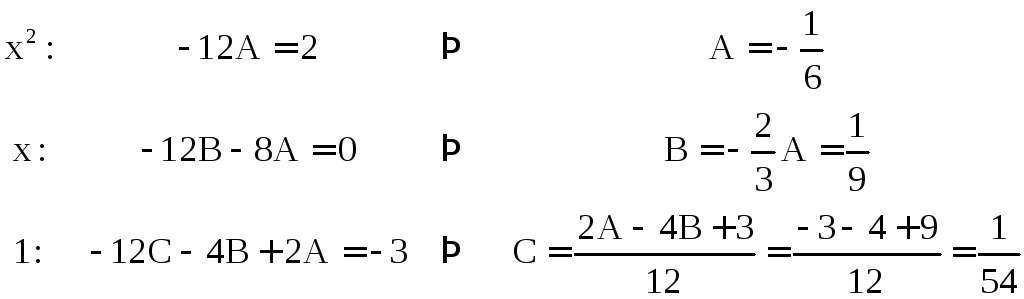
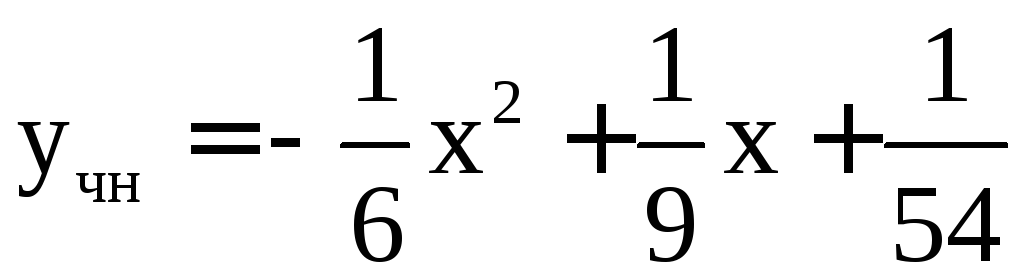
Окончательно
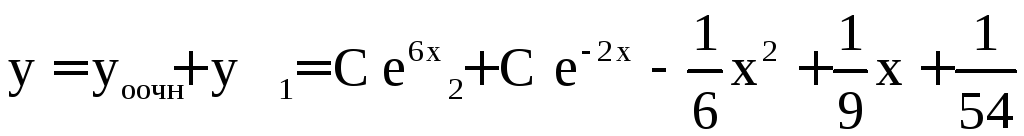
б) Характеристическое
уравнение:
![]() ,
,![]() ,
,![]() .
Запишем
.
Запишем![]() .
.
Найдем по правой
части
![]() .
Контрольное числоk=d=1,
которое не
совпадает
с корнями характеристического уравнения.
Найдем вид
.
Контрольное числоk=d=1,
которое не
совпадает
с корнями характеристического уравнения.
Найдем вид
![]() .
.
Найдем коэффициенты:
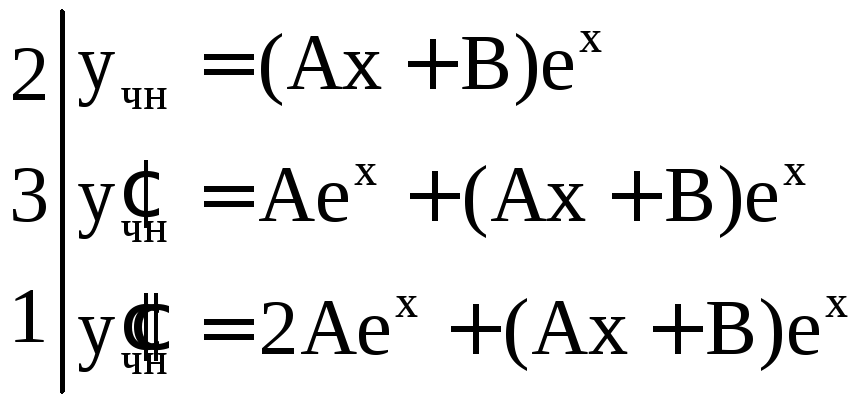
и приравняем коэффициенты в левой и правой частях уравнения:
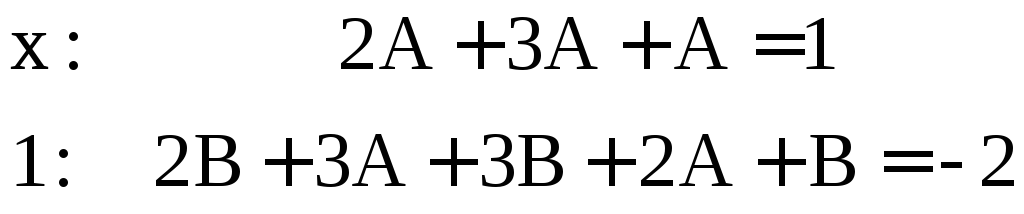
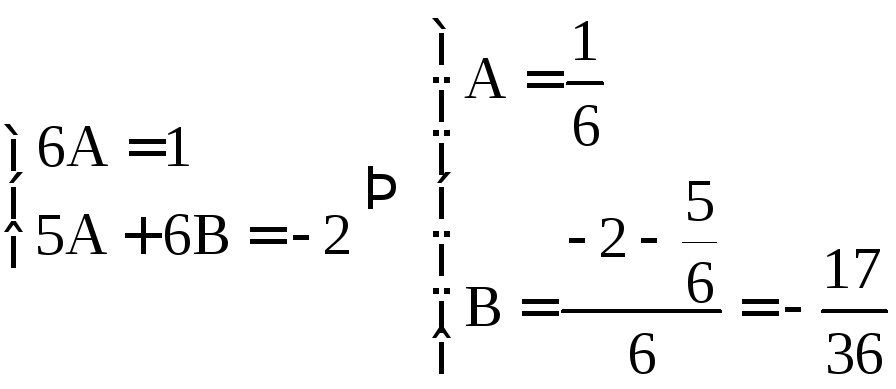
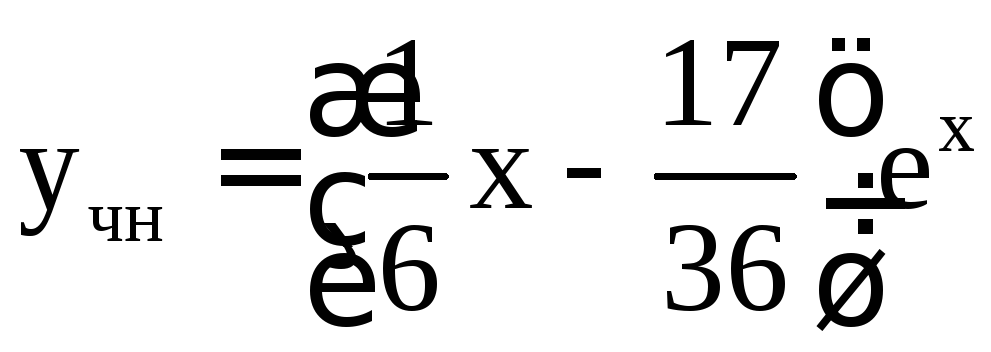 .
По теореме об общем решении
.
По теореме об общем решении
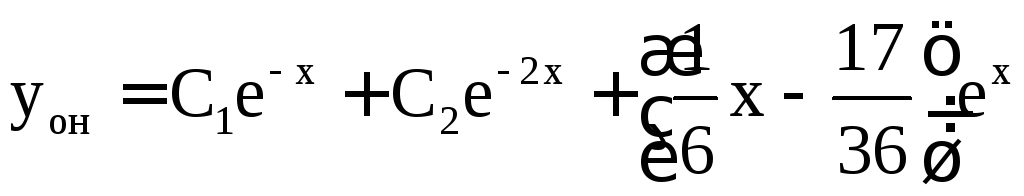 .
.
в) Характеристическое
уравнение:![]() ,
,![]() ,
,![]()
![]() ,
,![]() .
Контрольное число
.
Контрольное число![]() совпадает с
корнем характеристического уравнения:
Найдем вид
совпадает с
корнем характеристического уравнения:
Найдем вид
![]() .
.
Найдем коэффициенты:
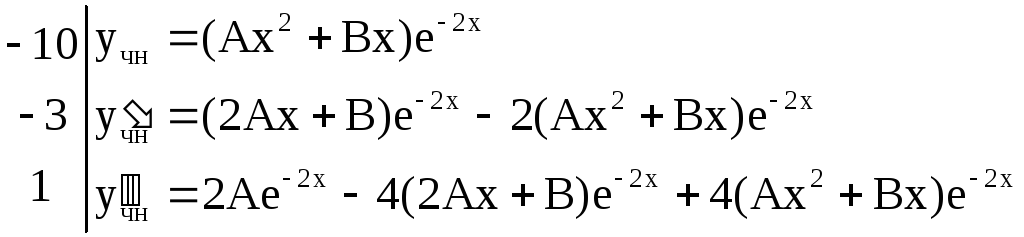

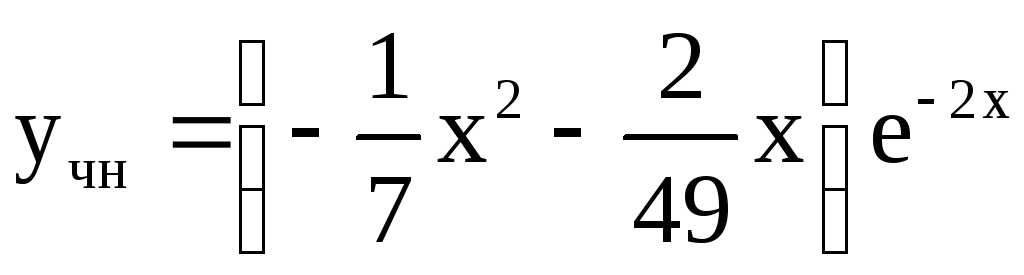 ,
,
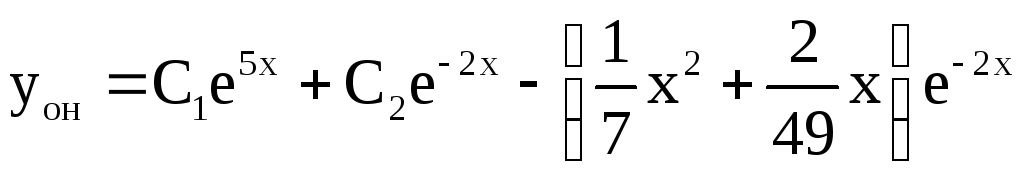
г)
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Поскольку контрольное число
.
Поскольку контрольное число
![]() совпадает с
кратным корнем
характеристического уравнения
совпадает с
кратным корнем
характеристического уравнения
![]()
![]() ищем в виде:
ищем в виде:
![]() .
.
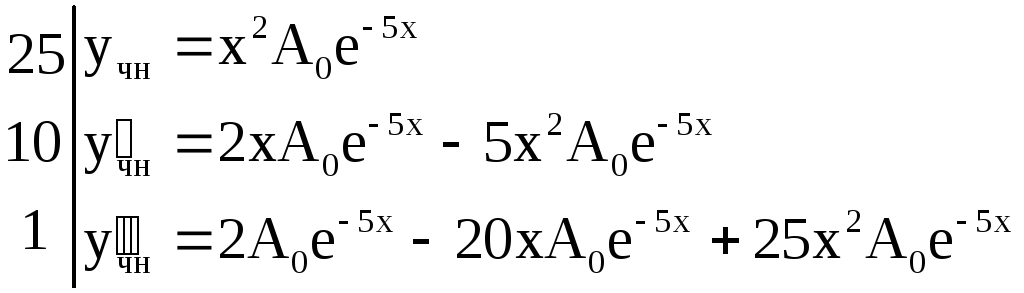
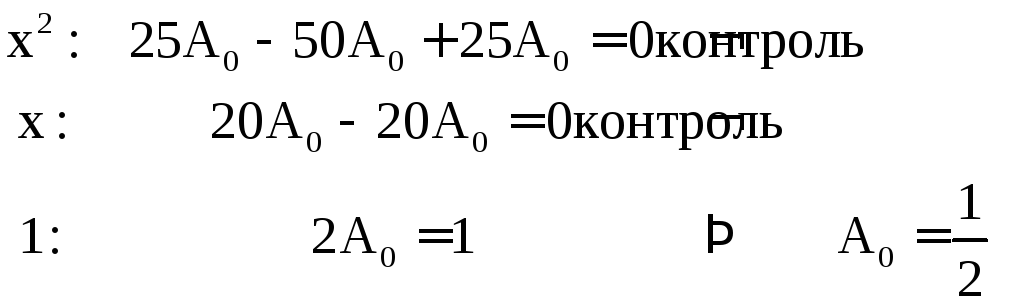
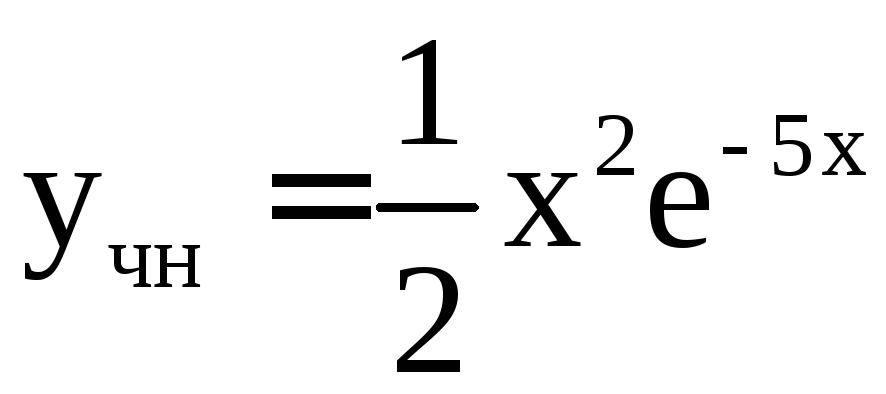 .
Итак
.
Итак
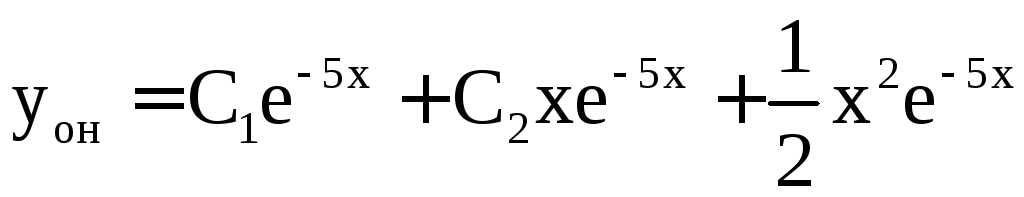
д)
![]()
![]() ,
,
![]() ,
,![]() .
Т.к. контрольное число
.
Т.к. контрольное число![]() не совпадает
с корнями характеристического уравнения
(нерезонансный случай), то решение ищем
в виде
не совпадает
с корнями характеристического уравнения
(нерезонансный случай), то решение ищем
в виде
![]() .
Найдем коэффициентыP
и Q
.
Найдем коэффициентыP
и Q
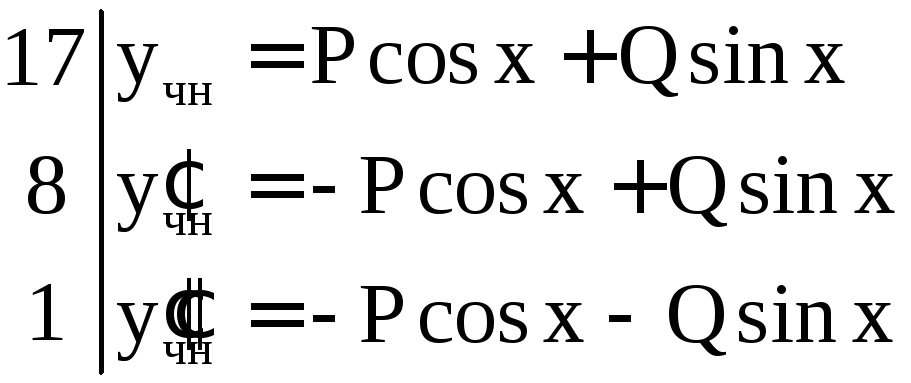 Составим систему:
Составим систему:
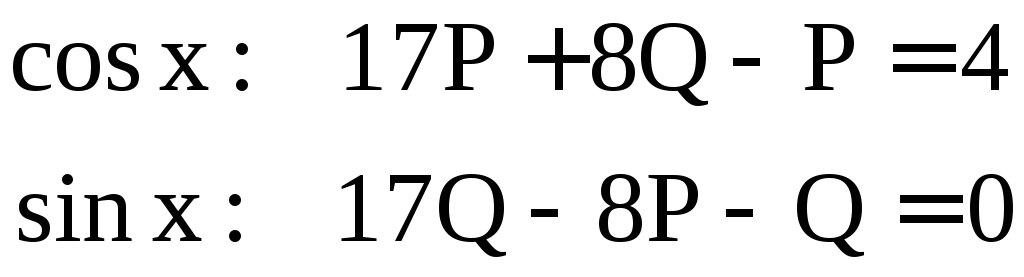
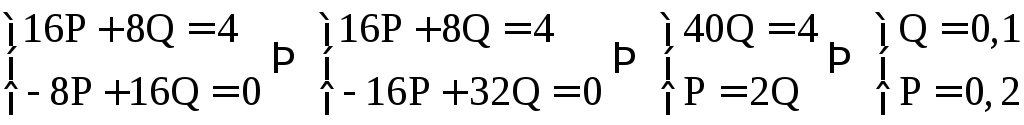
Итак
![]()
Окончательно
![]()
е)
![]()
![]() ,
,
![]() ,
,![]()
Контрольное число
![]() совпадает
с одним из корней характеристического
уравнения (резонансный случай)
совпадает
с одним из корней характеристического
уравнения (резонансный случай)
![]()
![]() ищем в виде:
ищем в виде:
![]()
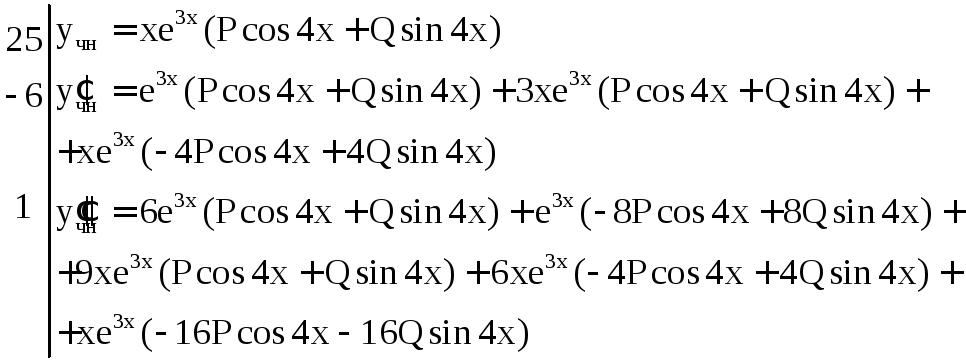
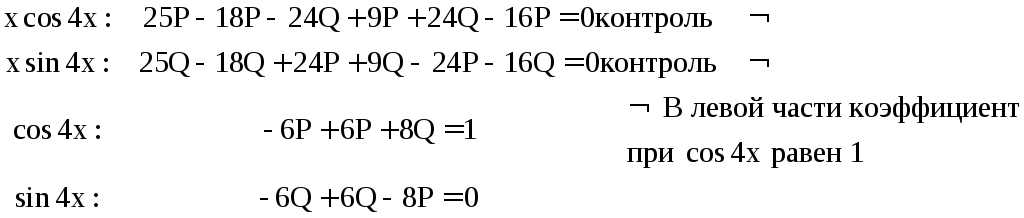
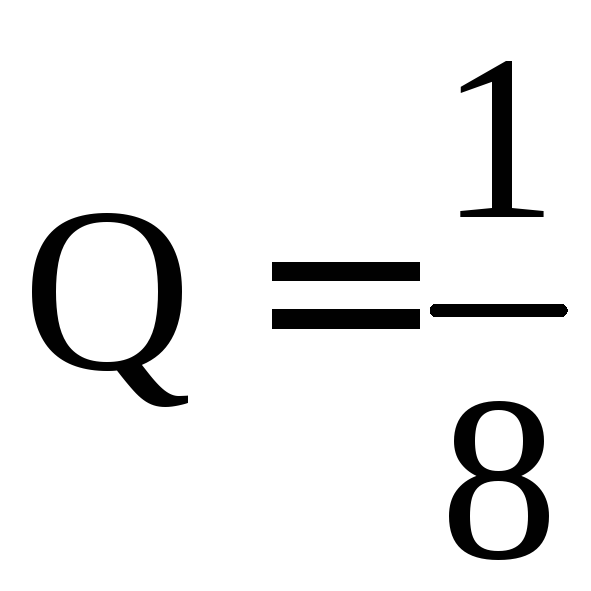 ,
,
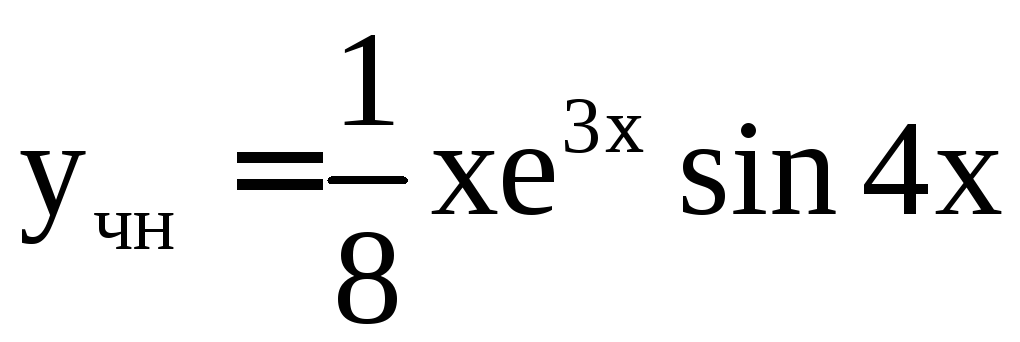
Ответ:
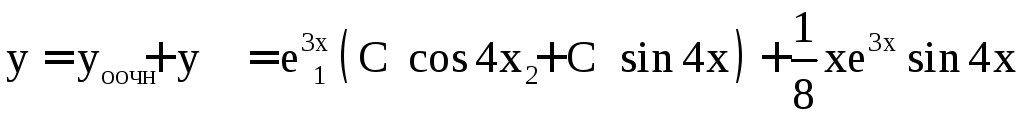
ж)
![]()
Поскольку в правой части стоят функции с различными контрольными числами, то воспользуемся теоремой наложения.
Решим однородное
уравнение:
![]() .
.
![]()
![]()
Для нахождения
![]() для правой части
для правой части
![]() .
Его ищем в виде
.
Его ищем в виде![]() ,
т.к. контрольное число
,
т.к. контрольное число![]() не совпадает
с корнем характеристического уравнения.
не совпадает
с корнем характеристического уравнения.
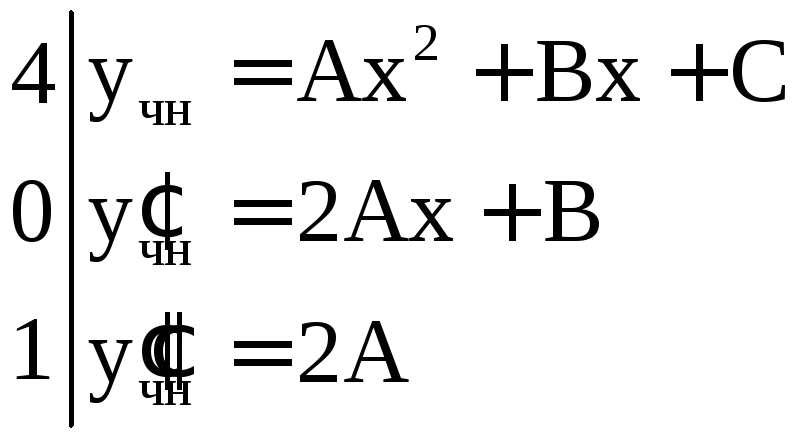
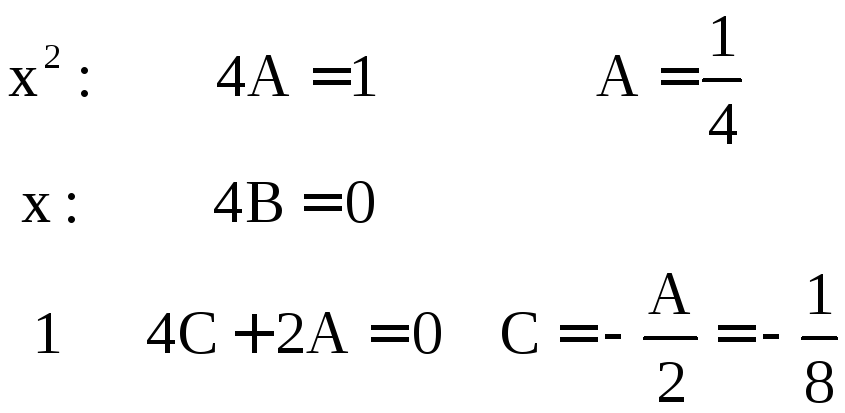
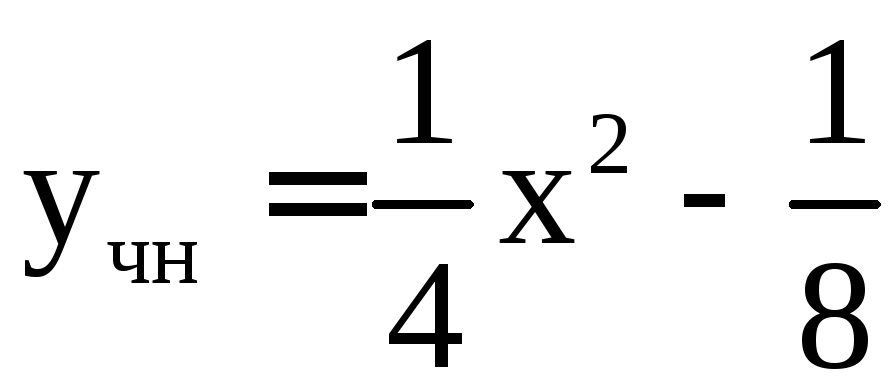
Теперь найдем
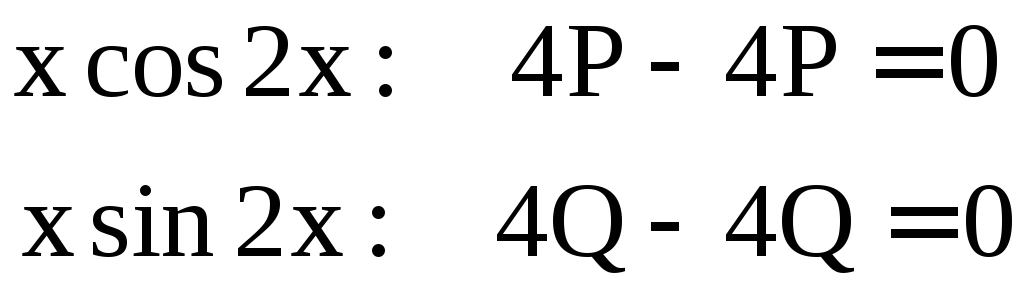
![]() для правой части
для правой части
![]() .
.
Контрольное число
![]() совпадает
с корнем характеристического уравнения
(резонансный случай), поэтому
совпадает
с корнем характеристического уравнения
(резонансный случай), поэтому
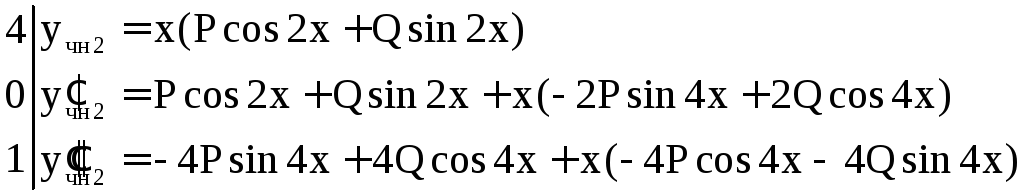
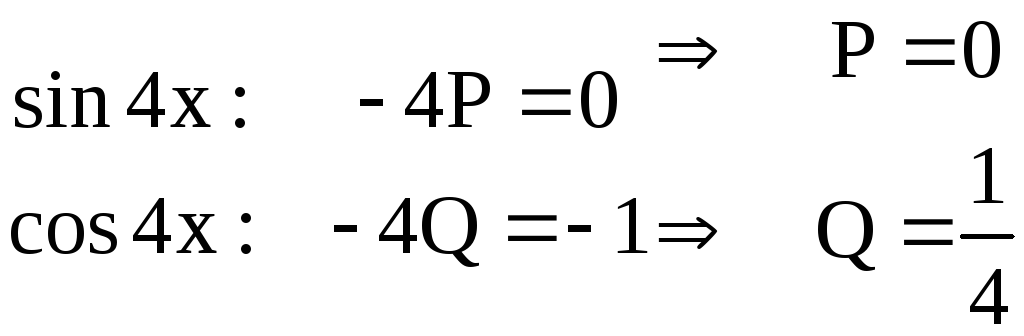

Ответ:
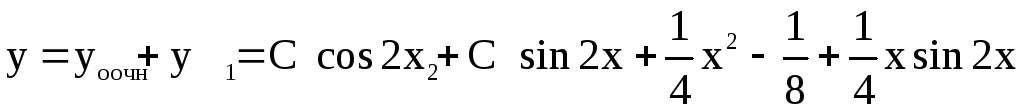 .
.