
- •1) По виду знаменателя находим разложение на простейшие дроби
- •Примеры
- •Примеры
- •2.7. Замена переменной в определенном интеграле
- •Примеры
- •2.8 Несобственные интегралы
- •2.8.1. Интегралы с бесконечными пределами (несобственные интегралы I рода)
- •Примеры
- •2.8.2. Несобственные интегралы от неограниченных функций (несобственные интегралы II рода)
- •Примеры
- •2.9. Вычисление площади плоской фигуры
- •2.9.1. Площадь фигуры, ограниченной графиками непрерывных функций
- •2.9.2. Площадь фигуры, ограниченной кривой, заданной параметрически
- •Вспомогательная таблица для построения параметрически заданной кривой
- •2.9.3. Площадь фигуры, ограниченной кривой, заданной в полярных координатах
- •Вспомогательная таблица для построения кривой, заданной в полярных координатах
- •Функции многих переменных
- •Линии и поверхности уровня
- •1. Решить линейные однородные дифференциальные уравнения.
- •3. Решить линейные неоднородные дифференциальные уравнения.
- •4. Найти решение задачи Коши для системы линейных дифференциальных уравнений.
- •5. Найти общее решение системы линейных дифференциальных уравнений.
Примеры
Вычислить несобственный интеграл или доказать его расходимость.
1)
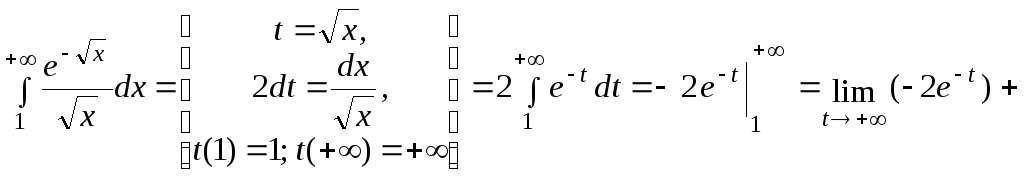
![]() ;
т.к.
;
т.к.
![]() ,
т.е. интеграл сходится.
,
т.е. интеграл сходится.
2)
![]() .
Поскольку
.
Поскольку![]() ,
подынтегральная функция непрерывна в
области интегрирования. Сделаем замену
,
подынтегральная функция непрерывна в
области интегрирования. Сделаем замену![]() (см. п. 1.6), получим:
(см. п. 1.6), получим: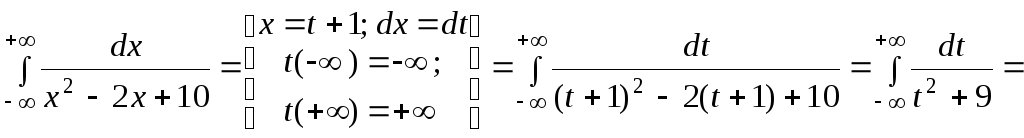
![]() ,
поскольку
,
поскольку![]() нечетная функция, а
нечетная функция, а![]() .
.
3)
![]() .
Подынтегральная функция непрерывна в
области интегрирования. Удобна замена
.
Подынтегральная функция непрерывна в
области интегрирования. Удобна замена![]() ,
являющаяся непрерывной и монотонной в
области интегрирования:
,
являющаяся непрерывной и монотонной в
области интегрирования:![]()
![]() ,
поскольку
,
поскольку
![]() ,
интеграл расходится.
,
интеграл расходится.
2.8.2. Несобственные интегралы от неограниченных функций (несобственные интегралы II рода)
Если функция
![]() непрерывна
при
непрерывна
при
![]() и
и![]() ,
то по определению
,
то по определению![]() .
(36)
.
(36)
Если функция
![]() непрерывна
при
непрерывна
при
![]() и
и![]() ,
то
,
то![]() .
(37)
.
(37)
Если функция имеет
бесконечный разрыв во внутренней точке
![]() промежутка
промежутка![]() ,
то по определению полагают:
,
то по определению полагают:![]() (38)
(38)
Порядок вычисления несобственного интеграла от неограниченных функций аналогичен порядку вычисления несобственного интеграла с бесконечными пределами. Определения сходящегося и расходящегося интегралов аналогичны соответствующим для несобственных интегралов с бесконечными пределами. Интеграл (38) сходится, если существуют и конечны оба предела.
Как и в п. 2.8.1. можно записать аналог формулы Ньютона-Лейбница:
![]() ,
(39)
,
(39)
если
![]() непрерывна на
непрерывна на![]() ,
а под
,
а под![]() понимается
понимается![]() .
.
Аналогично
![]() ,
(40)
если
,
(40)
если
![]() непрерывна на
непрерывна на![]() ,
а
,
а![]() .
.
![]()
![]() ,
где
,
где
![]() - точка бесконечного разрыва подынтегральной
функции,
- точка бесконечного разрыва подынтегральной
функции,![]() первообразные функции
первообразные функции![]() на участках
на участках![]() и
и![]() ,
на которых
,
на которых![]() непрерывна. Интеграл в последнем случаесходится,
если существуют и конечны оба
предела
непрерывна. Интеграл в последнем случаесходится,
если существуют и конечны оба
предела
![]() и
и![]() .
Если хотя бы один из пределов не существует
или бесконечен, то интегралрасходится.
.
Если хотя бы один из пределов не существует
или бесконечен, то интегралрасходится.
Интегрирование по частям и способ подстановки см. в п. 2.8.1.
Примеры
Вычислить несобственный интеграл или доказать его расходимость.
![]() .
Подынтегральная функция терпит разрыв
в точке
.
Подынтегральная функция терпит разрыв
в точке
![]() ,
поэтому
,
поэтому ,
поскольку
,
поскольку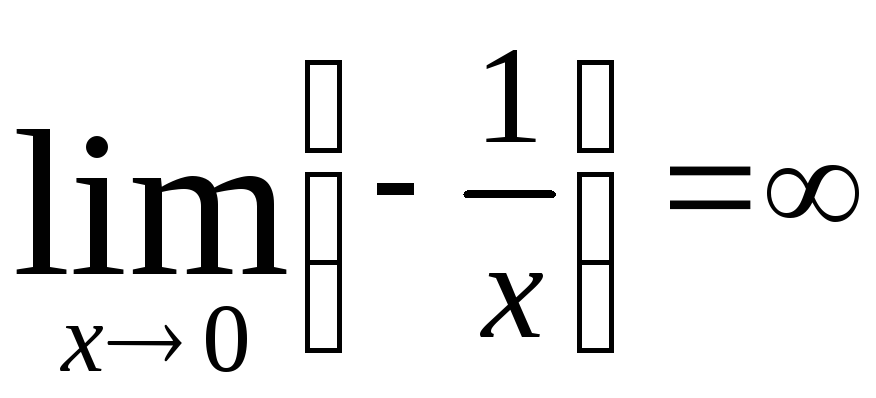 ,
интеграл расходится.
,
интеграл расходится.
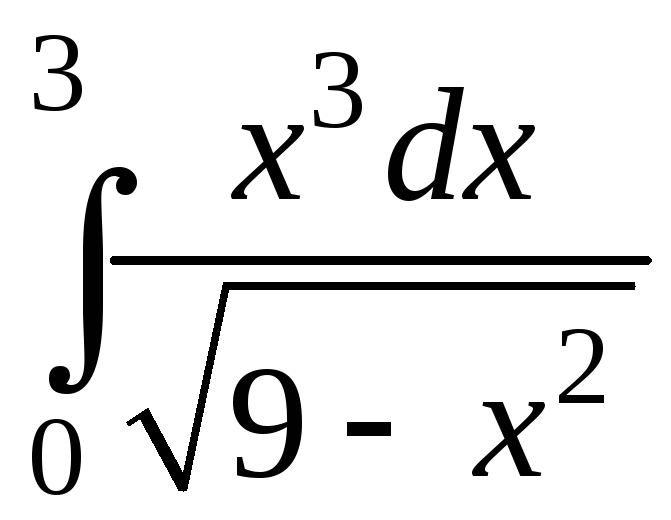 .
Подынтегральная функция обращается в
бесконечность в точке
.
Подынтегральная функция обращается в
бесконечность в точке
![]() .
Сделаем замену
.
Сделаем замену![]() ,
монотонную в области интегрирования
,
монотонную в области интегрирования![]() :
:
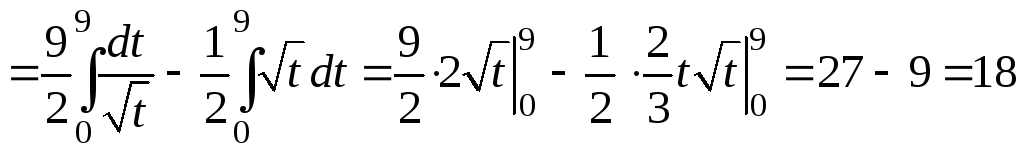 ,
т.е. интеграл сходится.
,
т.е. интеграл сходится.
3)
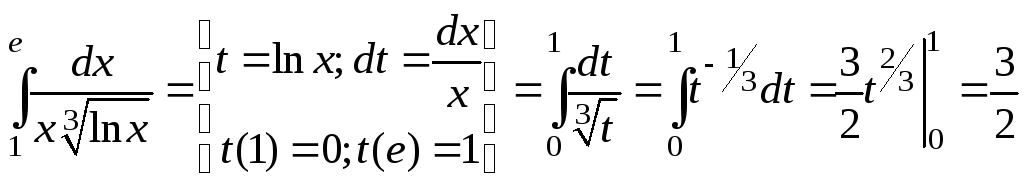 ;
интеграл сходится.
;
интеграл сходится.
4)
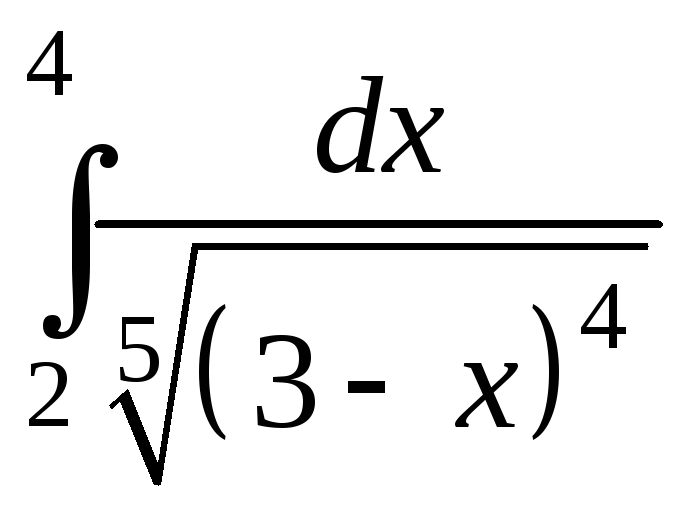 .
Подынтегральная функция непрерывна в
области интегрирования всюду, кроме
точки
.
Подынтегральная функция непрерывна в
области интегрирования всюду, кроме
точки![]() .
В качестве первообразной на обоих
промежутках
.
В качестве первообразной на обоих
промежутках![]() и
и![]() можно взять функцию
можно взять функцию![]() ,
поэтому
,
поэтому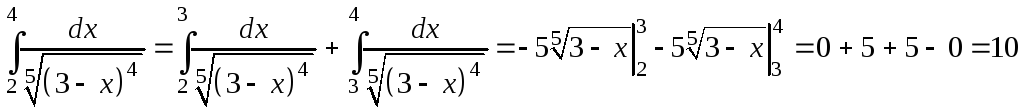 т.е.
интеграл сходится.
т.е.
интеграл сходится.
2.9. Вычисление площади плоской фигуры
Задача вычисления площади плоской фигуры, которая привела нас к понятию определенного интеграла, была рассмотрена в п. 1.1. В данном подразделе рассмотрим задачу вычисления площади плоской фигуры в более общей ситуации и для различных способов задания кривой.
2.9.1. Площадь фигуры, ограниченной графиками непрерывных функций
Пусть
![]() и
и![]() - две непрерывные функции и
- две непрерывные функции и![]() - две прямые (рис. 3). Площадь фигуры,
ограниченной данными линиями вычисляется
по формуле:
- две прямые (рис. 3). Площадь фигуры,
ограниченной данными линиями вычисляется
по формуле:
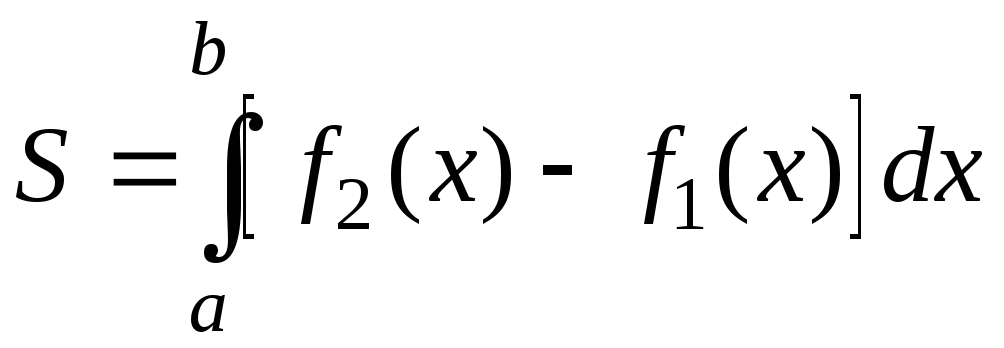 .
(41)
.
(41)
Порядок вычисления:
построить чертеж;
найти пределы интегрирования;
применить формулу (41).
Пример. Найти
площадь плоской фигуры, ограниченной
параболой и прямой:
![]() .
.
Решение. Построим
чертеж данной фигуры (рис. 4). Найдем
пределы интегрирования, решив систему
уравнений:
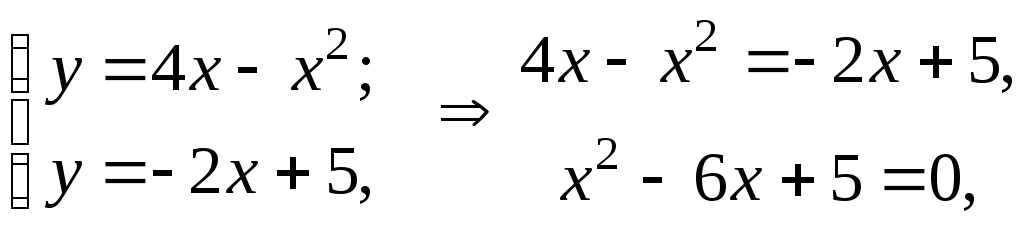 отсюда
отсюда![]() ,
значит, пределы интегрирования
,
значит, пределы интегрирования![]() .
Применяем формулу
.
Применяем формулу
![]() (кв. ед.).
(кв. ед.).
