
- •1) По виду знаменателя находим разложение на простейшие дроби
- •Примеры
- •Примеры
- •2.7. Замена переменной в определенном интеграле
- •Примеры
- •2.8 Несобственные интегралы
- •2.8.1. Интегралы с бесконечными пределами (несобственные интегралы I рода)
- •Примеры
- •2.8.2. Несобственные интегралы от неограниченных функций (несобственные интегралы II рода)
- •Примеры
- •2.9. Вычисление площади плоской фигуры
- •2.9.1. Площадь фигуры, ограниченной графиками непрерывных функций
- •2.9.2. Площадь фигуры, ограниченной кривой, заданной параметрически
- •Вспомогательная таблица для построения параметрически заданной кривой
- •2.9.3. Площадь фигуры, ограниченной кривой, заданной в полярных координатах
- •Вспомогательная таблица для построения кривой, заданной в полярных координатах
- •Функции многих переменных
- •Линии и поверхности уровня
- •1. Решить линейные однородные дифференциальные уравнения.
- •3. Решить линейные неоднородные дифференциальные уравнения.
- •4. Найти решение задачи Коши для системы линейных дифференциальных уравнений.
- •5. Найти общее решение системы линейных дифференциальных уравнений.
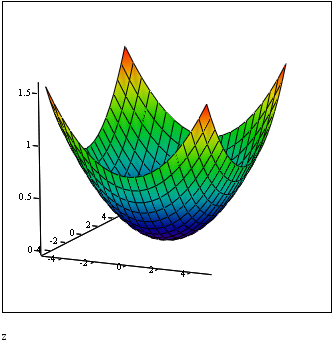
Функции многих переменных
Для упрощения изложения материала и уменьшения объема лекций в теории и примерах данного раздела рассматриваются функции двух переменных. Кроме того, функции двух переменных имеют наглядные геометрические образы в виде трехмерных поверхностей
Пусть дано множество
![]()
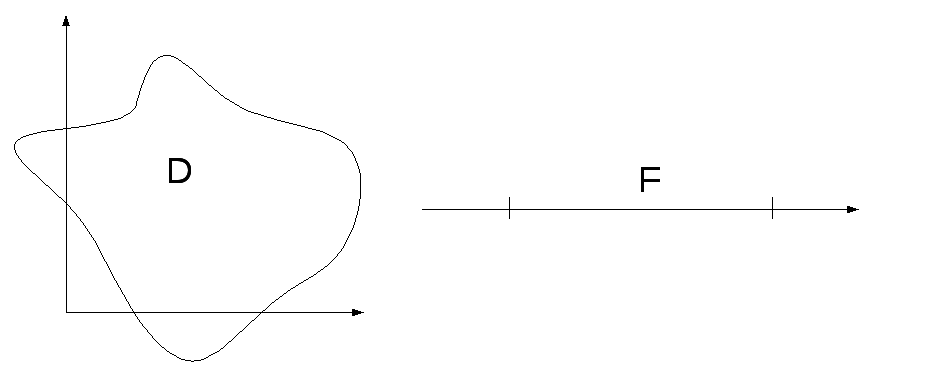
Если указано правило F, по которому каждой точке (x;y) области D поставлено в соответствие число z из множества F, то говорят, что задана функция F(x;y) с областью определения D и множеством значений F.
При этом x,y- независимые переменные (аргументы), z- значение функции в(.) с координатами x,y.
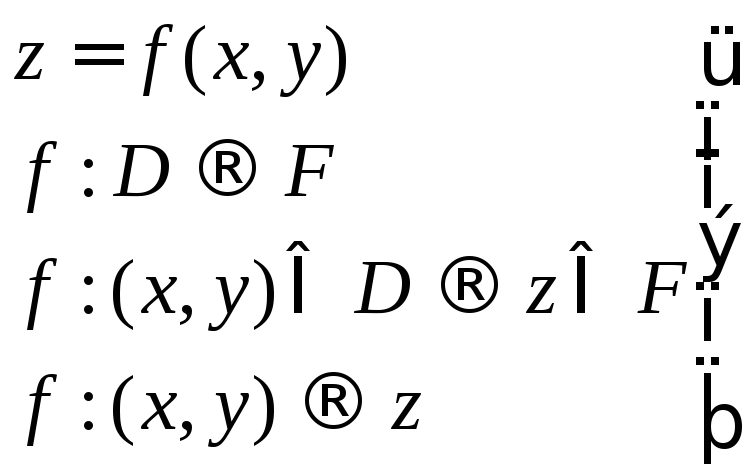 Формы
записи ФНП
Формы
записи ФНП
![]()
Функция 2-х переменных есть функция точки плоскости.
![]()
Область определения функции - множество точек на плоскости
Способы задания функции.
1) Табличный способ
|
Y X |
Y1 |
Y2 |
Y3 |
Y4 |
… |
Yn |
|
X1 |
Z11 |
Z12 |
Z13 |
Z14 |
… |
Y1n |
|
X2 |
Z21 |
Z22 |
Z23 |
Z24 |
… |
Y2n |
|
X3 |
Z31 |
Z32 |
Z33 |
Z34 |
… |
Y3n |
|
X4 |
Z41 |
Z42 |
Z43 |
Z44 |
… |
Y4n |
|
… |
… |
… |
… |
… |
… |
… |
|
Xm |
Zm1 |
Zm2 |
Zm3 |
Zm4 |
… |
Ymn |
2) Аналитический. В виде формулы.
(1)
![]()
Область определения
функции:
![]()
Множество значений
функций:
![]()
 (2)
(2)
![]()
Область определения
функции:
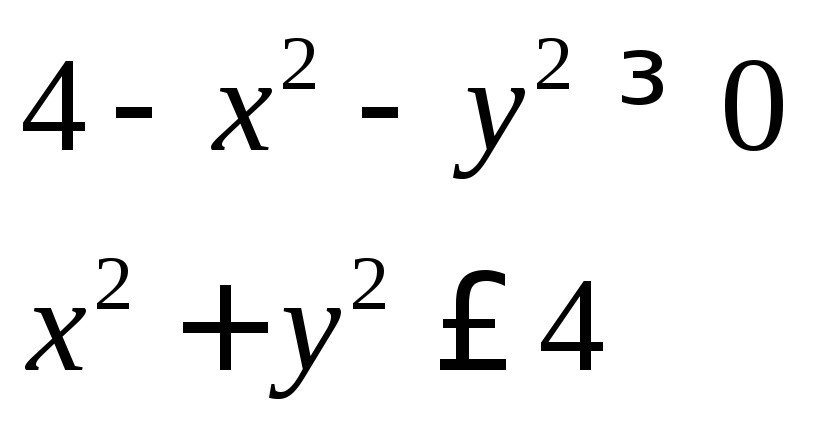
Множество значений
функций:![]()
(3)
![]()
Область определения
функции:
![]() (плоскость)
(плоскость)
Множество значений
функций:![]() (все действительные числа)
(все действительные числа)
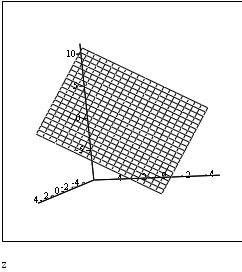
3) Графический способ
Графиком функции
![]() называют геометрическое место точек
называют геометрическое место точек![]() (т.е
поверхность в трёхмерном пространстве).
(т.е
поверхность в трёхмерном пространстве).
Предел функции 2-х переменных
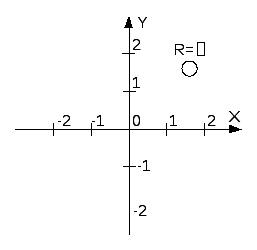
Множество всех
точек М с координатами (x;y)
таких, что
![]() называют
называют![]() -
окрестностью с координатами центра
-
окрестностью с координатами центра![]()
Рассмотрим
последовательность
![]() .
.
Последовательность
![]() называется сходящейся к точке
называется сходящейся к точке![]() ,
что
,
что![]()
![]()
![]()
![]()
![]()
Иными словами,
если найдется такое число N,
что все точки c
номером, большим N,
будут ближе, чем на некотором наперед
заданном сколь угодно малом расстоянии
от точки N,
то такая последовательность точек
![]() называется сходящейся к точке
называется сходящейся к точке![]() .
.
Определение предела
1) Пусть функция
![]() определена на
определена на![]() и пусть точка М или принадлежит, или не
принадлежит ей, но в любой
и пусть точка М или принадлежит, или не
принадлежит ей, но в любой![]() окружности
окружности![]() содержится хотя бы одна (.) множества
М отличная от
содержится хотя бы одна (.) множества
М отличная от![]() .
Если это выполняется, то
.
Если это выполняется, то![]() (по другому,
(по другому,![]() )
)
2) Число А называется
пределом функции
![]() в
точке
в
точке![]()
![]()
![]()
![]()
![]()
![]()
Свойства пределов:
1
![]()
2![]()
Пример:
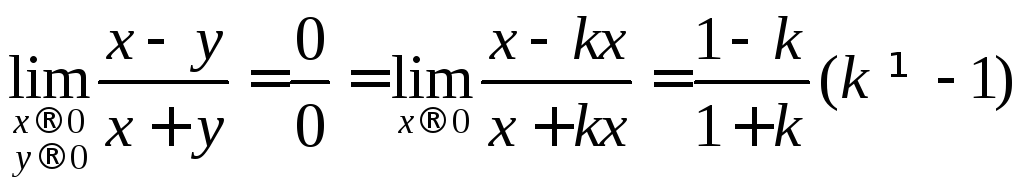
Пусть
![]() т.к зависит от
т.к зависит от![]()
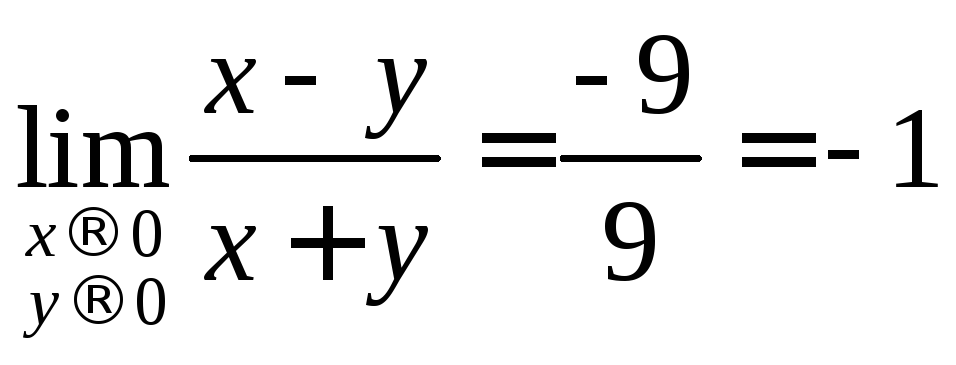
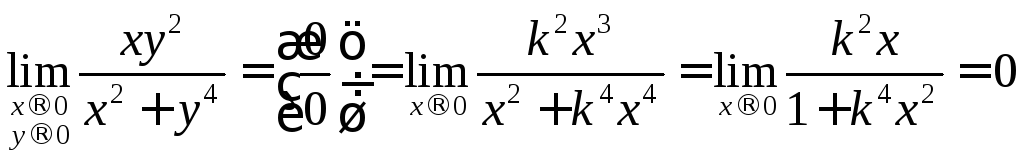
Пусть
![]()
![]() данного предела
данного предела
Функция
![]() называется бесконечно малой в точке
называется бесконечно малой в точке![]() если
если![]()
Функция
![]() называется бесконечно большой в точке
называется бесконечно большой в точке![]() если
если![]()
Непрерывность функции 2-х переменных.
![]() называется
непрерывной в точке
называется
непрерывной в точке![]() ,
если
,
если![]() .
.
Точки в которых функция не обладает свойством непрерывности, называются точками разрыва.
Полным приращением
функции
![]() называется функция
называется функция![]()
Функция
![]() называется непрерывной в точке
называется непрерывной в точке![]() ,
если её полное приращение
,
если её полное приращение![]() при
при![]() .
.
![]()
Функция называется непрерывной на некотором множестве, если она непрерывна в каждой (.) этого множества
Линии и поверхности уровня
Линией
уровня
функции
![]() называется линия
называется линия![]() на плоскости
на плоскости![]() в (.) которой функция
в (.) которой функция![]() принимает одно и то же значение.
принимает одно и то же значение.
Поверхностью
уровня
функции
![]() называется поверхность
называется поверхность![]() ,
в точках которой функция имеет постоянное
значение С.
,
в точках которой функция имеет постоянное
значение С.
Пример нахождения линий и поверхностей уровня:
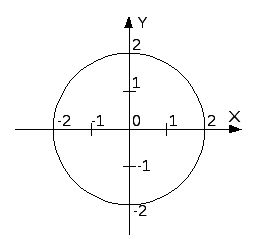
1. Найти линию
уровня для функции
![]() .
.
![]()
![]()
Преобразуем данное выражение к каноническому виду:
![]()
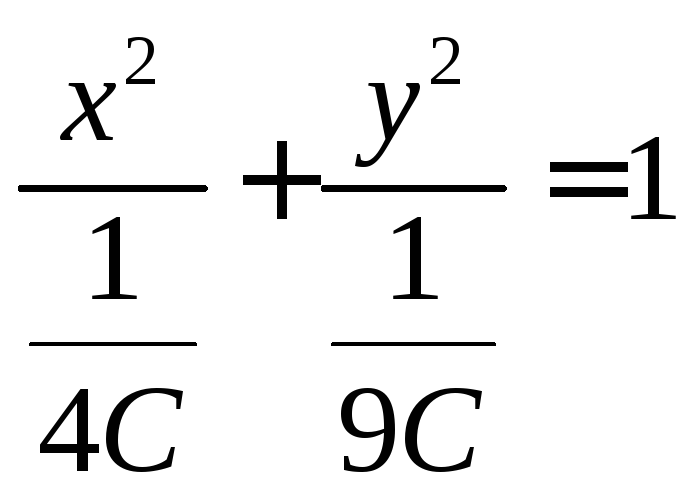
Получили уравнение семейства эллипсов с полуосями
![]()
![]()
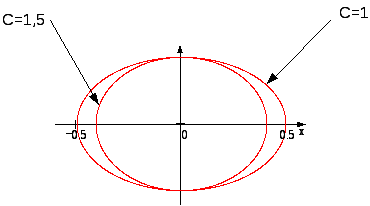
На рисунке построены линии уровня заданной функции для двух значений параметра С.
2. Построить поверхности уровня для функции:
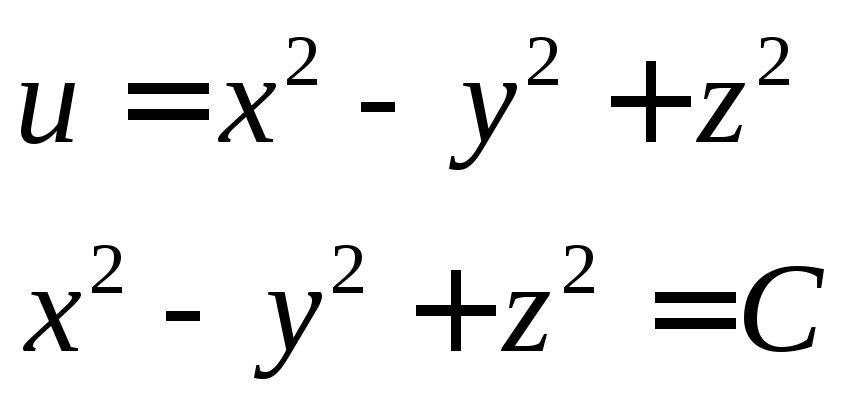
Здесь возможно несколько вариантов:
![]() ,
уравнение поверхности уровня:
,
уравнение поверхности уровня:![]() - конус
- конус
![]() ,
уравнение поверхности уровня:
,
уравнение поверхности уровня:
![]() - семейство однополостных гиперболоидов
- семейство однополостных гиперболоидов
![]() ,
уравнение поверхности уровня:
,
уравнение поверхности уровня:
![]() - семейство двуполостных гиперболоидов
- семейство двуполостных гиперболоидов
Частные производные функции нескольких переменных
Пусть функция
![]() определена в некоторой окрестности
точкиM.
Придадим приращение
определена в некоторой окрестности
точкиM.
Придадим приращение
![]() аргументуx,
оставляя
аргументуx,
оставляя
![]() .
.![]() ,
точка
,
точка![]() .
.
Приращение ФНП
![]() .
.
![]() .
.
Частной производной
функции
![]() по переменнойx
называется выражение
по переменнойx
называется выражение
![]() .
Аналогично, частной производной функции
.
Аналогично, частной производной функции![]() по переменнойy
называется выражение
по переменнойy
называется выражение
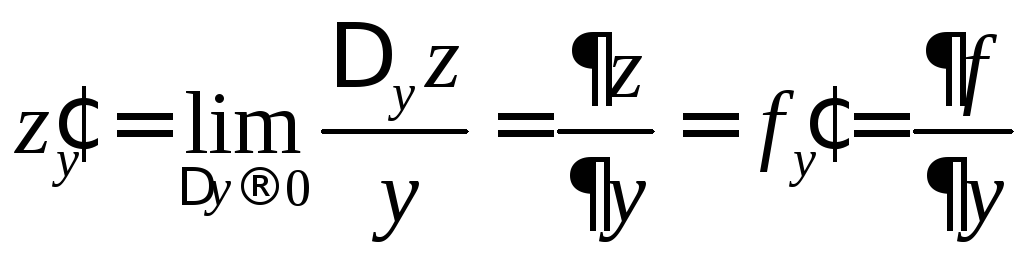 .
.
Пример.
№1.
Дана функция ![]() .Найдем ее частные
производные, учитывая, что при
дифференцировании по одной из переменных
все другие переменные считаются
постоянными.
.Найдем ее частные
производные, учитывая, что при
дифференцировании по одной из переменных
все другие переменные считаются
постоянными.
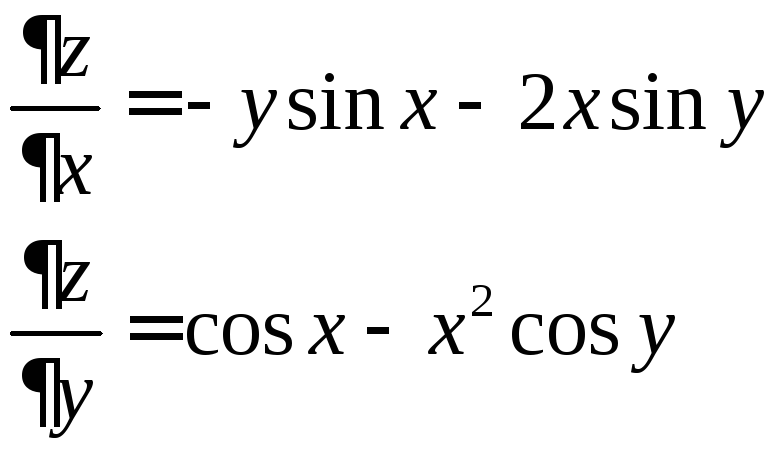
№2
Дана функция
![]() .
Ее частные производные:
.
Ее частные производные:
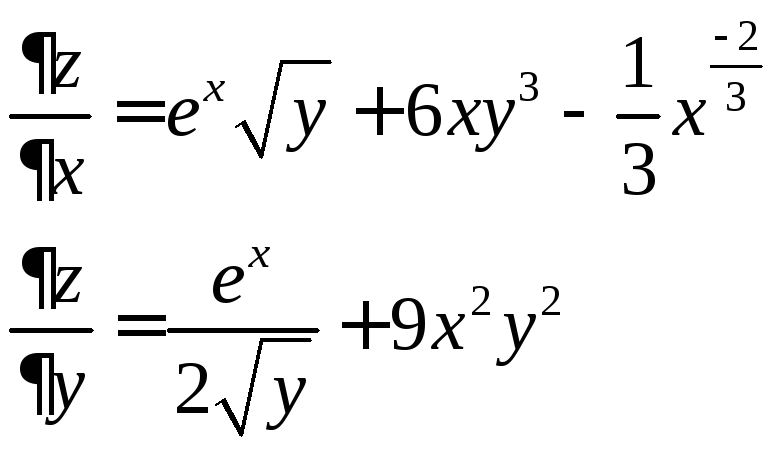
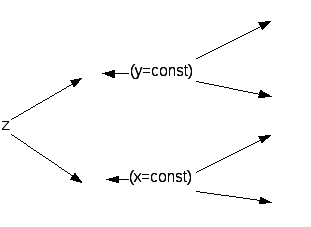
Полный дифференциал функции нескольких переменных. Применение дифференциала в приближенных вычислениях, нормаль и касательная к поверхности, производная сложной функции. Производные и дифференциалы высших порядков, производная неявной функции.
1. Дифференцирование ФНП
Пусть имеется ФНП
![]() .
.
Геометрический смысл:
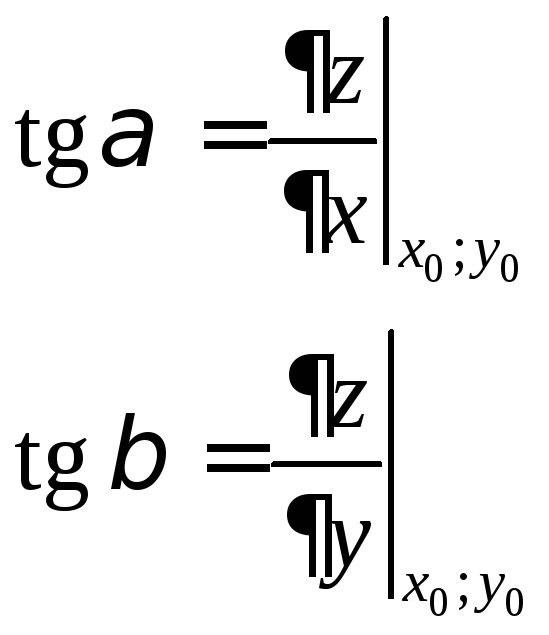
2. Дифференциал ФНП и связь его с существованием частных производных
Дифференциалом функции нескольких переменных будем называть выражение вида:
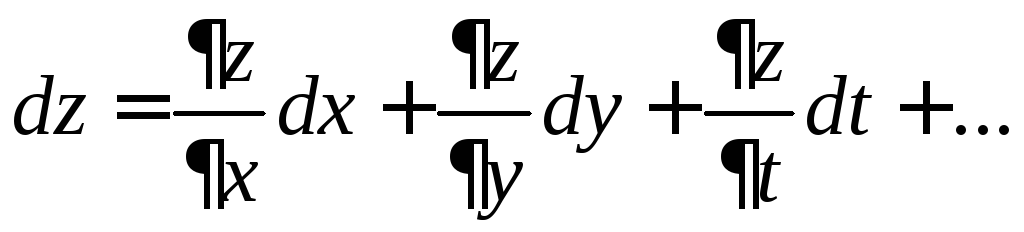
В точке
![]() (принадлежащей области определения
функции):
(принадлежащей области определения
функции):
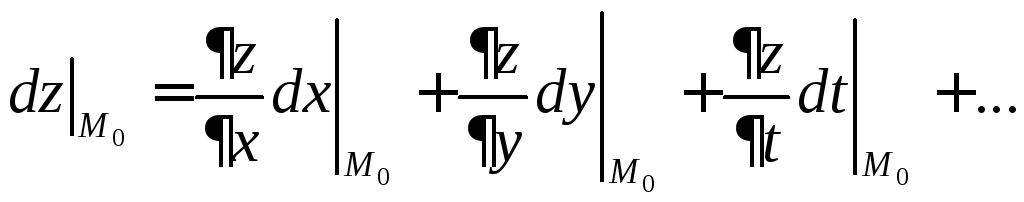
Функция нескольких
переменных
![]() называется дифференцируемой в точке
называется дифференцируемой в точке![]()
![]() ,
если в окрестности этой точки приращение
функции
,
если в окрестности этой точки приращение
функции![]() как
как![]() (1). Причем
(1). Причем![]() ,
то есть
,
то есть![]() является бесконечно
малой более высокого порядка малости
по отношению к бесконечно малой величине
является бесконечно
малой более высокого порядка малости
по отношению к бесконечно малой величине
![]() .
Из существования частных производных
дифференцируемость ФНП, вообще говоря,
не следует.
.
Из существования частных производных
дифференцируемость ФНП, вообще говоря,
не следует.
Из формулы (1) следует формула приближенных вычисления значений дифференцируемой функции с помощью 1-го дифференциала:
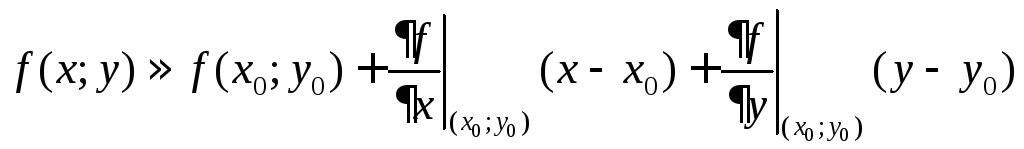 (2)
(2)
Производная сложной функции
Пусть имеется
функция
![]() ,
причем функцииu
и v
сами являются ФНП:
,
причем функцииu
и v
сами являются ФНП:
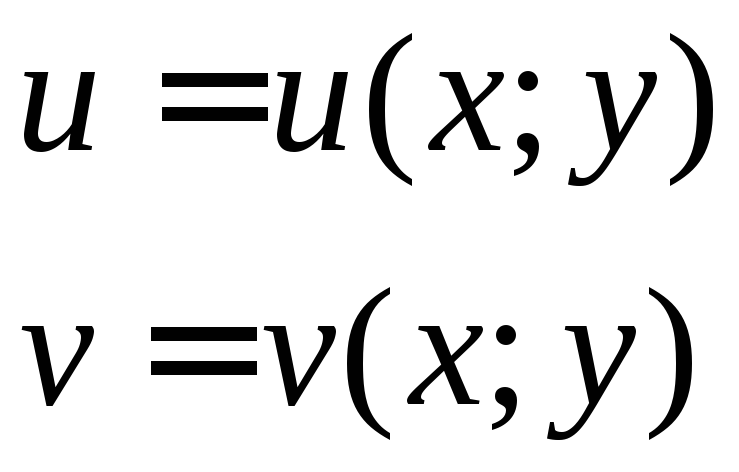
Частные производные
функции
![]() можно найти следующим образом:
можно найти следующим образом:
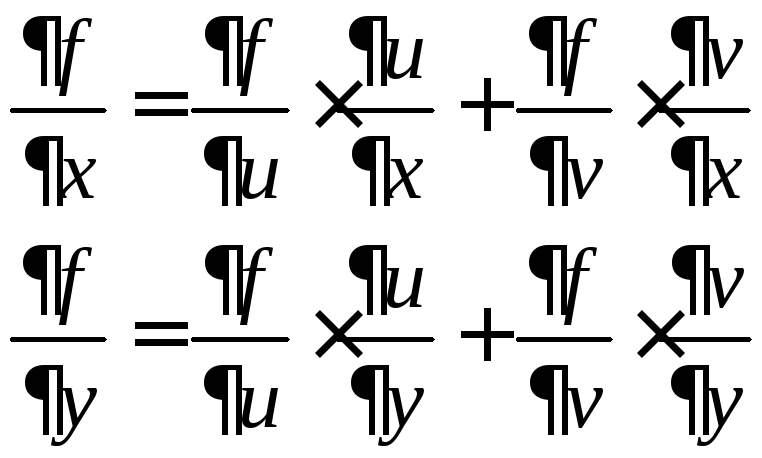
Мнемоническое правило для разыскания частных производных:
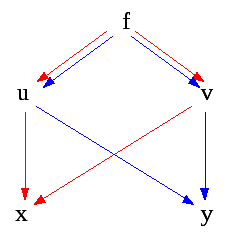
Если функция
зависит от одной переменной, то значок
![]() пишется латинскими буквами, если от
нескольких – греческими:
пишется латинскими буквами, если от
нескольких – греческими:![]() .
.
Пусть имеется
сложная функция
![]() ,
причем функцииu
и v
сами являются ФНП:
,
причем функцииu
и v
сами являются ФНП:
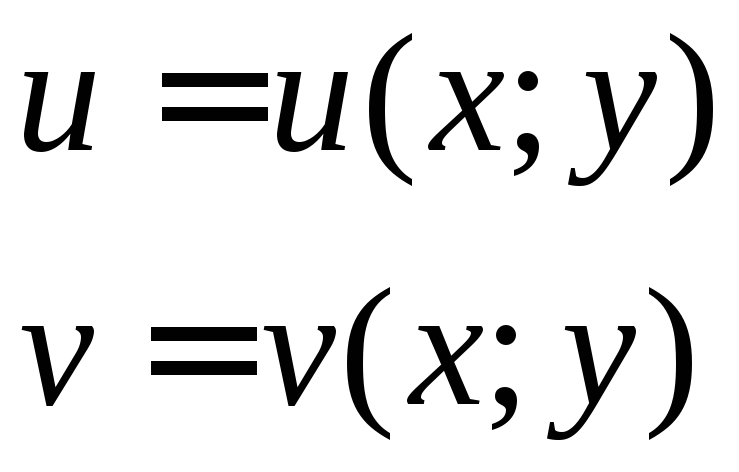
Найдем ее частную производную:
![]()
Пример:
![]()
![]()
![]()
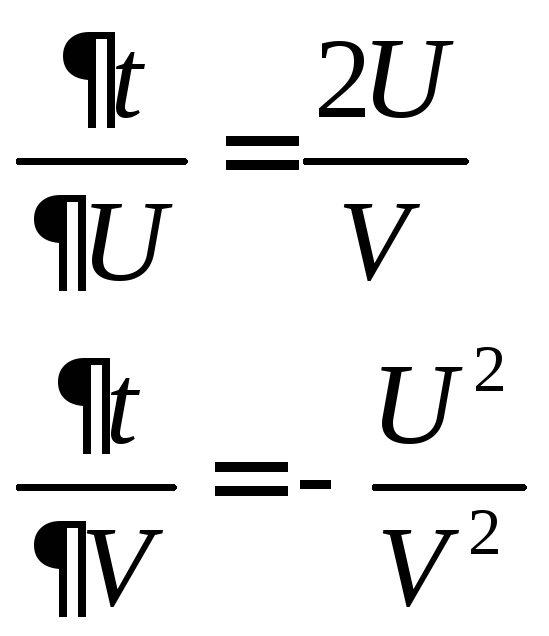
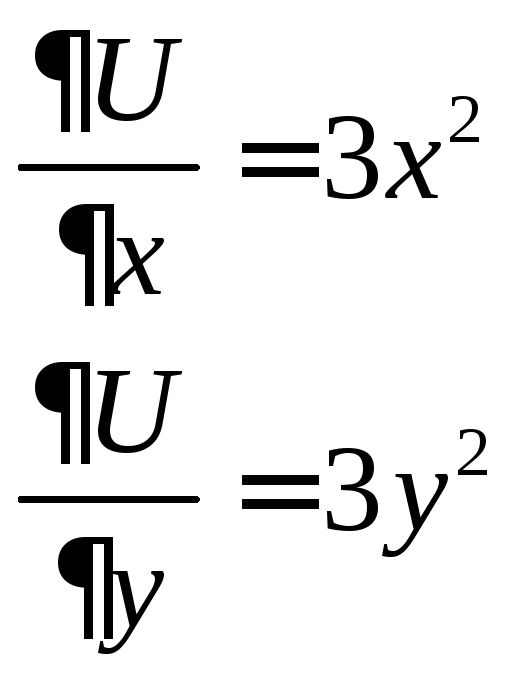
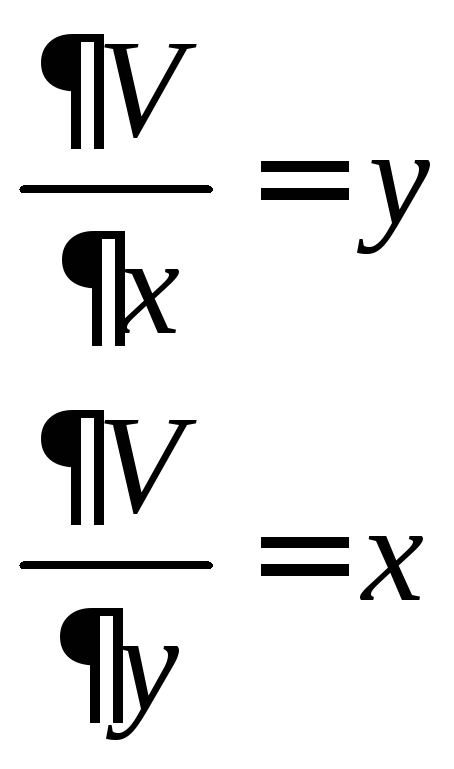
![]()
![]()
Производная неявной ФНП.
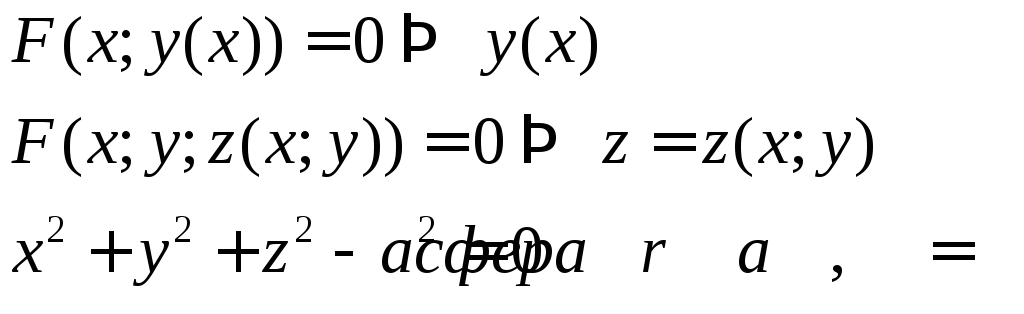
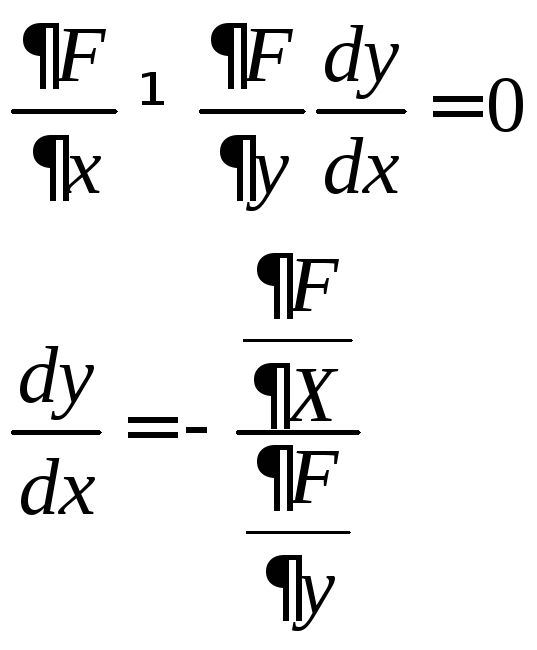
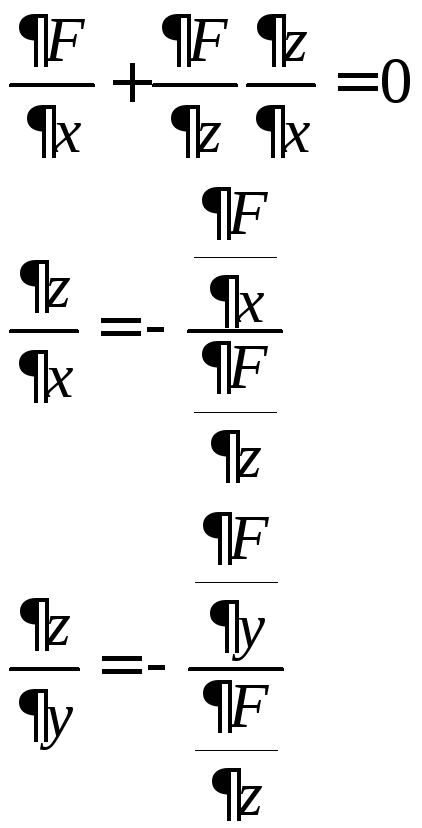
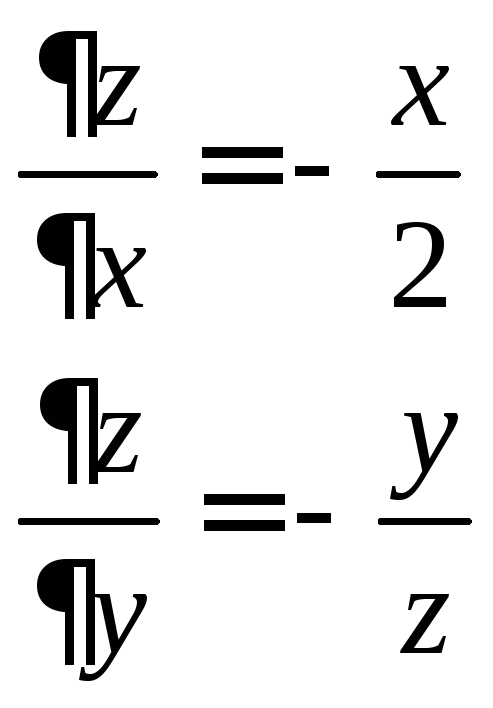
Касательная плоскость и нормаль к поверхности.
Касательная к поверхности - прямая, перпендикулярная к касательной плоскости.
![]()
![]()
![]() -
уравнение касательной плоскости.
-
уравнение касательной плоскости.
Пусть плоскость
задана в виде
![]() =0
=0
Запишем уравнение касательной плоскости и нормали к поверхности.
![]() -
уравнение касательной плоскости.
-
уравнение касательной плоскости.
![]()

Частные производные и полный дифференциал высших порядков ФНП.
Дифференциалы высших порядков.
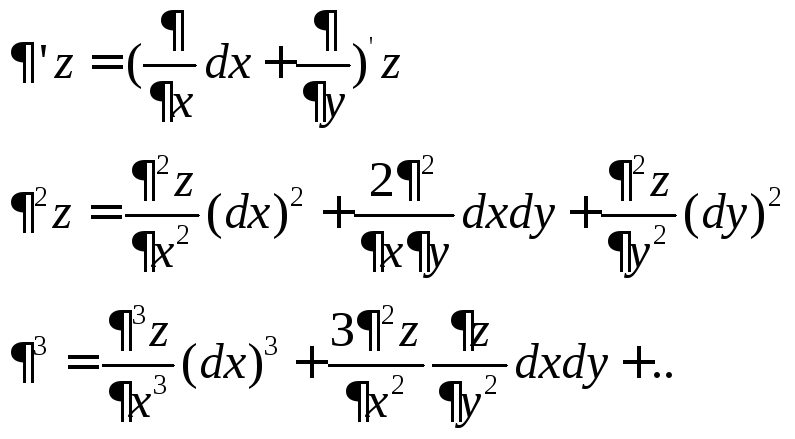
Экстремумы функций нескольких переменных.
Метод множителей Лагранжа.
Нахождение наибольших и наименьших значений ФНП в замкнутой и ограниченной области.
Для ФНП экстремум более сложное понятие, чем для функции одной переменной.
1) Необходимое условие экстремума ФНП.
Пусть имеется
функция
![]() ,
критическими (стационарными) точками
ФНП являются точки в которых:
,
критическими (стационарными) точками
ФНП являются точки в которых:
1) частные производные равны 0 или не существуют
![]() Критические точки
удовлетворяют одной из четырех систем
уравнений:
Критические точки
удовлетворяют одной из четырех систем
уравнений:


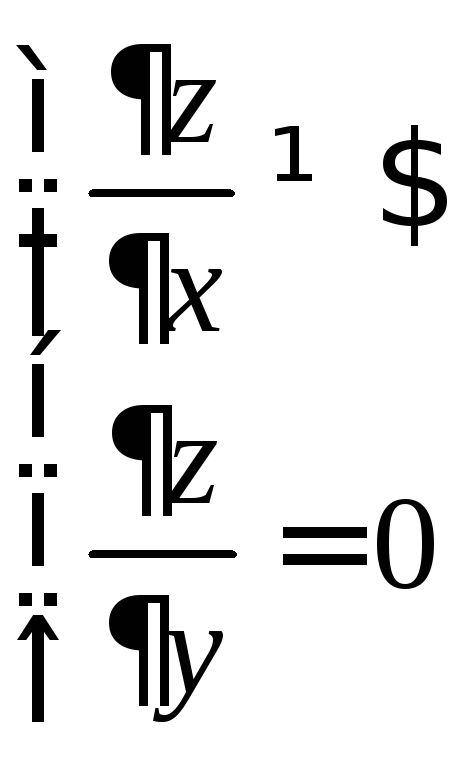
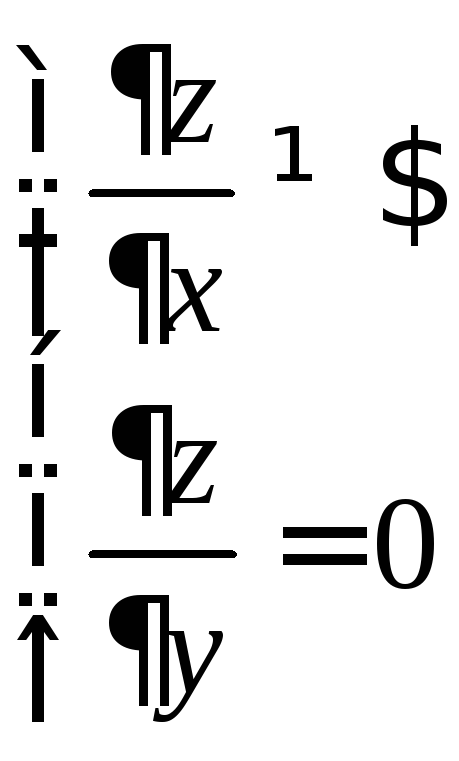
Вообще говоря, точки экстремума находятся среди критических точек, но не каждая является точкой экстремума.
![]()
![]()
![]()
2) Достаточные условия экстремума ФНП
а) Пусть в точках
![]() выполнено условие
выполнено условие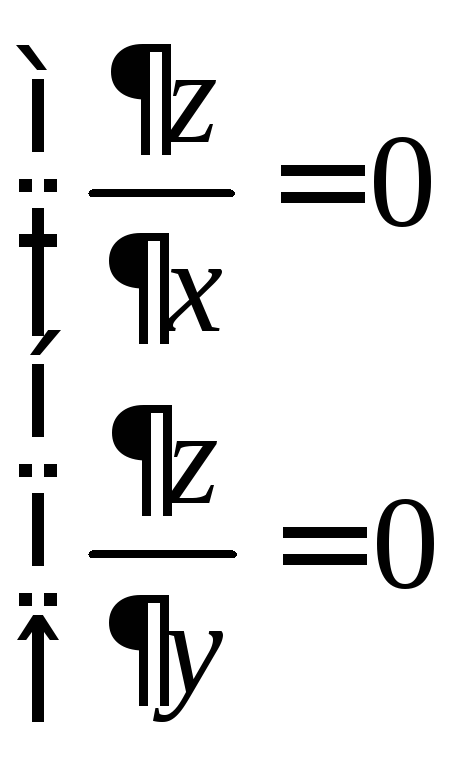 .
Тогда если для точки
.
Тогда если для точки![]() выполнено условие
выполнено условие![]() ,
где
,
где![]()
![]()
![]() ,
то в точки
,
то в точки
![]() экстремум функции двух переменных есть,
причем если А>0, то
экстремум функции двух переменных есть,
причем если А>0, то![]() -точка
минимума, если А<0, то
-точка
минимума, если А<0, то![]() -
точка максимума.
-
точка максимума.
б) Если
![]() ,
то экстремума нет
,
то экстремума нет
в) Если
![]() ,
то требуется дополнительное исследование:
рассмотрение функции по различным
направлениям.
,
то требуется дополнительное исследование:
рассмотрение функции по различным
направлениям.
Если найдены
точки экстремума и
![]() ,
то иногда бывает достаточно сложно
определить что это за экстремум(min/max)
,
то иногда бывает достаточно сложно
определить что это за экстремум(min/max)
![]()
г) Условные экстремумы. Метод множителей Лагранжа.
![]() -функция
НП
-функция
НП
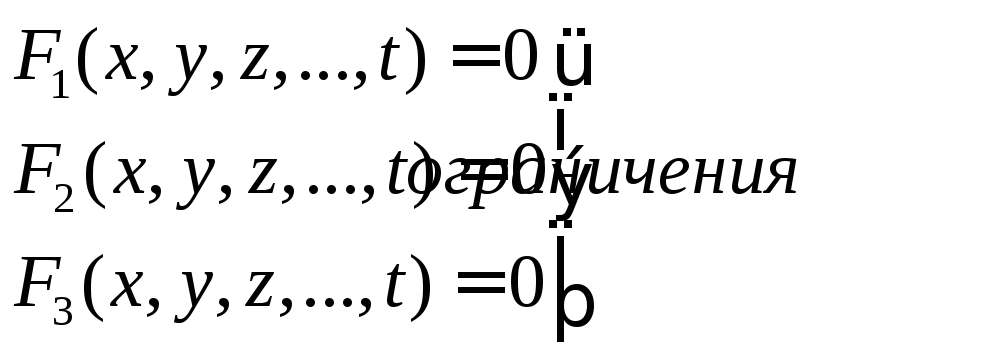
Лагранж предложил метод:
1) Записываем функцию Лагранжа.
![]()
Задача сводится
к нахождению экстремума функции Лагранжа
по переменным
![]()
Метод множителей Лагранжа позволяет задачу (1) свести к задаче схождения экстремума Функции Лагранжа.
4) т. Вейерштрасса
1) Область G называется замкнутой, она содержит все свои границы. Область G – ограниченная, если ее можно поместить внутрь круга (шара) конечного радиуса.
Теорема: Непрерывная функция НП в области G замкнутой и ограниченной достигает своего наибольшего и наименьшего значения. Если функция дифференцируема, то можно найти алгоритм нахождения наибольшего и наименьшего значений в замкнутой ограниченной области.
Область G
задана границами
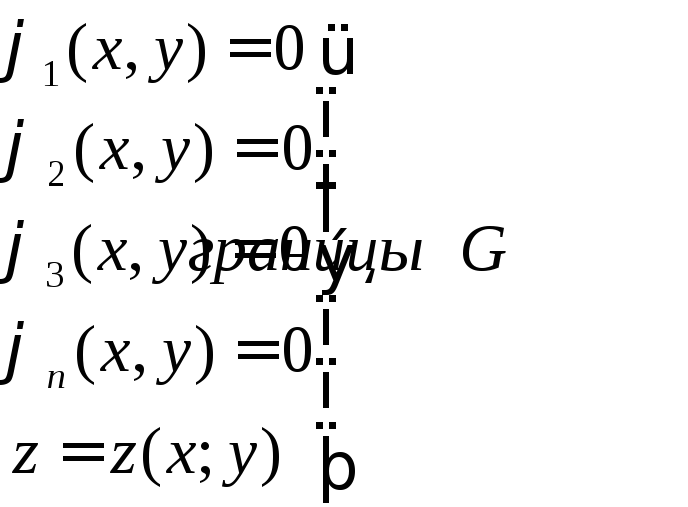
1) находим критические точки
2) выбираем среди них те, внутри области G
3) исследуем функцию 2 на границах
4) выбираем среди критических точек те, которые принадлежат к области G
5) Находим условные
точки – в которых пересекаются
![]() и
и![]()
6) Вычисляем значение функции в полученных точках и находим среди них наибольшие и наименьшие значения.
Дифференциальные уравнения.
Обыкновенные ДУ (ОДУ)
Линейные ДУ и системы ДУ
Обыкновенные и линейные дифференциальные уравнения отличаются по методу решения. Они имеют большое практическое применение.
Литература к курсу:
Теория
1.Петровский «Дифференциальные уравнения» (на «5»).
2.Степанов «Дифференциальные уравнения» (на «4»).
3. Л.А. Адамская «Дифференциальные уравнения и их применение»
Практика
Филлипов «Дифференциальные уравнения и их применение»
Данко, Попов, Кожевников «Высшая математика в упражнениях и задачах»
Методички
Основные понятия теории дифференциальных уравнений.
Общий вид ДУ:
![]() (1)
(1)
Наивысший порядок производной называется порядком дифференциального уравнения.
Решить ДУ – найти зависимость между (вставить)
Функция
![]() называется решением ДУ, если она, будучи
подставлена в ДУ вместе со своими
производными в уравнение (1) обращает
последнее в верное равенство. Общий вид
решения дифференциального уравнения
(1) называется общим решением:
называется решением ДУ, если она, будучи
подставлена в ДУ вместе со своими
производными в уравнение (1) обращает
последнее в верное равенство. Общий вид
решения дифференциального уравнения
(1) называется общим решением:
![]() - общее решение.
- общее решение.
В общем решении ДУ n-го порядка присутствует n произвольных постоянных.
Если функция y(x) записывается неявным образом, то говорят, что решение записывается в виде общего интеграла:
![]()
Задача Коши. Теорема о существовании единственного решения ДУ.
Рассмотрим дифференциальное уравнение 1-го порядка:
![]() (2)
(2)
Пусть
![]() - общее решение ДУ (2),
- общее решение ДУ (2),![]() - общий интеграл (2).
- общий интеграл (2).
Если вместе с ДУ (2) заданы начальные условия:
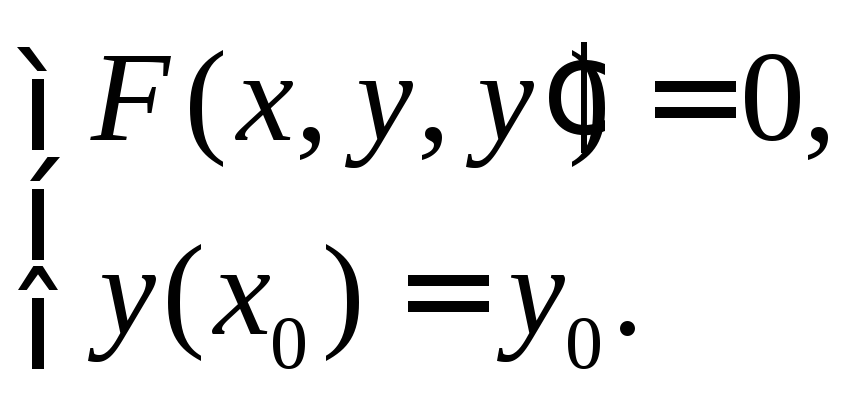 (3),
(3),
то говорят, что для уравнения (2) поставлена задача Коши.
Для уравнения n-го порядка надо поставить n начальных условий:
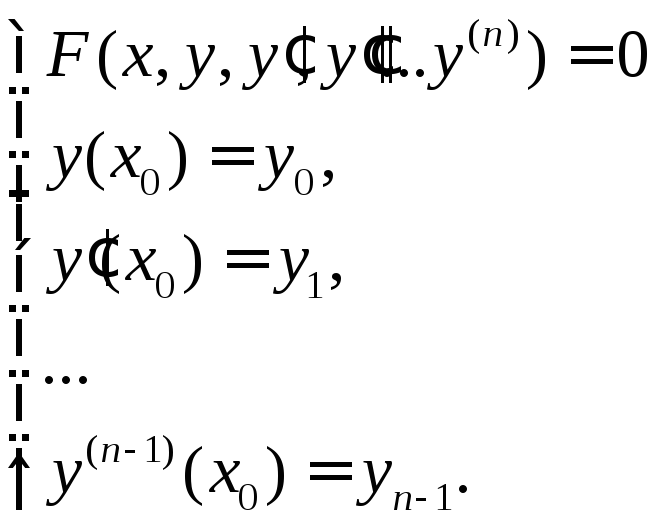 (4),
(4),
Решения задачи
Коши (3) называется частным решением ДУ.
Если решение задачи Коши записывается
в виде
![]() ,
то говорят о частном интеграле.
,
то говорят о частном интеграле.
Теорема о существовании и единственности решения ДУ.
Пусть имеется дифференциальное уравнение (ДУ), разрешенное относительно старшей производной:
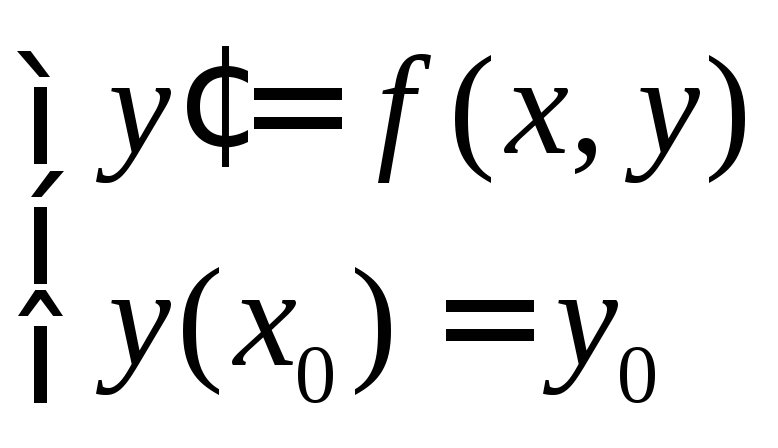 . (5)
. (5)
Предположим, что
функция
![]() задана на замкнутом и ограниченном
множествеD.
Пусть
задана на замкнутом и ограниченном
множествеD.
Пусть
![]() непрерывна везде в этом множестве,
включая его границу, точка
непрерывна везде в этом множестве,
включая его границу, точка![]() лежит внутри этой области. Пусть
лежит внутри этой области. Пусть![]() также непрерывна вD,
тогда задача Коши для (5) имеет единственное
решение.
также непрерывна вD,
тогда задача Коши для (5) имеет единственное
решение.
![]() .
Решение задачи (5) графически изображается
интегральной кривой ДУ.
.
Решение задачи (5) графически изображается
интегральной кривой ДУ.
Следствие:
Так как
![]() непрерывна, то
непрерывна, то![]() ,
следовательно
,
следовательно![]() .
Пример:
.
Пример:![]() .
.
Дифференциальные уравнения с разделяющимися переменными.
Общий вид уравнения:
![]() . (6)
. (6)
Уравнение с
разделенными переменными и если ДУ 1-го
порядка
![]() алгебраическими операциями приводится
к уравнению (6). В уравнении (2) при
разделении переменных
алгебраическими операциями приводится
к уравнению (6). В уравнении (2) при
разделении переменных![]() заменяется на
заменяется на![]() и приводится к уравнению вида (6).Если
не получается, то заданное уравнение
не является уравнением с разделяющимися
переменными.
и приводится к уравнению вида (6).Если
не получается, то заданное уравнение
не является уравнением с разделяющимися
переменными.
Решение уравнения с разделяющимися переменными.
![]()
![]() (7)
- общий интеграл ДУ (6)
(7)
- общий интеграл ДУ (6)
Пример решения ДУ (с разделяющимися переменными):
![]() .
.
![]()
![]()
![]() - общий интеграл
данного ДУ
- общий интеграл
данного ДУ
![]() .
.
![]() - общее решение
данного ДУ.
- общее решение
данного ДУ.
![]()
![]() - решение задачи
Коши.
- решение задачи
Коши.
Однородные ДУ.
Пример:
![]() - данное уравнение
не относится к уравнениям с разделяющимися
переменными.
- данное уравнение
не относится к уравнениям с разделяющимися
переменными.
![]()
Функция
![]() называется однороднойm-го
измерения, если выполняется условие:
называется однороднойm-го
измерения, если выполняется условие:
![]() .
.
Пример:
![]() - однородная, 1-го
измерения
- однородная, 1-го
измерения
![]() -
однородная, 2-го измерения
-
однородная, 2-го измерения
![]() - неоднородная
функция
- неоднородная
функция
![]() - неоднородная
функция
- неоднородная
функция
Однородные дифференциальные уравнения.
Дифференциальное
уравнение
![]() называется
однородным, если функции
называется
однородным, если функции![]() и
и![]() являются однородными функциями одинаковых
измерений или если уравнение разрешено
относительно старшей производной
являются однородными функциями одинаковых
измерений или если уравнение разрешено
относительно старшей производной![]() ,
то
,
то![]() является однородной функцией 0-го
измерения.
является однородной функцией 0-го
измерения.
![]()
![]()
![]()
Для решения
однородных уравнений используется
замена
![]() ,
откуда найдем:
,
откуда найдем:
![]()
![]()
![]()
Пример решения однородного ДУ:
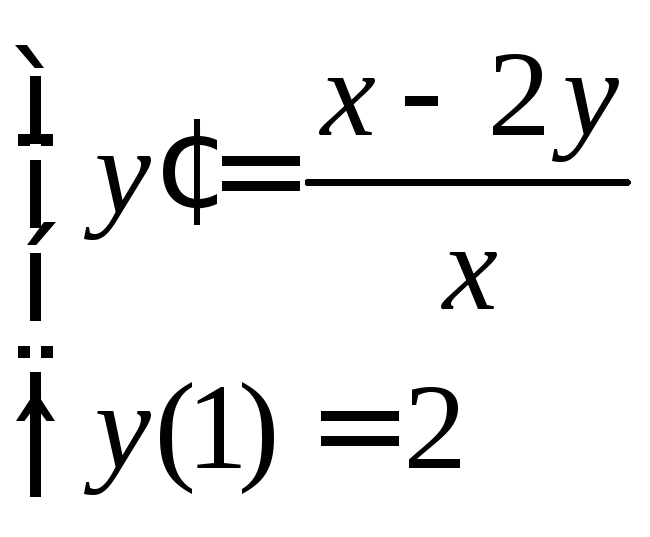 -
задача Коши.
-
задача Коши.
![]()
![]()
![]()
![]()
![]()
Найдем постоянную интегрирования C исходя из начальных условий:
![]()
![]()
![]()
![]()
![]()
Линейные дифференциальные уравнения 1-го порядка. Уравнения Бернулли. Дифференциальные уравнения, допускающие понижение порядка.
ДУ вида
![]() называются линейными дифференциальными
уравнениями.
называются линейными дифференциальными
уравнениями.
Пример:
![]() .
.
Переходные процессы в линейных электрических цепях.
![]() - уравнение
переходного процесса.
- уравнение
переходного процесса.
Решение ЛДУ:
ЛДУ решается с
помощью представления искомой функции
![]() в виде произведения двух функций:
в виде произведения двух функций:![]() .
Производная
.
Производная![]() .
Далее составляется система уравнений,
из которых и находятся искомые функцииu
и v.
.
Далее составляется система уравнений,
из которых и находятся искомые функцииu
и v.
Покажем на примере уравнения переходного процесса решение ЛДУ.
![]()
Подставим в исходное ДУ.
![]()
Сгруппируем
слагаемые с
![]() и
и
![]() :
:
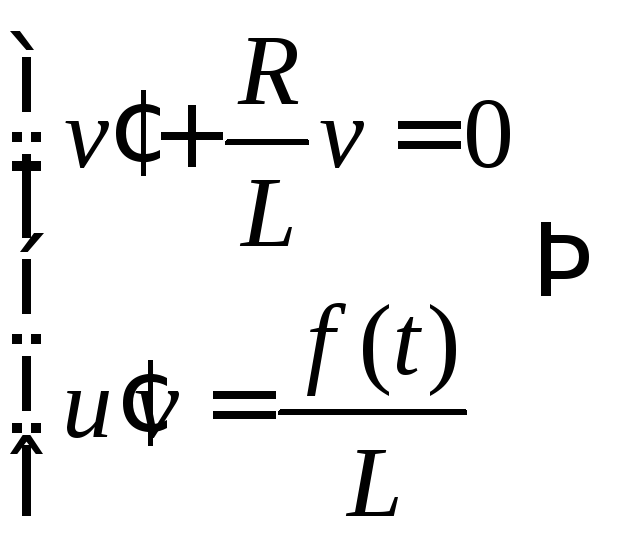
![]()
![]()
![]()
![]()
При нахождении функции v прибавлять постоянную интегрирования C не надо.
![]()

При нахождении функции u прибавлять постоянную интегрирования C надо!

Предположим, что
переходный процесс в цепи начался при
токе в катушке
![]() :
:
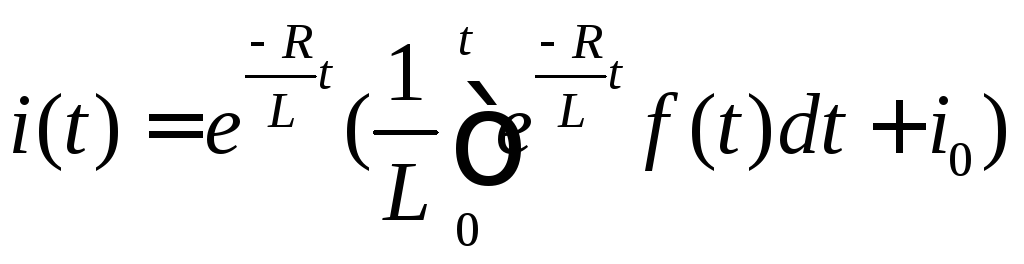
Если в момент
включения цепи
![]() ,
,
![]()

Уравнение Бернулли.
Дифференциальное
уравнение, которое можно привести к
виду
![]() .
.![]() ,
,![]() называется уравнением Бернулли. Оно
интегрируется абсолютно также, как и
ЛДУ. Решением уравнения Бернулли может
быть и
называется уравнением Бернулли. Оно
интегрируется абсолютно также, как и
ЛДУ. Решением уравнения Бернулли может
быть и![]() (особое решение).
(особое решение).
![]()
Найдем общий
интеграл данного ДУ. Положим
![]() ,
тогда
,
тогда![]() .
Для нахождения функции
.
Для нахождения функции![]() берем слагаемые с
берем слагаемые с![]() :
:
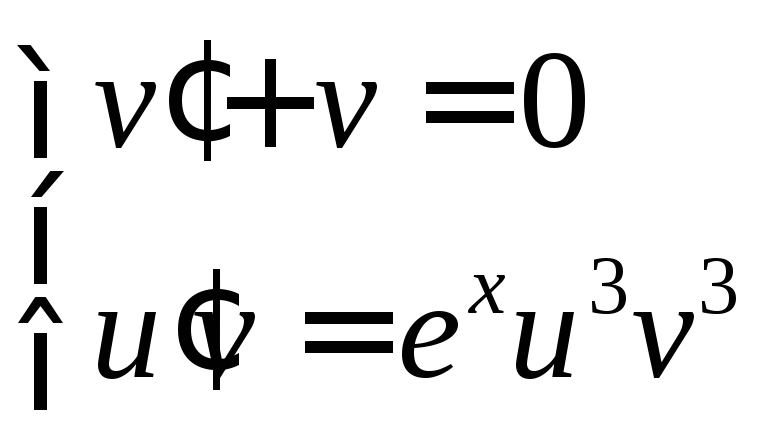
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Вернемся к переменной y:
![]()
Общее решение дифференциального уравнения – частный случай общего интеграла.
Дифференциальные уравнения, допускающие понижение порядка
1)
ДУ вида
![]() .
.![]() нужно проинтегрироватьn
раз.
нужно проинтегрироватьn
раз.
![]()
Пример:
![]() (
(![]() - уск. своб. падения);
- уск. своб. падения);
![]() ;
;
![]() .
.
![]() ,
,
![]() ,
,![]() .
.
2)
Уравнение, не содержащее функцию y(x).
Уравнение имеет след. вид:
![]() .
Делается замена
.
Делается замена![]() ,
,![]() .
.
3)
ДУ явно не зависит от x.
![]() .
Рассматриваем
.
Рассматриваем![]() как функцию свободной переменнойy.
как функцию свободной переменнойy.
![]() ;
;![]() ,
где
,
где
![]() и
и
![]() - функции от
- функции от
![]() .
Интегрируем. Получаем
.
Интегрируем. Получаем![]() ,
,![]()
![]() .
.
Линейные ДУ (ЛДУ) высших порядков
Определение.
Линейным
дифференциальным уравнением
высшего порядка называется уравнение
вида
![]() (1)
(1)
Пусть
![]() - решение (1).ДУ
называется однородным, если
- решение (1).ДУ
называется однородным, если
![]() ,
и неоднородным в противном случае.
Замечание: пусть
,
и неоднородным в противном случае.
Замечание: пусть![]() ,
,![]() - нек. решения однородного ЛДУ
- нек. решения однородного ЛДУ
![]() ,
тогда
,
тогда
![]() также является решением уравнения (2).
также является решением уравнения (2).
Линейная зависимость. Линейная независимость функций.
N
функций y1(x),
y2(x),
..., yn(x)
называются линейно зависимыми, если
существуют такие константы С1,
С2,
…, Сn,
не все равные 0, что
![]() .
В противном случае система функций
называется линейно независимой (для
всехx
из обл. опр.).
.
В противном случае система функций
называется линейно независимой (для
всехx
из обл. опр.).
Пусть
![]() ,
,![]() , тогда 1 ф-ю можно выразить через
остальные.
, тогда 1 ф-ю можно выразить через
остальные.![]() ;
;![]() ,
,![]() ;
-const
;
-const
Если ф-и лин. независимы, то их отношение не является постоянной.
![]() ,
,
![]() ;
;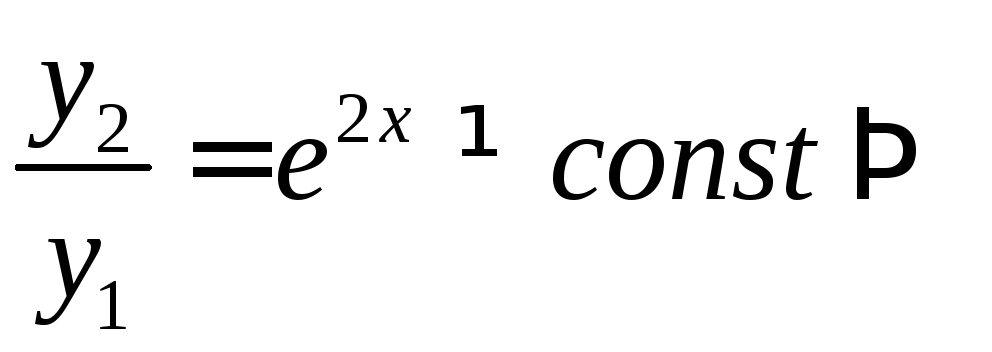 лин.
незав.
лин.
незав.
![]() ,
,![]() ;
;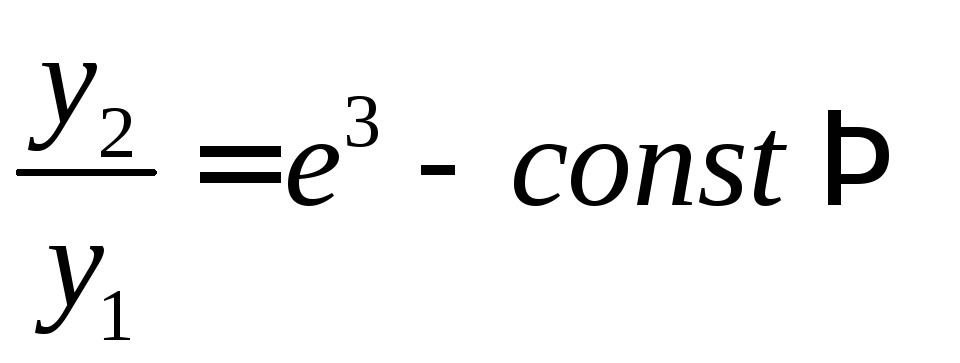 лин. зав.
лин. зав.
![]() .
.
Критерий линейной зависимости и линейной независимости решения линейных однородных ДУ. Определитель Вронского.
Пусть
y1,
y2,
..., yn
– сист. ф-й, опред на
![]() ,
имеющ на
,
имеющ на![]() (n-1)
производных.
(n-1)
производных.
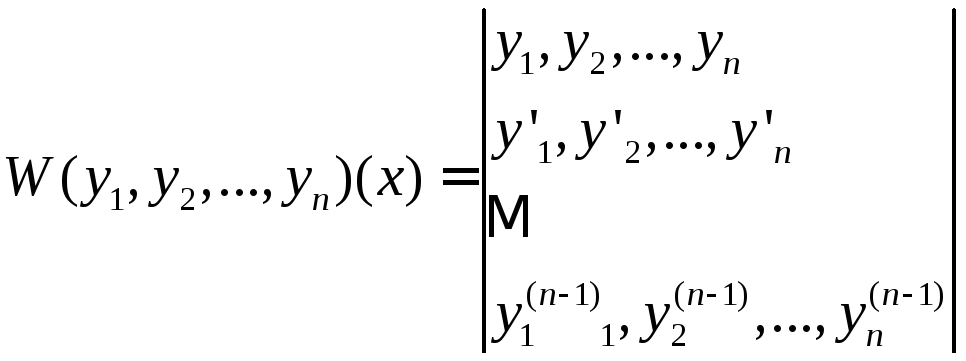 Определитель
Вронского.
Определитель
Вронского.
Из
свойств определителей, линейности
произв. любого порядка и определения
линейной зависимости следует, что для
совокупности линейно зависимых на
![]() функций определитель Вронского
функций определитель Вронского![]() .
.
Критерии:
пусть y1,
y2,
..., yn
– решения ЛОДУ
![]() на
на![]() ,
тогда эти решения линейно независимы
тогда и только тогда, когда их определитель
Вронского
,
тогда эти решения линейно независимы
тогда и только тогда, когда их определитель
Вронского![]() .
.
ЛОДУ высших порядков с постоянными коэффициентами.
Общее
решение ЛОДУ:
![]() .
.
y1(x),
y2(x),
..., yn(x)
– независим. совок. решений ЛОДУ
![]() .
.
В этом случае можем найти решение в элементарных функциях. a1, a2, …, an – const;
![]()
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;![]()
![]() ;
;![]() (2)
(2)
(2)
и
![]() - характеристические уравнения для (1)
и
- характеристические уравнения для (1)
и
![]() .
.
Нахождение общего решения ЛОДУ с постоянными коэффициентами для уравнения второго порядка. Блок схема решения.
![]() ;
;
![]() (1)
(1)
1)
корни характеристического уравнения
(1) действительны и различны:
![]() ;
;![]() ;
;![]() ;
;![]() ;
С1
и С2
– const.
;
С1
и С2
– const.
2)
![]() ;
;
![]() ;
;![]() ;
;![]()
3)
![]() ;
;![]() ;
;![]() ;
;![]()
Теорема о структуре решения ЛНДУ.
![]() (1). Пусть (1) –
линейное неоднородное дифференциальное
уравнение, тогда общее решение записывается
в виде суммы общих решений однородного
уравнения
(1). Пусть (1) –
линейное неоднородное дифференциальное
уравнение, тогда общее решение записывается
в виде суммы общих решений однородного
уравнения
![]() (2) и частного решения уравнения (1).
(2) и частного решения уравнения (1).
![]() (3). Докажем, что
произвольное решение y
уравнения (1) можно записать в форме (3).
(3). Докажем, что
произвольное решение y
уравнения (1) можно записать в форме (3).
![]() - некоторое найденное фиксированное
решение уравнения (1). Рассмотрим разность
- некоторое найденное фиксированное
решение уравнения (1). Рассмотрим разность![]() - решение однородного уравнения (2).
- решение однородного уравнения (2).![]() - некоторое решение уравнения (1).
- некоторое решение уравнения (1).
![]() .
.
ЛНДУ
с постоянными коэффициентами и специальным
видом правой части
![]() .
.
![]() ,
где
,
где
![]() - многочленn-й
степени,
- многочленn-й
степени,
![]() .
Задача нахождения общего решения
фактически сводится к задаче нахождения
.
Задача нахождения общего решения
фактически сводится к задаче нахождения![]() .
.
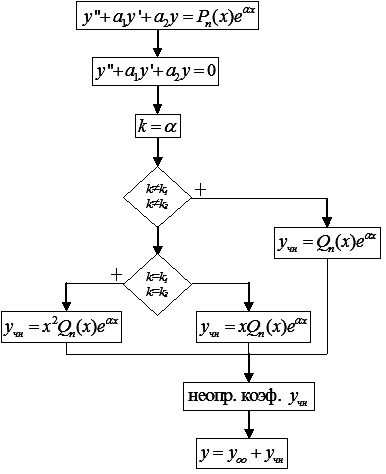
Замечания:
1)
эта блок-схема позволяет решить уравнение,
в правой части которого многочлен
![]() .
.
2)
Виды многочлена
![]() :
:
![]() ;
;
![]() ;
;
![]() .
.
Линейные
неоднородные дифференциальные уравнения
с постоянными коэффициентами и специальным
видом правой части
![]() .
.
![]() ,
,
![]() ;
;
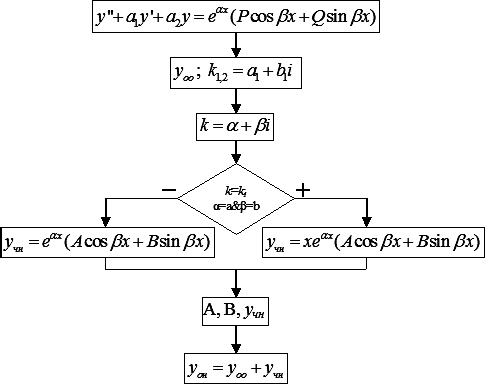
Теорема наложения.
Рассмотрим
ДУ
![]() .
.![]() и
и![]() могут зависеть от
могут зависеть от![]() ,
тогда частное решение этого уравнения
представляет собой сумму частных решений
уравнений
,
тогда частное решение этого уравнения
представляет собой сумму частных решений
уравнений![]() и
и![]() .
Доказательство следует из линейности
производных.
.
Доказательство следует из линейности
производных.
Колебательный контур.
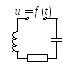
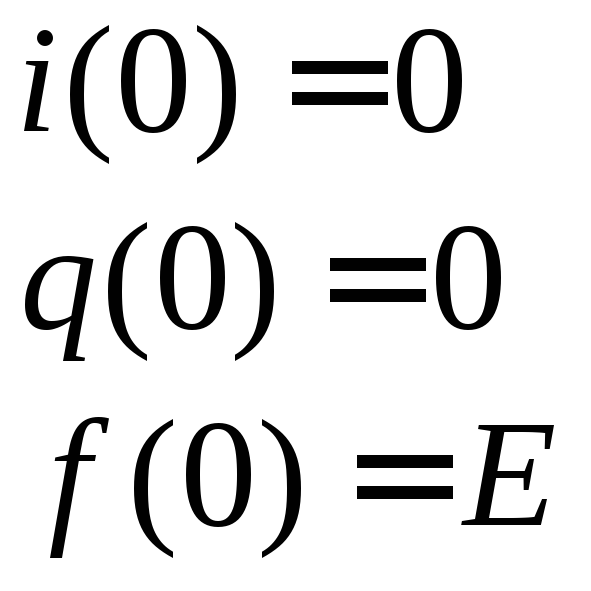
По
второму закону Кирхгофа составим
дифференциальное уравнение для данной
схемы: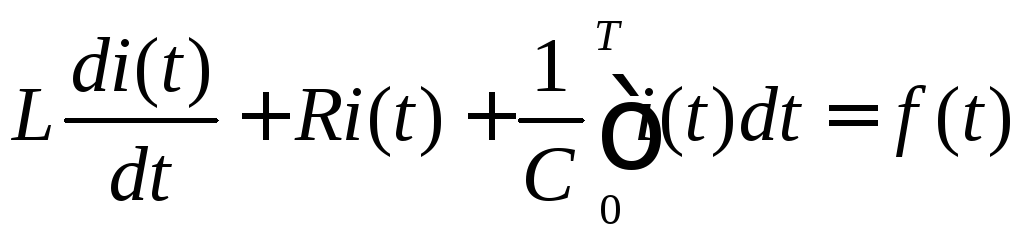 (1).
(1).
Из
курса физики известны следующие
соотношения:
![]() ,
,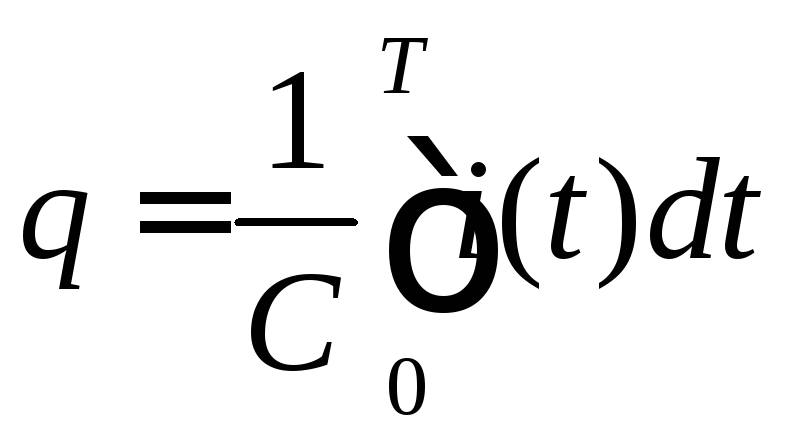
Продифференцируем (1) и введем следующие обозначения.
![]() ;
;
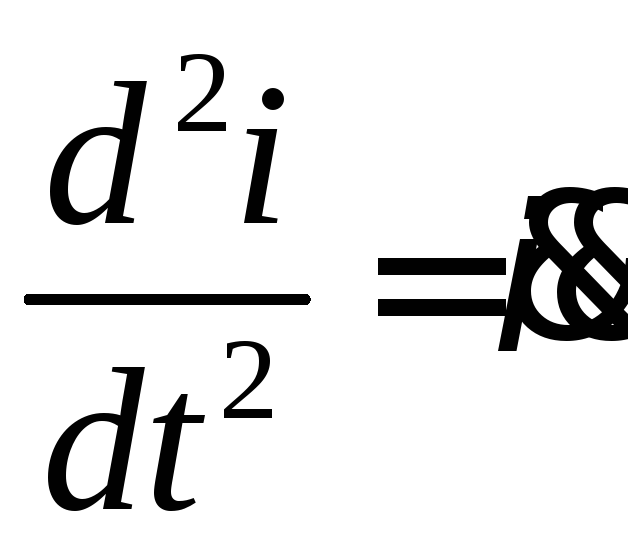 ;
;![]() (2)
(2)
Пусть
![]() - величина постоянная, равнаяE
(контур включается на постоянное
напряжение),
- величина постоянная, равнаяE
(контур включается на постоянное
напряжение),
![]() (1) превращается в однородное уравнение:
(1) превращается в однородное уравнение:![]()
Характеристическое уравнение:
![]() ;
;
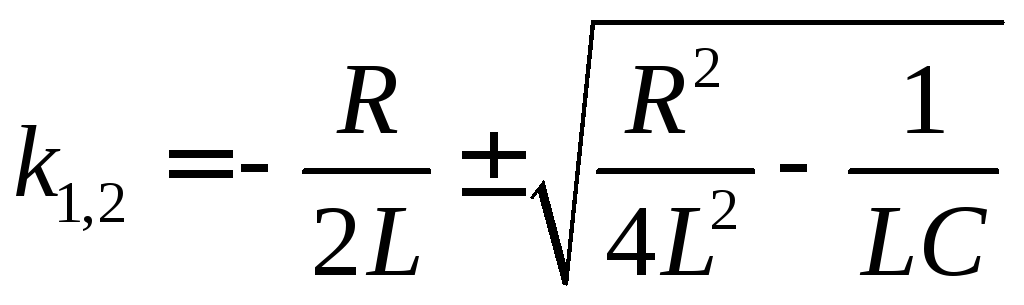 .
.
Рассмотрим различные случаи (в зависимости от начальных параметров):
1)
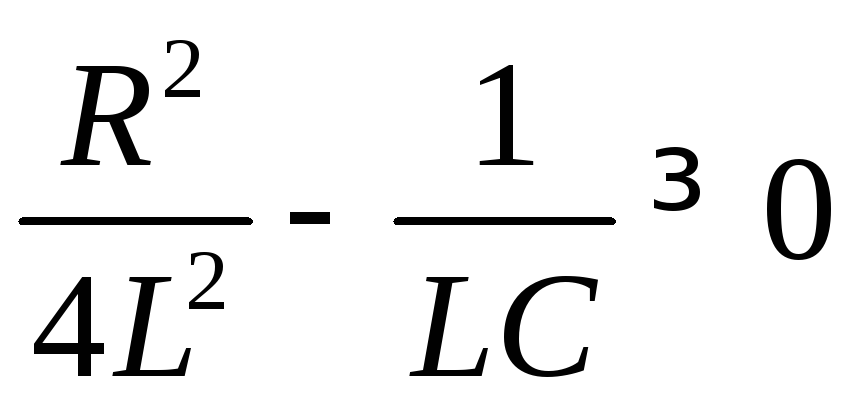 ;
;![]() ;
;![]() ;
;![]()

2)
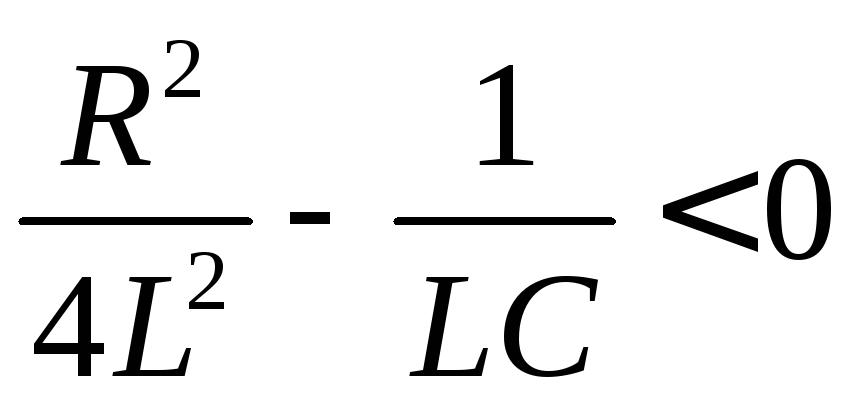 ;
;
 ;
;![]() ;
;
![]()
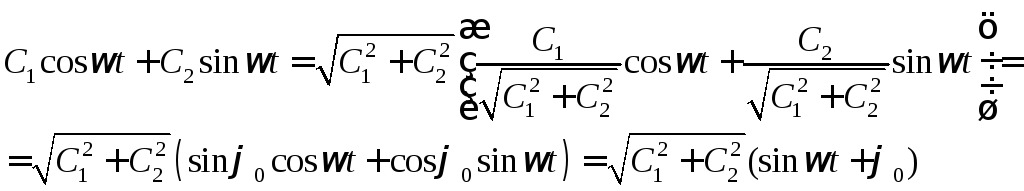
Если на колебательный контур подается постоянное напряжение, то получаются затухающие колебания (ударное возбуждение контура).
Рассмотрим практически важный случай - подключение колебательного контура к источнику синусоидального напряжения:
![]() ;
;
![]() ;
;![]() ;
;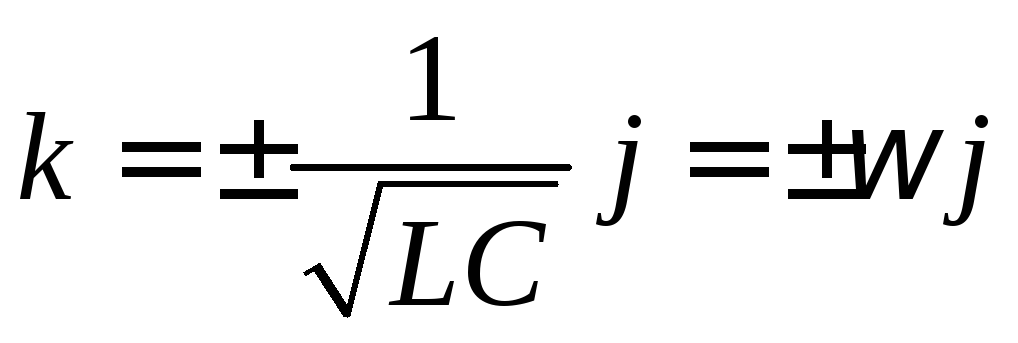
![]() ;
А – амплитуда гармонических колебаний,
;
А – амплитуда гармонических колебаний,
![]() - круговая частота,
- круговая частота,![]() - начальная фаза.
- начальная фаза.
1)
![]() ;
;![]() ;
;![]() - нерезонансный случай;
- нерезонансный случай;
2)
![]() ;
;![]() - резонансный случай.
- резонансный случай.
Системы ДУ. Нормальная система дифференциальных уравнений. Линейная система дифференциальных уравнений.
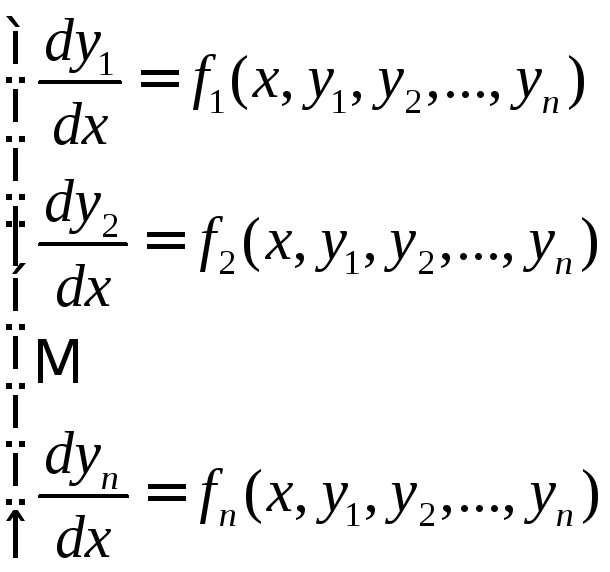
Система дифференциальных уравнений – совокупность ДУ. Система n ДУ 1-го порядка, разрешенных относительно всех производных, называется нормальной и имеет вид (1):
В
этой системе
![]() - это неизвестные функции от независимой
переменнойx.
- это неизвестные функции от независимой
переменнойx.
![]() - это известные функции.
- это известные функции.![]() определена и непрерывна в некоторой
области. Если правые части уравнений
системы (1) являются линейными функциями
от функций
определена и непрерывна в некоторой
области. Если правые части уравнений
системы (1) являются линейными функциями
от функций![]() ,
то система ДУ называется линейной.
,
то система ДУ называется линейной.
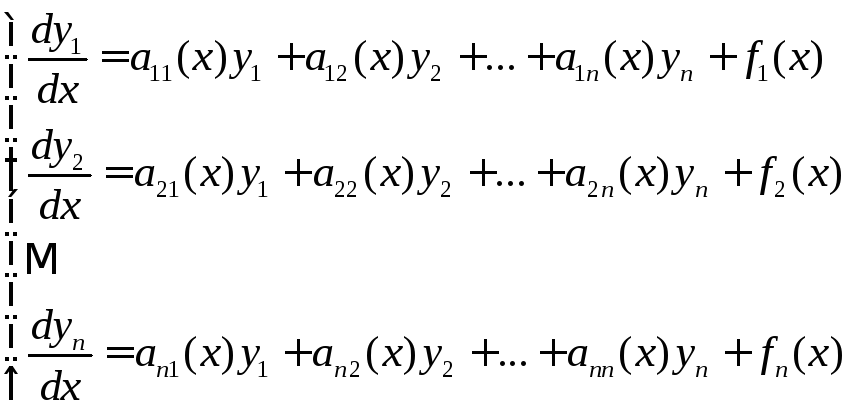 (2)
(2)
Если
![]() ,
то (2) – линейная однородная система
дифференциальных уравнений, если
,
то (2) – линейная однородная система
дифференциальных уравнений, если![]() ,
то (2) – линейная неоднородная система
дифференциальных уравнений.
,
то (2) – линейная неоднородная система
дифференциальных уравнений.
Задача Коши для системы дифференциальных уравнений. Общее и частное решения систем дифференциальных уравнений. Методы решения систем дифференциальных уравнений.
Задача
Коши состоит в нахождении решений
![]() ,
удовлетворяющих начальным условиям
,
удовлетворяющих начальным условиям![]() .
Геометрический смысл задачи Коши: найти
среди всех интегральных кривых те,
которые проходят через данные точки
.
Геометрический смысл задачи Коши: найти
среди всех интегральных кривых те,
которые проходят через данные точки![]() .
.
Общим решением система дифференциальных уравнений называется совокупность n функций:
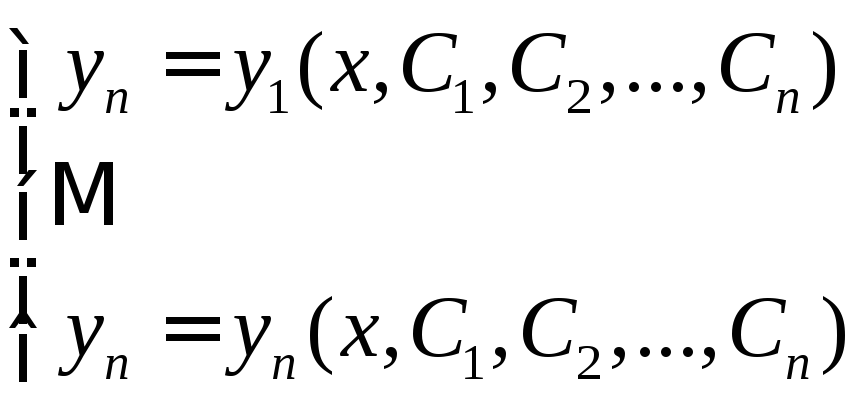 ,
,
и удовлетворяющая следующим условиям:
1)
функции
![]() определены в области изменения переменных
и имеют непрерывные производные поx.
определены в области изменения переменных
и имеют непрерывные производные поx.
2)
функции
![]() должны являться решением система
дифференциальных уравнений для любогоconst
должны являться решением система
дифференциальных уравнений для любогоconst
![]() .
.
Частным
решением система дифференциальных
уравнений называе решение, полученное
из общ. решения при некоторых частных
значениях пост. величин
![]() .
.
система
дифференциальных уравнений (1) сожжет
быть приведена к 1-му ДУ n-го
порядка
![]() ,
и наоборот, ДУn-го
порядка можно свести к система
дифференциальных уравнений.
,
и наоборот, ДУn-го
порядка можно свести к система
дифференциальных уравнений.
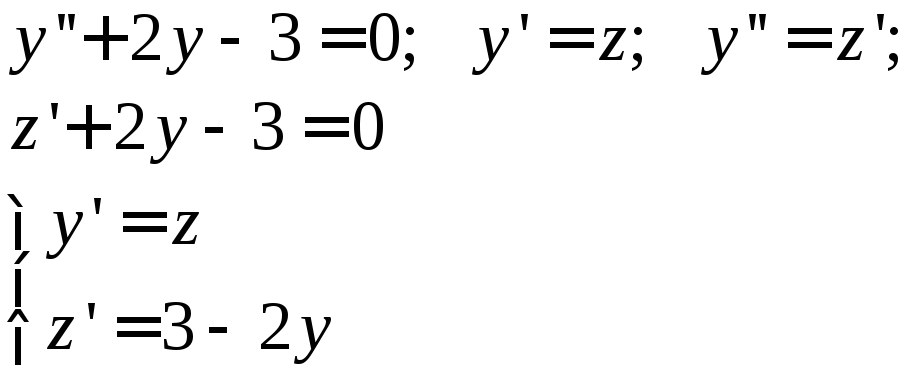

Метод интегрируемых комбинаций.
Уравнения сводят к такому виду, что их легко можно проинтегрировать, откуда находят решение.
Пример:
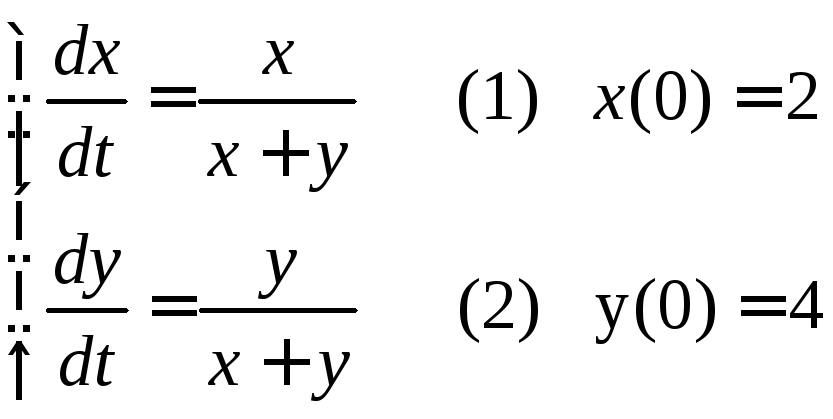
1)
Найдем
![]() .
Разделим (2) на (1):
.
Разделим (2) на (1):

![]()
2) Сложим (1) и (2):
![]()
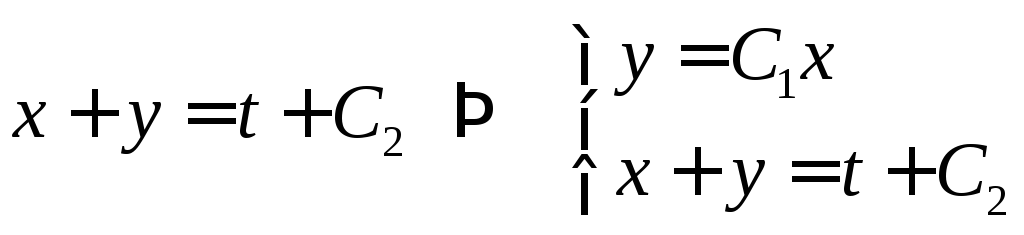
![]()
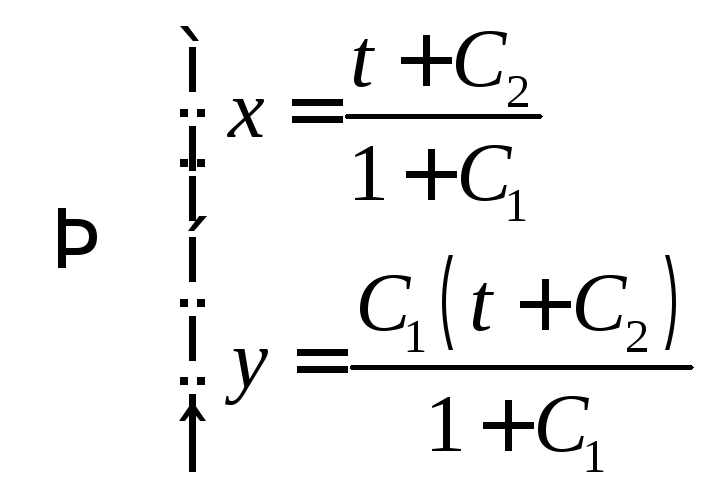 - общее решение
системы
- общее решение
системы
3) Подставляем начальные условия:

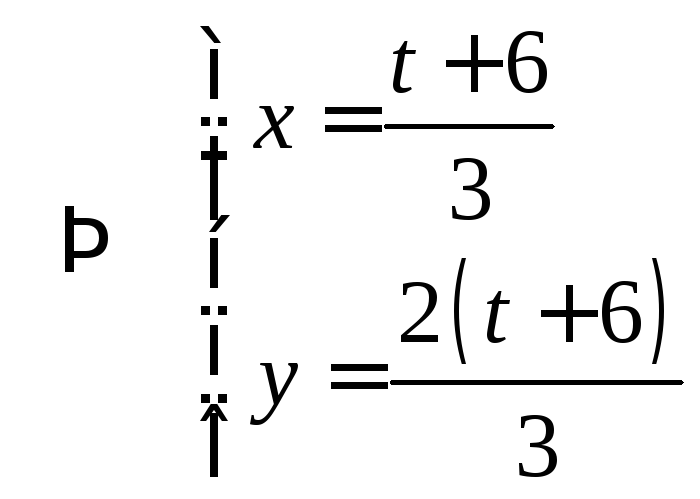 - частное решение
- частное решение
Метод решения систем дифференциальных уравнений средствами алгебры.
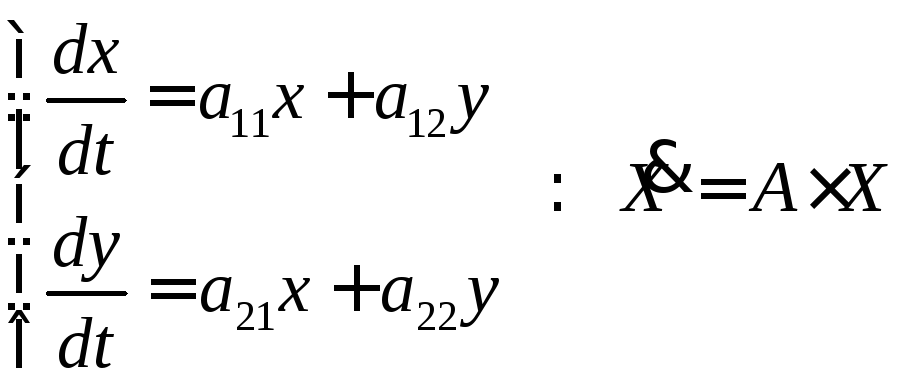 ,
А – основная матрица системы.
,
А – основная матрица системы.
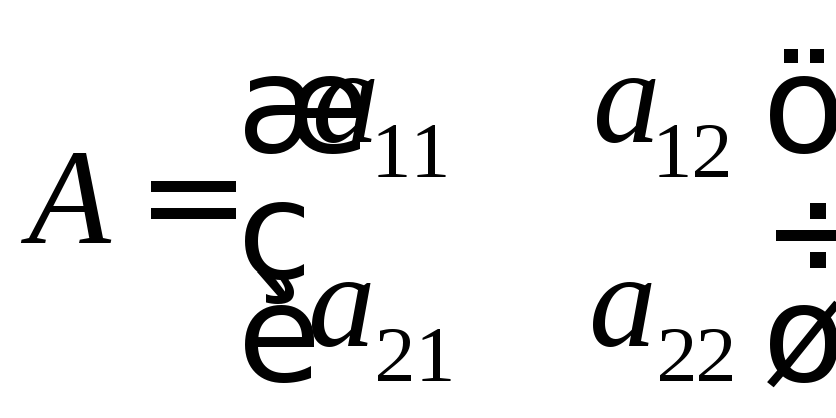 ;
;
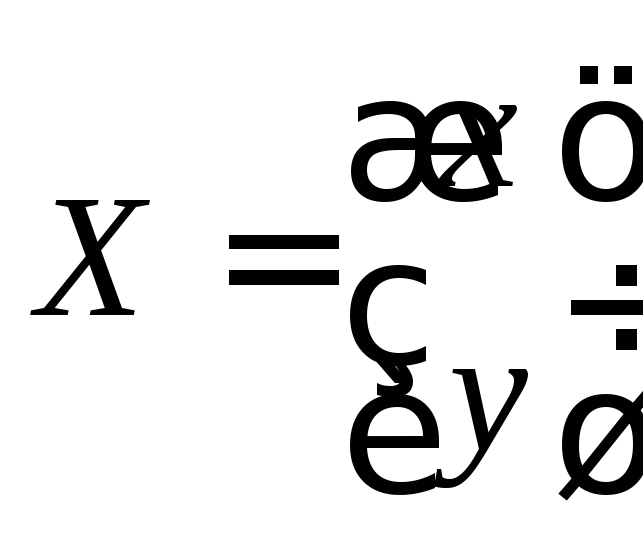 ;
;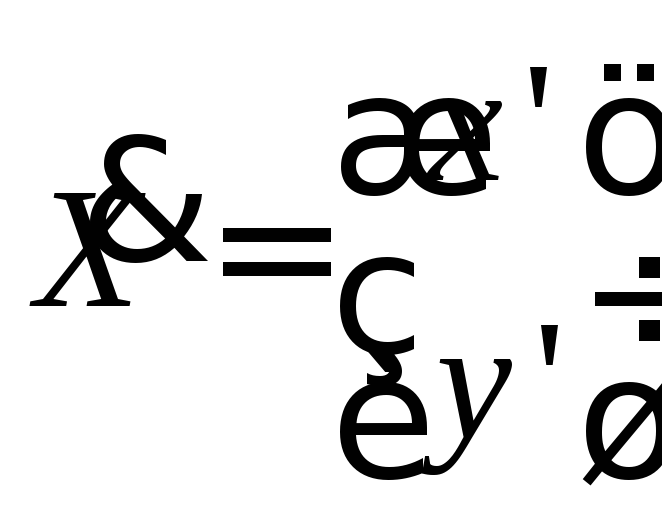 ;
;
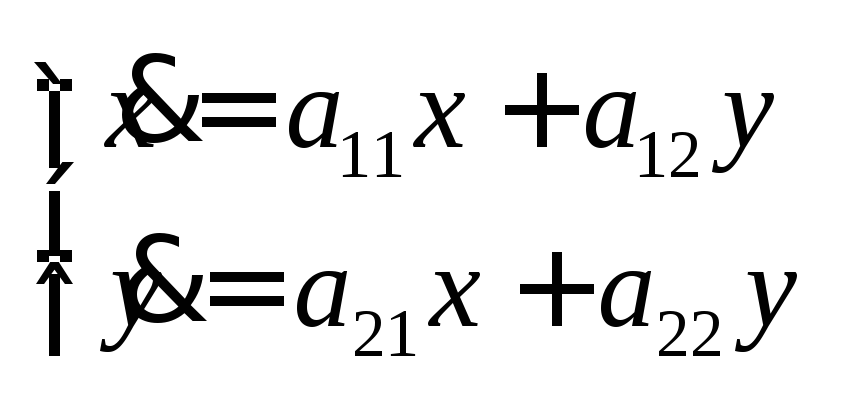 ;
;
![]()
![]()
![]()
![]() ;
;
![]() ;
;
![]() - след матрицы;
- след матрицы;
![]() - ЛОДУ 2-го порядка
- ЛОДУ 2-го порядка
Приложение.
