
- •1) По виду знаменателя находим разложение на простейшие дроби
- •Примеры
- •Примеры
- •2.7. Замена переменной в определенном интеграле
- •Примеры
- •2.8 Несобственные интегралы
- •2.8.1. Интегралы с бесконечными пределами (несобственные интегралы I рода)
- •Примеры
- •2.8.2. Несобственные интегралы от неограниченных функций (несобственные интегралы II рода)
- •Примеры
- •2.9. Вычисление площади плоской фигуры
- •2.9.1. Площадь фигуры, ограниченной графиками непрерывных функций
- •2.9.2. Площадь фигуры, ограниченной кривой, заданной параметрически
- •Вспомогательная таблица для построения параметрически заданной кривой
- •2.9.3. Площадь фигуры, ограниченной кривой, заданной в полярных координатах
- •Вспомогательная таблица для построения кривой, заданной в полярных координатах
- •Функции многих переменных
- •Линии и поверхности уровня
- •1. Решить линейные однородные дифференциальные уравнения.
- •3. Решить линейные неоднородные дифференциальные уравнения.
- •4. Найти решение задачи Коши для системы линейных дифференциальных уравнений.
- •5. Найти общее решение системы линейных дифференциальных уравнений.
Примеры
1)
![]() .
Подынтегральная функция
.
Подынтегральная функция![]() и первообразная непрерывны на промежутке
интегрирования, поэтому формулой
Ньютона-Лейбница пользоваться можно:
и первообразная непрерывны на промежутке
интегрирования, поэтому формулой
Ньютона-Лейбница пользоваться можно:![]() .
.
2)
 .
Подынтегральная функция
.
Подынтегральная функция![]() и первообразная непрерывны на промежутке
интегрирования, поэтому
и первообразная непрерывны на промежутке
интегрирования, поэтому .
.
3)
![]() .
Здесь подынтегральная функция
.
Здесь подынтегральная функция![]() терпит
разрыв в точке
терпит
разрыв в точке![]() .
Поэтому формулой Ньютона-Лейбница в
данном примере воспользоваться нельзя,
однако выражения такого типа имеют
определенный смысл, который рассмотрим
в дальнейшем.
.
Поэтому формулой Ньютона-Лейбница в
данном примере воспользоваться нельзя,
однако выражения такого типа имеют
определенный смысл, который рассмотрим
в дальнейшем.
Интегрирование по частям в определенном интеграле
Если функции
![]() и их производные
и их производные![]() непрерывны на отрезке
непрерывны на отрезке![]() ,
то имеет место формула интегрирования
по частям в определенном интеграле.
,
то имеет место формула интегрирования
по частям в определенном интеграле.
![]() (27)
(27)
Порядок вычисления:
все подынтегральное выражение разбить на две части, одну обозначить символом
 ,
другую -
,
другую - (см. п. 1.5);
(см. п. 1.5);вычислить дифференциал
 функции
функции и найти функцию
и найти функцию по ее дифференциалу, интегрируя
по ее дифференциалу, интегрируя ;
;применить формулу интегрирования по частям, проверив предварительно непрерывность функций
 .
.
Формула интегрирования по частям применяется для тех же типов интегралов, что описаны в п. 1.5.
Примеры
1)


![]() .
.

![]() .
.
Отметим, что
поскольку функции
![]() и
и![]() непрерывны на
непрерывны на![]() ,
формулой интегрирования по частям
пользоваться можно.
,
формулой интегрирования по частям
пользоваться можно.
2.7. Замена переменной в определенном интеграле
Если функция
![]() непрерывна на
непрерывна на
![]() непрерывна вместе со своей производной
непрерывна вместе со своей производной![]() на
на![]() ,
причем
,
причем![]() ,
то
,
то
 (29)
(29)
Порядок вычисления:
ввести новую переменную с помощью подстановки вида
 или
или .
Выбор подходящей переменной см. по п.
1.4 (табл. 1), п-п. 1.7 и 1.8;
.
Выбор подходящей переменной см. по п.
1.4 (табл. 1), п-п. 1.7 и 1.8;продифференцировать введенную в п. 1 подстановку;
найти новые пределы интегрирования
 и
и с помощью формулы из п. 1;
с помощью формулы из п. 1;выразить все, что стоит под знаком интеграла, через новую переменную;
вычислить полученный интеграл. Отметим, что если при вычислении определенного интеграла методом замены переменной аккуратно выполнены п.1-4, то возвращаться к старой переменной не нужно, а можно вычислить интеграл, используя новую переменную.
Примеры
1)
 .
Подынтегральная функция непрерывна в
области интегрирования. Применим формулу
замены переменной. В табл. 1 находим
требуемую подстановку
.
Подынтегральная функция непрерывна в
области интегрирования. Применим формулу
замены переменной. В табл. 1 находим
требуемую подстановку![]() ,
новые пределы интегрирования имеют
вид: если
,
новые пределы интегрирования имеют
вид: если![]() ,
то
,
то![]() ,
если же
,
если же![]() ,
то
,
то![]() .
Выразив подынтегральное выражение,
вычислим полученный интеграл:
.
Выразив подынтегральное выражение,
вычислим полученный интеграл: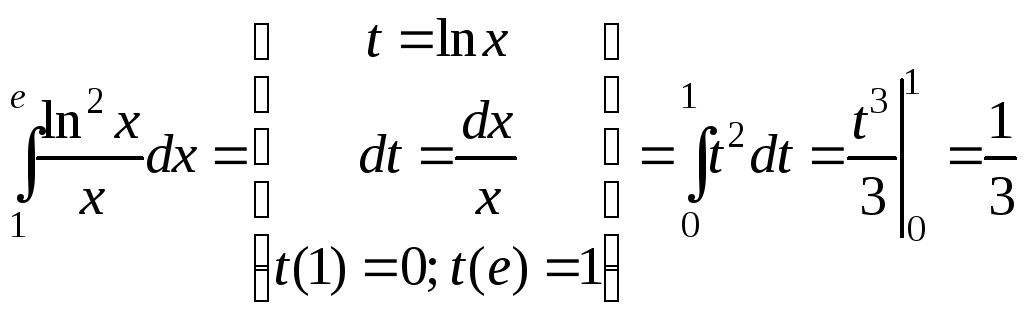 .
.
2)
 .
Подынтегральная функция – четная
относительно
.
Подынтегральная функция – четная
относительно![]() ,
поэтому по свойству 7 из п. 2.3 получим:
,
поэтому по свойству 7 из п. 2.3 получим:
 .
.
Поскольку
подынтегральная функция нечетная
относительно
![]() ,
то подстановка
,
то подстановка![]() приводит к цели (см. табл.2):
приводит к цели (см. табл.2):
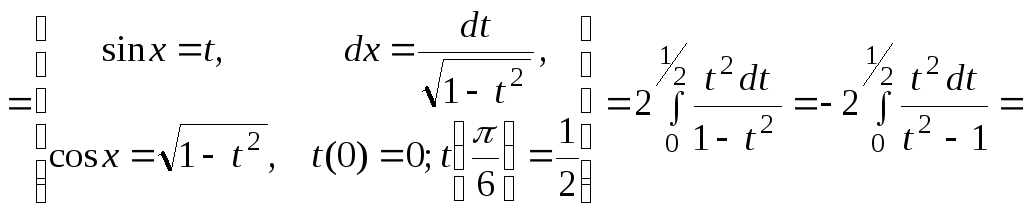

![]() .
.
3)
 .
Подынтегральная функция непрерывна в
области интегрирования. Здесь значение
интеграла можно вычислить, используя
замену
.
Подынтегральная функция непрерывна в
области интегрирования. Здесь значение
интеграла можно вычислить, используя
замену![]() :
:

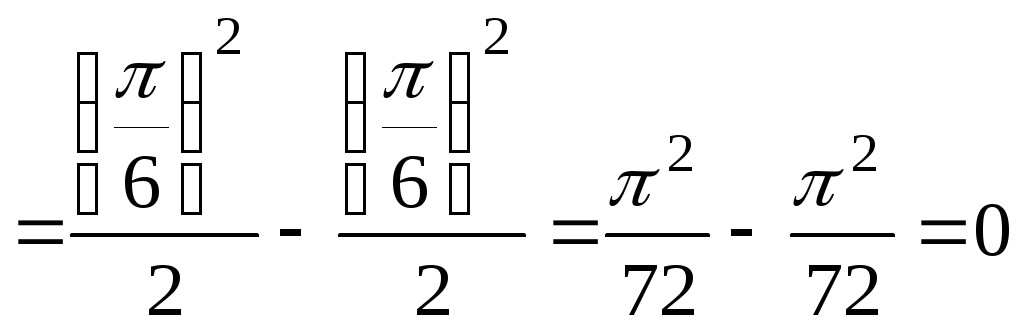 .
.
Отметим, что этот
результат можно получить и без вычислений,
заметив, что подынтегральная функция
нечетна относительно
![]() ,
и воспользовавшись свойством 8 из п.
2.3.
,
и воспользовавшись свойством 8 из п.
2.3.
2.8 Несобственные интегралы
Несобственными называются интегралы 1) с бесконечными пределами; 2) от неограниченных функций.
2.8.1. Интегралы с бесконечными пределами (несобственные интегралы I рода)
Если функция
![]() непрерывна
при
непрерывна
при
![]() ,
то по определению
,
то по определению
![]() .
(30)
.
(30)
Если этот предел существует и конечен, то несобственный интеграл называется сходящимся, если же этот предел не существует или равен бесконечности – расходящимся.
Аналогично:
![]() .
(31)
.
(31)
По определению,
если
![]() непрерывна при
непрерывна при![]() ,
то
,
то
![]() ,
(32)
,
(32)
где
![]() произвольно, причем интеграл в левой
части равенства считается сходящимся,
если сходятсяоба
интеграла
в правой части.
произвольно, причем интеграл в левой
части равенства считается сходящимся,
если сходятсяоба
интеграла
в правой части.
Порядок вычисления несобственного интеграла:
вычислить определенный интеграл с переменным пределом;
найти предел от полученного выражения.
Если
![]() непрерывна на соответствующих промежутках,
а
непрерывна на соответствующих промежутках,
а![]() - одна из первообразных, то формулы
(30)-(32) можно записать так:
- одна из первообразных, то формулы
(30)-(32) можно записать так:
![]() (33)
(33)
![]() (34)
(34)
![]() (35)
(35)
где под
![]() понимается
понимается![]() ,
а под
,
а под![]() -
-![]() .
.
Формулы (33)-(35)
аналогичны формуле Ньютона-Лейбница
(27) для интегралов с конечными пределами.
При вычислении несобственных интегралов
можно пользоваться формулой интегрирования
по частям. Можно применять и способ
подстановки, но при условии, что функция
![]() или
или![]() монотонна
на промежутке
интегрирования.
монотонна
на промежутке
интегрирования.
