
- •1.1. Задание для самостоятельной работы
- •1.2. Методические указания к выполнению аналитического расчета
- •1.3. Методические указания к выполнению моделирования
- •2. Расчет сложной цепи постоянного тока
- •2.1. Задание для самостоятельной работы
- •3. Расчет однофазной цепи переменного тока
- •3.1. Задание для самостоятельной работы
- •3.2. Методические указания к выполнению аналитического расчета
- •3.3. Методические указания к выполнению моделирования
- •4. Расчет трехфазной линейной электрической цепи
- •4.2. Методические указания к выполнению аналитического расчета
- •4.3. Методические указания к выполнению моделирования
- •5. Расчет неразветвленной неоднородной магнитной
- •5.1. Задание для самостоятельной работы
- •5.2. Методические указания к выполнению расчета
- •6. Моделирование электрических цепей с помощью программы Electronics Workbench
- •6.1. Назначение и общая характеристика программы
- •6.2. Базовые элементы цепей
- •6.3. Построение и редактирование схем
- •6.4. Запуск расчета цепи и вывод параметров. Настройка расчета
- •644046, Г. Омск, пр. Маркса, 35
4.2. Методические указания к выполнению аналитического расчета
Расчет трехфазной цепи переменного тока во всех режимах ведется символическим методом. Разберем порядок расчета на примере анализа схемы, представленной на рис. 18. Числовые значения параметров указаны в табл. 12.
Таблица 12
Числовые значения параметров элементов схемы
|
Вариант |
Напряжение, В |
Сопротивление, Ом |
Обрыв фазы |
К.з. фазы | ||||
|
R1 |
ХL1 |
R2 |
ХС2 |
ХС3 | ||||
|
– |
220 |
10 |
20 |
20 |
10 |
30 |
С |
А |



1 2 3



4 5 6



7 8 9

0
Рис. 17
4.2.1. Соединение приемников «звездой».
 Неравномерная
нагрузка с нейтральным проводом. Наличие
нейтрального провода оставляет систему
напряжений симметричной даже при
неравномерной нагрузке. Если пренебречь
сопротивлением линейных и нейтрального
проводов, то можно считать, что фазное
Неравномерная
нагрузка с нейтральным проводом. Наличие
нейтрального провода оставляет систему
напряжений симметричной даже при
неравномерной нагрузке. Если пренебречь
сопротивлением линейных и нейтрального
проводов, то можно считать, что фазное
![]() (82)
(82)
![]()
![]() (83)
(83)
![]()
![]() (84)
(84)
![]()
и линейное
-
 ;
;(85)
 ;
; ;
;(86)
 ;
; ;
;(87)

напряжение приемника и источника имеет одинаковые значения во всех фазах соответственно.
Смещение нейтрали нагрузки отсутствует.
Значения сопротивления нагрузок фаз рассчитываются по формулам:
-
 ;
;(88)

 ;
;(89)
 ;
; ;
;(90)

Фазный и линейный ток при соединении нагрузки «звездой» есть одно и то же. Значения тока определяем по закону Ома:
-
 ;
;(91)
 А;
А; ;
;(92)
 А;
А;  ;
;(93)
 А.
А.
В соответствии с первым законом Кирхгофа ток в нейтральном проводе при неравномерной нагрузке будет равен сумме токов фаз:
![]() ;
(94)
;
(94)
![]()
Нужно обратить внимание на то, что если действительная часть комплекса в алгебраической форме записи отрицательна, то при выполнении расчетов на калькуляторе необходимо к величине угла, определенного с помощью функции арктангенса, прибавить 180о для получения правильного результата.
Мощность, потребляемая цепью при соединении «звездой», может быть найдена как сумма мощностей трех фаз:
активная –
-
 ;
;(95)
 ;
; ;
;(96)
 ;
; ;
;(97)
 ;
; ;
;(98)
 ;
;
реактивная –
-
 ;
;(99)
 вар;
вар; ;
;(100)
 вар;
вар; ;
;(101)
 вар;
вар; ;
;(102)
 вар;
вар;
полная мощность –
-
 ;
;(103)
 В∙А;
В∙А;
комплекс полной мощности –
-
 ;
;(104)
 В∙А.
В∙А.
В екторная
диаграмма напряжений и токов строится
на комплексной плоскости, причем с
отличительной для трехфазных цепей
ориентацией осей (рис. 19). Выбираем
масштаб для значений напряжения и тока.
Строим равносторонний треугольник
линейных напряжений
екторная
диаграмма напряжений и токов строится
на комплексной плоскости, причем с
отличительной для трехфазных цепей
ориентацией осей (рис. 19). Выбираем
масштаб для значений напряжения и тока.
Строим равносторонний треугольник
линейных напряжений![]() ,
,![]() ,
,![]() .
Центр тяжести треугольника определяет
положение нейтральной точки источника
0, а при наличии нейтрального провода –
и приемника 0'. Векторы фазного напряжения
соединяют нейтральную точку с вершинами
А, В и С. Строим векторы фазного тока,
которые равны линейному. При построении
векторной диаграммы откладываем
направление вектора под углом, равным
величине аргумента комплексного числа,
а длину вектора – в соответствии с
выбранным масштабом, равную величине
полученного модуля. Для проверки
правильности результатов показываем
на диаграмме, что
.
Центр тяжести треугольника определяет
положение нейтральной точки источника
0, а при наличии нейтрального провода –
и приемника 0'. Векторы фазного напряжения
соединяют нейтральную точку с вершинами
А, В и С. Строим векторы фазного тока,
которые равны линейному. При построении
векторной диаграммы откладываем
направление вектора под углом, равным
величине аргумента комплексного числа,
а длину вектора – в соответствии с
выбранным масштабом, равную величине
полученного модуля. Для проверки
правильности результатов показываем
на диаграмме, что![]() (см. рис. 19).
(см. рис. 19).
Листинг расчета рассматриваемой цепи с помощью математического редактора Mathсad приведен в прил. 4.
Н
Рис. 20 еравномерная
нагрузка при обрыве линейного провода
фазы С (рис. 20): напряжение на нагрузке
оборванной фазы
еравномерная
нагрузка при обрыве линейного провода
фазы С (рис. 20): напряжение на нагрузке
оборванной фазы![]() .
Напряжение других фаз остается неизменным.
.
Напряжение других фаз остается неизменным.
![]() (105)
(105)
![]() .
(106)
.
(106)
Значения тока в фазах В и С тоже не изменились:
-
 ;
;(107)
 А;
А; ;
;(108)
 А.
А.
Ток в нейтральном проводе рассчитывается по формуле:

![]() ;
(109)
;
(109)

Векторная диаграмма напряжений и токов для неравномерной нагрузки при обрыве линейного провода фазы С представлена на рис. 21.
Обрыв нейтрального
провода при коротком замыкании фазы А
сопровождается смещением нейтрали
приемника на величину фазного напряжения.
Нейтральная точка приемника 0' совпадает
при к. з. фазы А с вершиной А треугольника
линейных напряжений, потому что
![]() ,
так как нагрузка фазы А при к. з. равна
нулю:
,
так как нагрузка фазы А при к. з. равна
нулю:![]() (рис. 22). Напряжение двух других фаз по
величине возрастает до значения линейного
напряжения, В:
(рис. 22). Напряжение двух других фаз по
величине возрастает до значения линейного
напряжения, В:

![]() (110)
(110)
![]()
![]() (111)
(111)

![]()
Токи фаз В и С можно рассчитать:
![]() (112)
(112)

![]() (113)
(113)

Ток в короткозамкнутой фазе в соответствии с первым законом Кирхгофа определяется по выражению:
![]() (114)
(114)
![]() А.
А.
Ток в короткозамкнутой фазе увеличился почти в три раза (17,06/5,7 = = 2,99). Повышенные значения напряжения и тока фаз приводят к аварии в электротехническом устройстве.
Векторная диаграмма этого режима приведена на рис. 23, листинг программы расчета с помощью Mathсad – в прил. 4.
4.2.2. Соединение
приемника «треугольником». С хема
соединения приведена на рис. 24. В качестве
приемников использованы те же
сопротивления. В соответствии со способом
соединения приемники включены между
линейными проводами и в индексах
обозначений ставятся две буквы:
хема
соединения приведена на рис. 24. В качестве
приемников использованы те же
сопротивления. В соответствии со способом
соединения приемники включены между
линейными проводами и в индексах
обозначений ставятся две буквы:
![]() (115)
(115)
![]()
![]() (116)
(116)
![]()
![]() (117)
(117)
![]()
При соединении «треугольником» линейное напряжение является одновременно и фазным как для источника, так и для приемника, если пренебречь сопротивлением соединительных проводов:
![]() В;
В;
![]() В;
(118)
В;
(118)
![]() В.
(119)
В.
(119)
Значения тока в фазах определяются по закону Ома:
-
 ;
;(120)
 А;
А; ;
;(121)
 А;
А; ;
;(122)
 А.
А.
Линейные токи находят по первому закону Кирхгофа для узлов а, в, с:
![]() (123)
(123)
![]() А;
А;
![]() (124)
(124)
![]() А;
А;
![]() ;
(125)
;
(125)
![]() А.
А.
Значения мощности, потребляемой в цепи при соединении «треугольником», определяются по выражениям:
активная –
-
 ;
;(126)
 ;
; ;
;(127)
 ;
; ;
;(128)
 ;
; ;
;
(129)
 ;
;
реактивная –
-
 ;
;(130)

 ;
;(131)
 ;
; ;
;(132)
 вар;
вар; ;
;(133)
 вар;
вар;
полная –
-
 ;
;
(134)
 ;
;
комплекс полной мощности –
-
 ;
;(135)
 В∙А.
В∙А.
Сравните полученные значения мощности при соединении нагрузки «звездой» и «треугольником» и сделайте вывод.
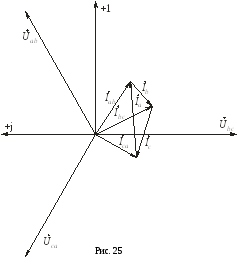
Векторная диаграмма для соединения нагрузки «треугольником» изображена на рис. 25, листинг программы расчета с помощью программы Mathсad – в прил. 4.
