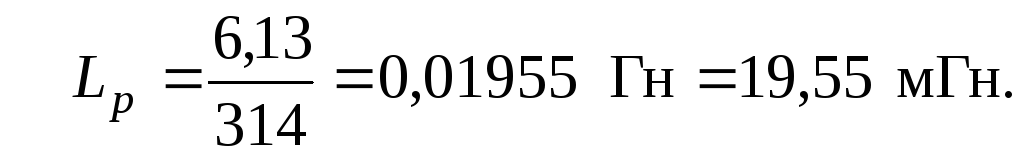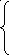- •1.1. Задание для самостоятельной работы
- •1.2. Методические указания к выполнению аналитического расчета
- •1.3. Методические указания к выполнению моделирования
- •2. Расчет сложной цепи постоянного тока
- •2.1. Задание для самостоятельной работы
- •3. Расчет однофазной цепи переменного тока
- •3.1. Задание для самостоятельной работы
- •3.2. Методические указания к выполнению аналитического расчета
- •3.3. Методические указания к выполнению моделирования
- •4. Расчет трехфазной линейной электрической цепи
- •4.2. Методические указания к выполнению аналитического расчета
- •4.3. Методические указания к выполнению моделирования
- •5. Расчет неразветвленной неоднородной магнитной
- •5.1. Задание для самостоятельной работы
- •5.2. Методические указания к выполнению расчета
- •6. Моделирование электрических цепей с помощью программы Electronics Workbench
- •6.1. Назначение и общая характеристика программы
- •6.2. Базовые элементы цепей
- •6.3. Построение и редактирование схем
- •6.4. Запуск расчета цепи и вывод параметров. Настройка расчета
- •644046, Г. Омск, пр. Маркса, 35
3. Расчет однофазной цепи переменного тока
3.1. Задание для самостоятельной работы
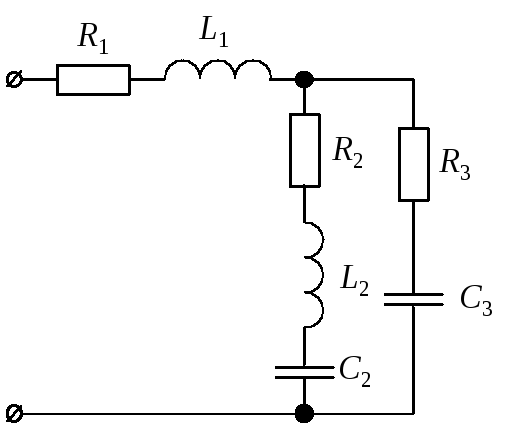
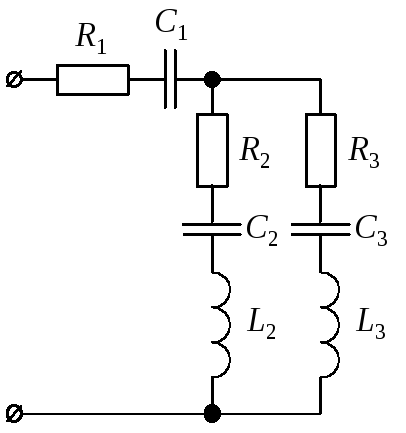
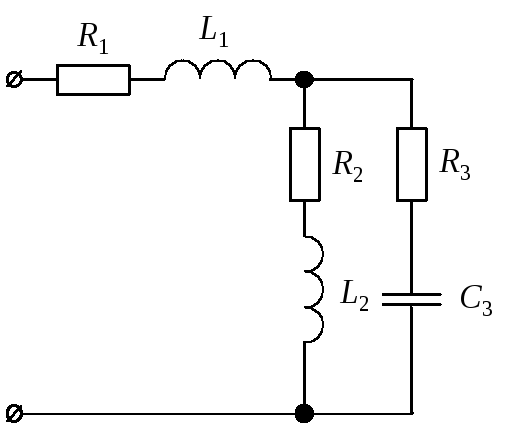
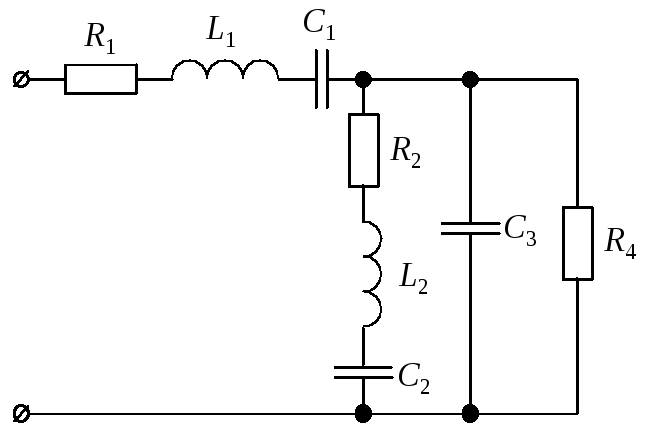
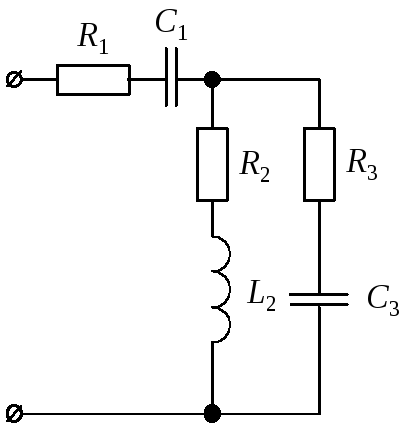
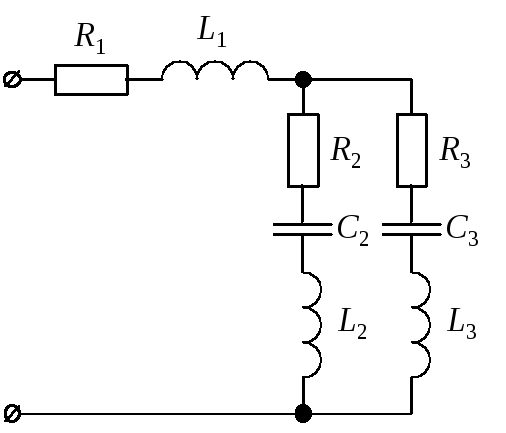
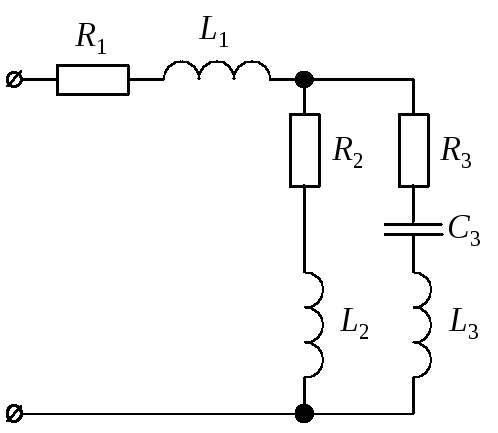
Для цепи синусоидального тока заданы параметры (табл. 8) включенных в нее элементов (рис. 10) и действующее значение напряжения на ее зажимах; частота питающего напряжения f = 50 Гц. Необходимо:
1) определить действующие значения тока в ветвях и неразветвленной части цепи символическим методом;
2) по полученным комплексным изображениям записать выражения для мгновенных значений тока в ветвях и напряжения на участке цепи с параллельным соединением;
3) построить упрощенную векторную диаграмму;
4) составить баланс мощности;
5) определить характер (индуктивность или емкость) и параметры элемента, который нужно добавить в неразветвленную часть схемы, чтобы в цепи имел место резонанс напряжений;
6) выполнить моделирование режима работы цепи при заданных параметрах и в режиме резонанса напряжений с помощью системы схемотехнического моделирования Electronics Workbench.
3.2. Методические указания к выполнению аналитического расчета
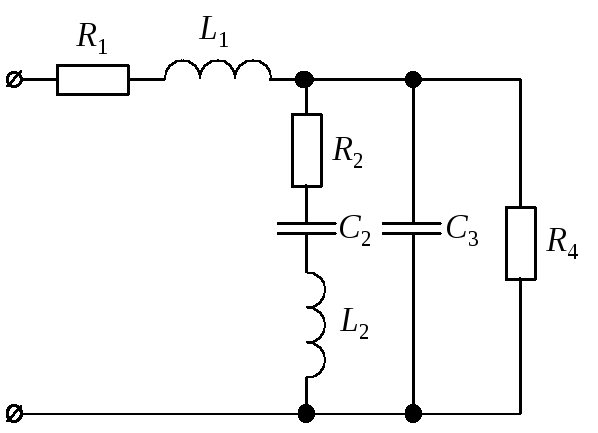
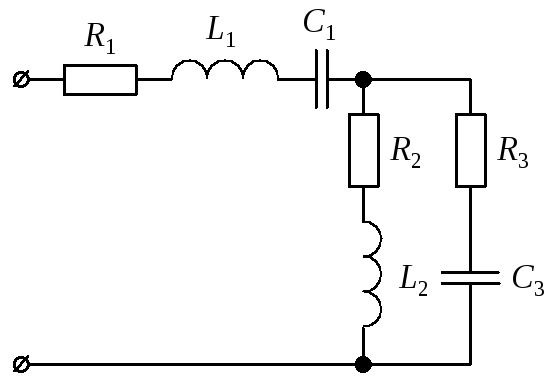
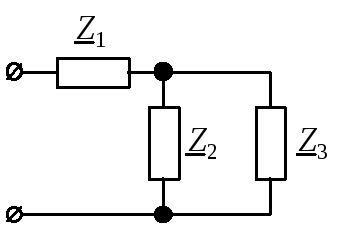
3.2.1. Рассмотрим порядок расчета однофазной цепи переменного тока на примере анализа схемы, представленной на рис. 11, а. Числовые значения параметров указаны в табл. 9.
Расчет однофазной цепи с одним источником выполняют методом эквивалентных преобразований («сворачиванием» – «разворачиванием») схемы, который рассмотрен в разд. 1.
Перед выполнением расчетов необходимо значения всех параметров привести к международной системе единиц СИ (1 мГн = 10-3 Гн; 1 мкФ = 10-6 Ф). Расчет ведется символическим методом с помощью аппарата комплексных чисел.
 1
2
1
2
3 4 5
6 7
 EMBED Word.Picture.8
EMBED Word.Picture.8
 EMBED Word.Picture.8
EMBED Word.Picture.8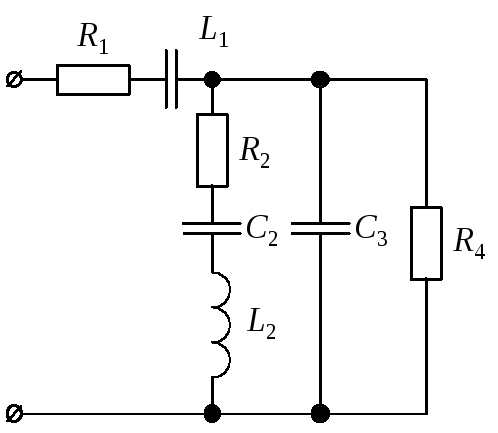
8 9 0
Рис. 10
Таблица 8
Числовые значения параметров элементов схемы
|
Вариант |
Напряжение, В |
Параметры элементов цепи | ||||||||
|
R1, Ом |
L1, мГн |
С1, мкФ |
R2, Ом |
L2, мГн |
С2, мкФ |
R3, Ом |
L3, мГн |
С3, мкФ | ||
|
0 |
220 |
9 |
15 |
800 |
9 |
17 |
1000 |
5 |
14 |
800 |
|
1 |
127 |
6 |
20 |
200 |
8 |
18 |
800 |
6 |
10 |
700 |
|
2 |
380 |
8 |
25 |
400 |
7 |
20 |
600 |
7 |
8 |
450 |
|
3 |
380 |
5 |
16 |
600 |
6 |
48 |
400 |
8 |
13 |
600 |
|
4 |
127 |
7 |
10 |
500 |
5 |
13 |
500 |
9 |
11 |
500 |
|
5 |
220 |
4 |
14 |
1000 |
12 |
31 |
700 |
10 |
9 |
400 |
|
6 |
220 |
3 |
18 |
700 |
6 |
20 |
900 |
7 |
21 |
300 |
|
7 |
127 |
6 |
12 |
300 |
7 |
16 |
450 |
8 |
18 |
200 |
|
8 |
380 |
5 |
26 |
650 |
6 |
18 |
650 |
6 |
15 |
900 |
|
9 |
127 |
8 |
24 |
480 |
8 |
26 |
800 |
4 |
12 |
600 |
Таблица 9
Числовые значения параметров элементов схемы для примера расчета
|
Вариант |
Напряжение, В |
Параметры элементов цепи | ||||
|
R1, Ом |
R2, Ом |
L2, мГн |
С2, мкФ |
С3, мкФ | ||
|
– |
127 |
5 |
10 |
20 |
200 |
300 |
Для расчета полных
комплексных сопротивлений ветвей
определим реактивные составляющие
сопротивлений (рис. 11, б), которые создают
реактивные элементы, находящиеся в
ветвях. Реактивное сопротивление
индуктивного элемента
![]() ,
емкостного –
,
емкостного –![]() ,
общее сопротивление ветви, содержащей
индуктивный и емкостный элементы, –
,
общее сопротивление ветви, содержащей
индуктивный и емкостный элементы, –![]() ,
где
,
где![]() рад; f = 50 Гц – частота питающего
напряжения.
рад; f = 50 Гц – частота питающего
напряжения.
Первая ветвь цепи
не содержит реактивного элемента,
поэтому реактивная составляющая
сопротивления ветви будет равна нулю:
![]() Ом.
Ом.
Вторая ветвь содержит два реактивных элемента. Общее реактивное сопротивление ветви равно алгебраической сумме индуктивного и емкостного сопротивлений. Знак «плюс» ставится у индуктивного сопротивления, «минус» – у емкостного:
-
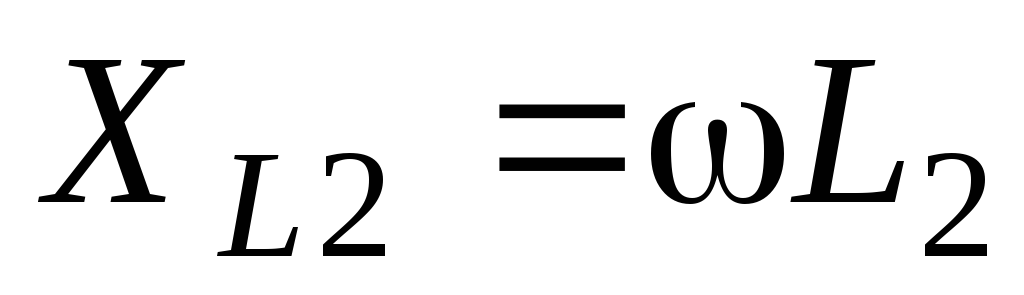 ;
;
(55)
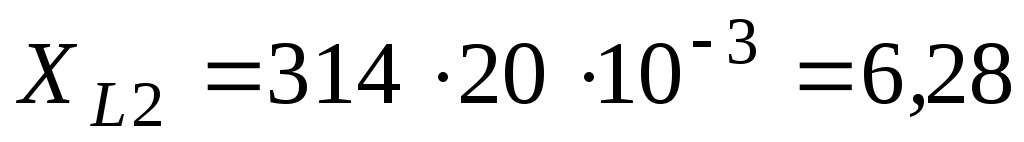 Ом;
Ом;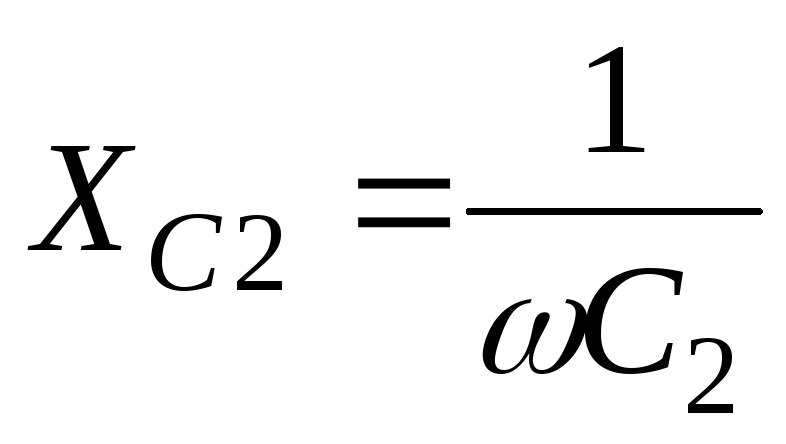 ;
; (56)
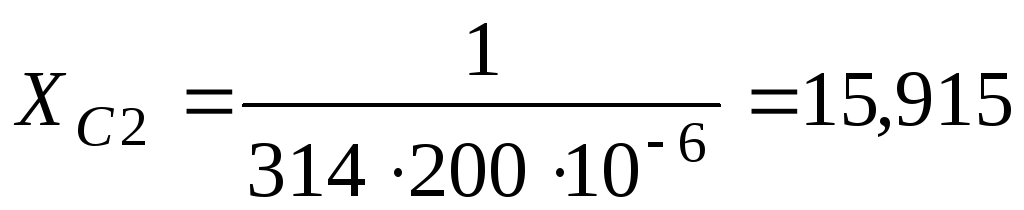 Ом;
Ом;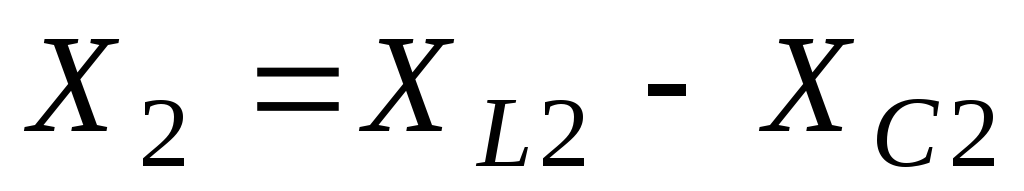 ;
;(57)
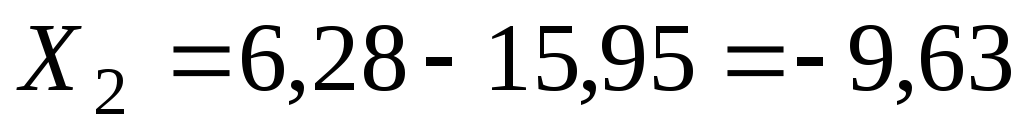 Ом.
Ом.
Знак «минус» перед общим реактивным сопротивлением ветви указывает на его емкостный характер. Этот знак сохраняется и при записи полного комплексного сопротивления (см. ниже).
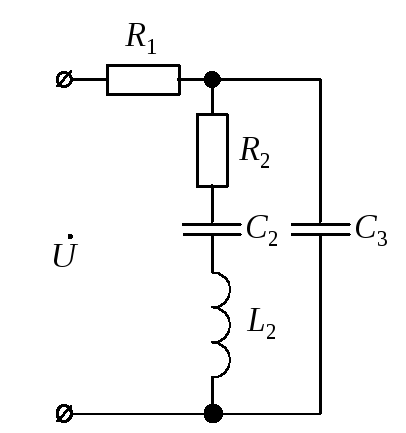
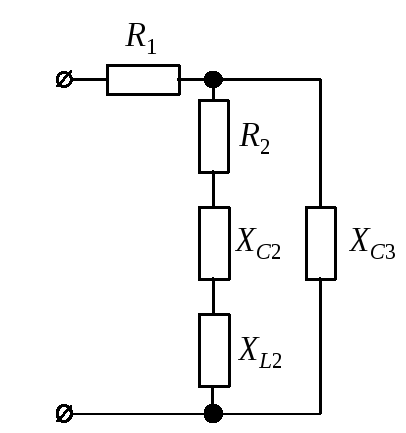
а б
в г д
Рис. 11
Реактивное сопротивление третьей ветви
-
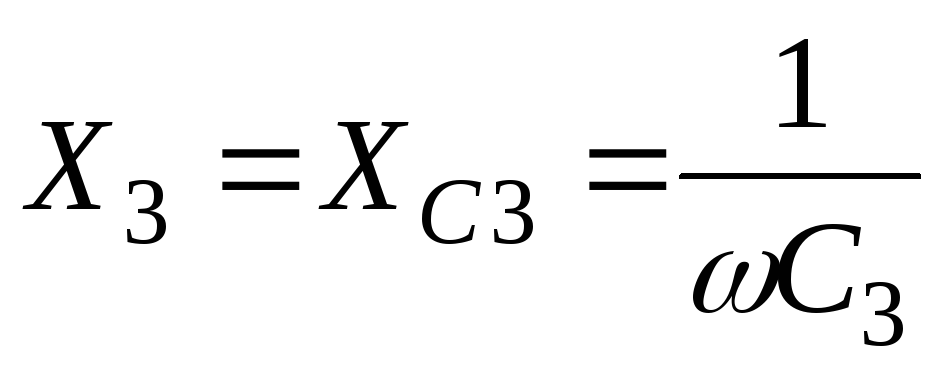 ;
;(58)
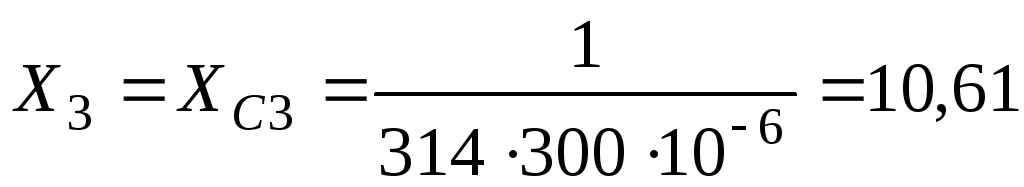 Ом.
Ом.
Полные комплексные сопротивления ветвей в алгебраической, показательной и тригонометрической форме (см. рис. 11) имеют вид:
![]() ,
(59)
,
(59)
где R – действительная составляющая комплексного сопротивления;
Х – мнимая составляющая комплексного сопротивления;
![]() –модуль комплексного
сопротивления;
–модуль комплексного
сопротивления;
![]() –аргумент
комплексного сопротивления, знак
аргумента зависит от знака реактивного
сопротивления ветви.
–аргумент
комплексного сопротивления, знак
аргумента зависит от знака реактивного
сопротивления ветви.
Для ветвей рассматриваемой электрической цепи
![]() ;
(60)
;
(60)
![]() Ом;
Ом;
![]() ;
(61)
;
(61)
![]() Ом;
Ом;
![]() ;
(62)
;
(62)
![]() Ом.
Ом.
Эквивалентная схема с учетом выполненных расчетов представлена на рис. 11, в.
Последующие операции «сворачивания» электрической схемы основаны на рассмотренных в первом разделе свойствах параллельного и последовательного соединений. Нужно помнить, что сложение и вычитание комплексных чисел выполняется в алгебраической форме записи, а умножение и сложение – в показательной, если расчеты ведутся на калькуляторе.
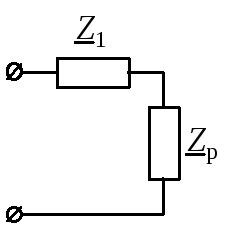
Заменим параллельный участок на эквивалентное сопротивление (рис. 11, г):
![]() ;
(63)
;
(63)
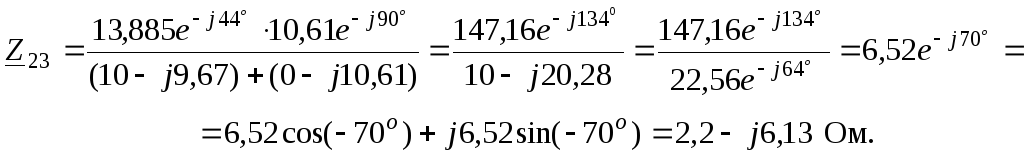
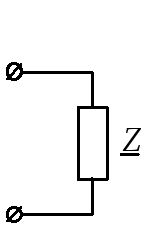
Последовательное соединение двух сопротивлений преобразуем в простейшую цепь (рис. 11, д):
![]() ;
(64)
;
(64)
![]() Ом.
Ом.
Полученная элементарная цепь рассчитывается по закону Ома для цепей переменного тока:
-
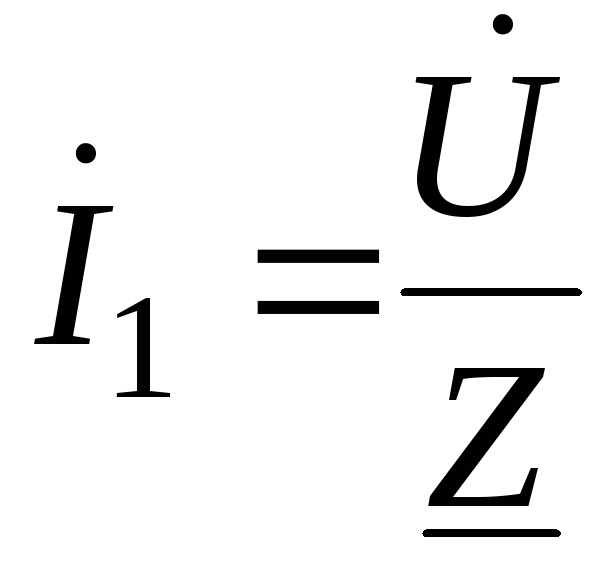 ;
; (65)
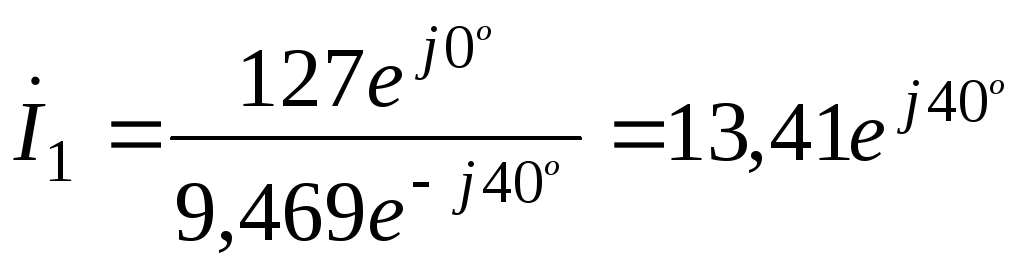
 А.
А.
Напряжение на параллельном участке
-
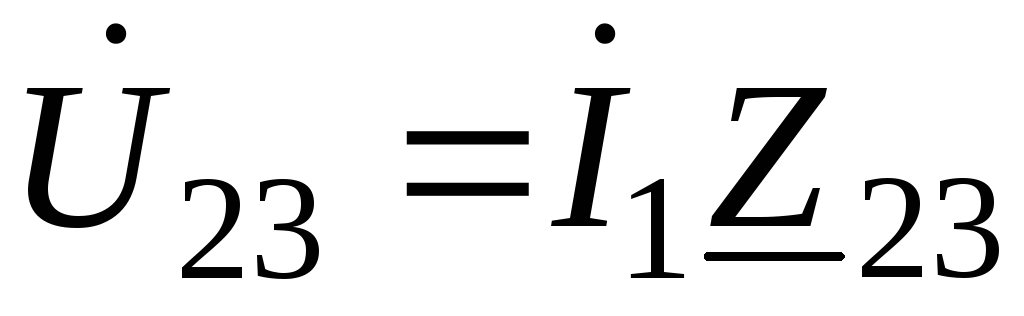 ;
;(66)
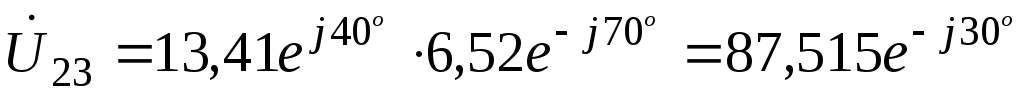 В.
В.
Токи в параллельных ветвях рассчитываются по выражениям:
-
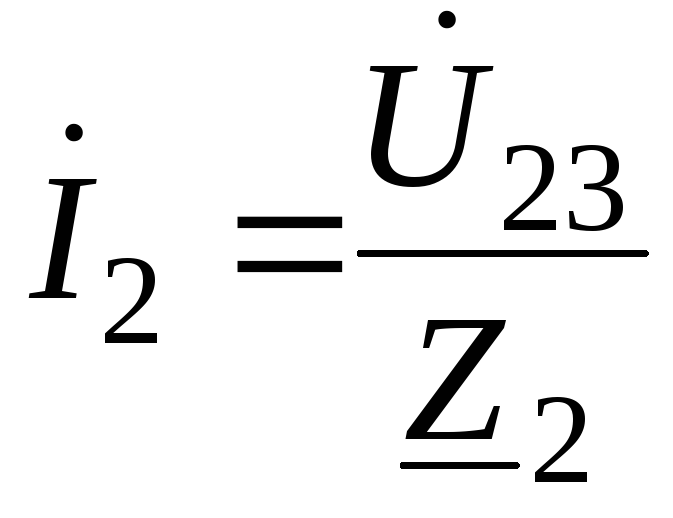 ;
;(67)
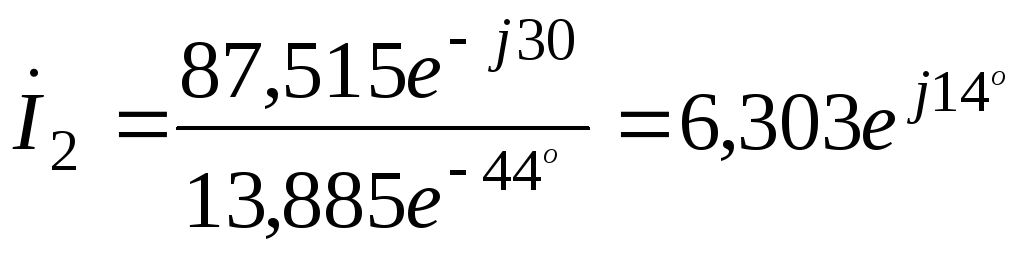 А;
А;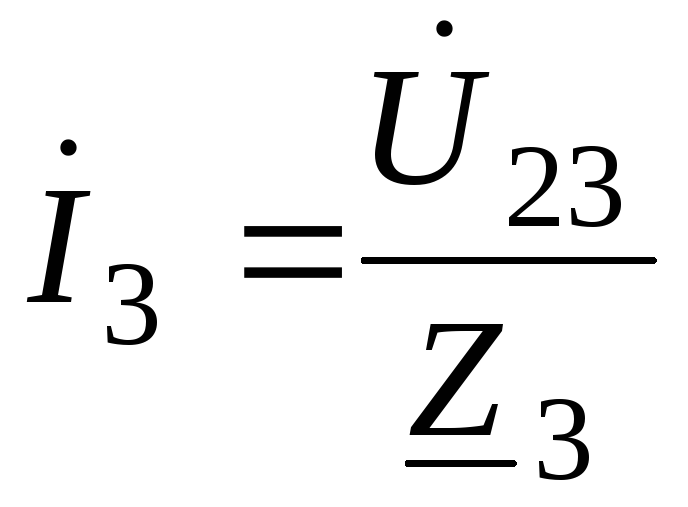 ;
;
(68)
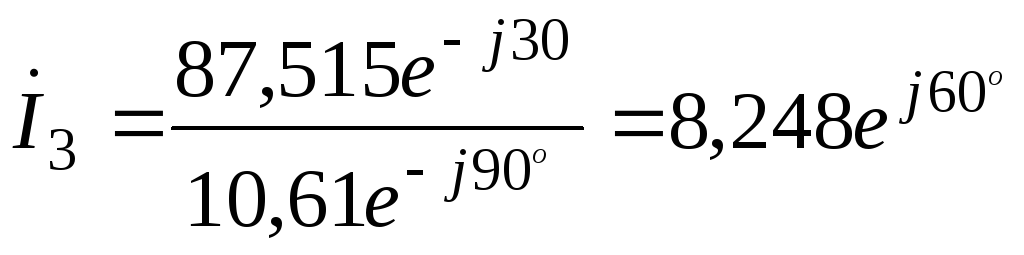 А.
А.
Для построения векторной диаграммы необходимо также определить напряжение на неразветвленной части цепи:
-
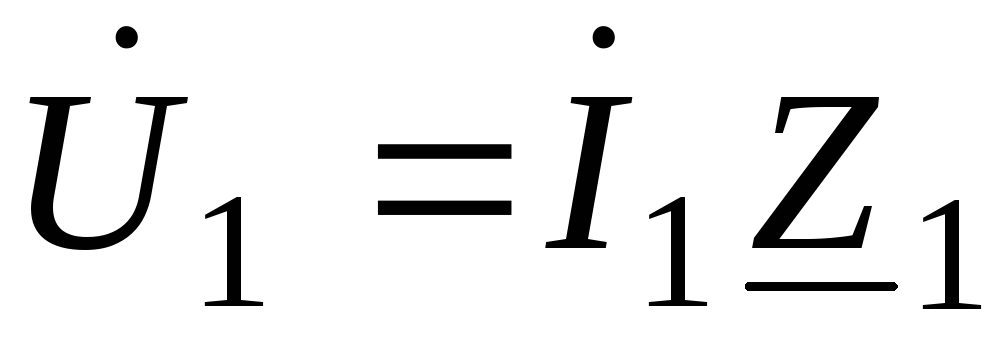 ;
;
(69)
 В.
В.
Расчет однофазной цепи с помощью математического редактора Mathсad представлен в прил. 3. Нужно заметить, что в Mathсad операции с комплексными числами выполняют в алгебраической форме записи. Для определения модулей и аргументов комплексных чисел нужно выполнить дополнительные команды. Углы в Mathсad вычисляются в радианах. Для перехода в градусную меру измерения углов необходимо дополнительно указать оператор: «deg» (см. прил. 3).
Результаты расчетов занесите в графу «Расчет» табл. 10.
Таблица 10
Полученные значения токов и напряжений для рассматриваемой цепи
|
Параметр |
Действующие значения для исходной схемы |
Моделирование резонанса | |
|
расчет |
моделирование | ||
|
I1, А |
13,44 |
13,46 |
17,57 |
|
I2, А |
6,32 |
6,352 |
8,290 |
|
I3, А |
8,26 |
8,300 |
10,83 |
|
U23, В |
87,62 |
86,96 |
113,5 |
|
φ, градус |
40,41 |
40,05 |
0 |
3.2.2. Мгновенные
значения тока в ветвях и напряжения
можно записать с учетом того, что
амплитудное значение тока в
![]() раз больше действующего значения,
которое равно модулю полученного
комплексного числа:
раз больше действующего значения,
которое равно модулю полученного
комплексного числа:
|
|
(70) |
|
|
|
(71) |
|
|
|
(72) |
|
|
|
(73) |
|
|
|
(74) |
|
3
Рис. 12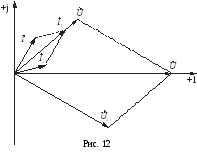
![]() ,
А/мм, и по напряжению
,
А/мм, и по напряжению![]() ,
В/мм, построить систему ортогональных
осей комплексной плоскости (+1, +j). Векторы
тока и напряжения строят из начала
координат так, чтобы длина вектора была
равна модулю комплексного числа
(действующему значению) с учетом масштаба,
а угол наклона к действительной оси
(+1) – аргументу комплексного числа
(начальной фазе), причем положительные
углы откладываются против часовой
стрелки, отрицательные – по часовой.
Векторная диаграмма для рассматриваемого
примера приведена на рис. 12.
,
В/мм, построить систему ортогональных
осей комплексной плоскости (+1, +j). Векторы
тока и напряжения строят из начала
координат так, чтобы длина вектора была
равна модулю комплексного числа
(действующему значению) с учетом масштаба,
а угол наклона к действительной оси
(+1) – аргументу комплексного числа
(начальной фазе), причем положительные
углы откладываются против часовой
стрелки, отрицательные – по часовой.
Векторная диаграмма для рассматриваемого
примера приведена на рис. 12.
Если на векторной диаграмме сумма векторов токов параллельных ветвей равна вектору тока в неразветвленной части цепи в соответствии с первым законом Кирхгофа для узловой точки, а сумма векторов напряжения – напряжению источника, то считается, что диаграмма сходится, и это обязательное, но не достаточное условие для вывода о правильности расчетов.
3.2.4. Окончательно о правильности полученных результатов можно судить по балансу мощности, который для цепей переменного тока может быть составлен для комплексов полной мощности источника и потребителей:
![]() ,
(75)
,
(75)
или для активной и реактивной мощностей как составляющих. Выполним проверку по балансу активной и реактивной мощностей:
|
|
(76) |
где
![]() ,
,![]() – угол сдвига фаз между приложенным
напряжением и током в неразветвленной
части цепи, он зависит от нагрузки цепи
и равен аргументу полного комплексного
сопротивления
– угол сдвига фаз между приложенным
напряжением и током в неразветвленной
части цепи, он зависит от нагрузки цепи
и равен аргументу полного комплексного
сопротивления![]() ;
;
![]() ;
;
![]() ,
где
,
где
![]() – действующие значения токов, т. е.
модули комплексных чисел, изображающих
соответствующие токи;
– действующие значения токов, т. е.
модули комплексных чисел, изображающих
соответствующие токи;
![]() ,
реактивное сопротивление берется с
учетом знака.
,
реактивное сопротивление берется с
учетом знака.
Активная мощность всегда положительна, реактивная может быть и отрицательной. Знак «минус» указывает на то, что реактивная мощность отдается цепью в сеть, а не потребляется из сети.
Для рассматриваемого примера:
![]() Вт;
Вт;
![]() Вт;
Вт;
![]() вар;
вар;
![]()
В результате баланс активной мощности:
1297 Вт = 1297 Вт,
а реактивной:
– 1105 вар = – 1105 вар.
Баланс активной и реактивной мощности выполняется, следовательно, расчет однофазной цепи выполнен верно.
3.2.5. Резонанс
напряжений в цепи наступает тогда, когда
реактивное сопротивление цепи равно
нулю. Если реактивное сопротивление
цепи носит индуктивный характер (![]() ),
то необходимо в неразветвленную часть
цепи добавить емкостное сопротивление,
значение которого равно индуктивной
составляющей сопротивления:
),
то необходимо в неразветвленную часть
цепи добавить емкостное сопротивление,
значение которого равно индуктивной
составляющей сопротивления:
![]() (77)
(77)
![]() .
(78)
.
(78)
Если реактивное
сопротивление цепи носит емкостный
характер (![]() ),
то необходимо в неразветвленную часть
цепи добавить индуктивное сопротивление:
),
то необходимо в неразветвленную часть
цепи добавить индуктивное сопротивление:
![]() (79)
(79)
![]() .
(80)
.
(80)
В рассматриваемом
примере
![]() ;
реактивная составляющая сопротивления
– емкостная. Рассчитаем индуктивное
сопротивление, которое обеспечит в цепи
резонанс напряжений:
;
реактивная составляющая сопротивления
– емкостная. Рассчитаем индуктивное
сопротивление, которое обеспечит в цепи
резонанс напряжений:
-
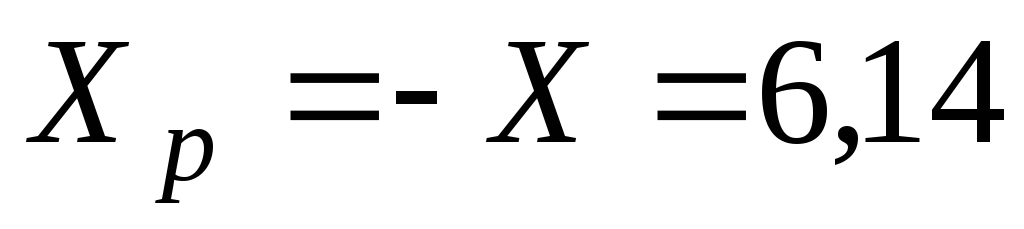 Ом;
Ом;