§ 9. Основные законы распределения.

Биномиальный закон. Случайная величина называется распределенной побиномиальному закону, если она принимает конечное множество значений 0,1,…, а вероятность того, что, выражается формулой:, где- вероятность наступления событияА при одном испытании, .

Числовые характеристики биномиального закона распределения: ,.

Закон Пуассона. Дискретная случайная величина называется распределенной позакону Пуассона, если она принимает счетное множество значений 0, 1, 2, …, , …, а вероятность того, что, выражается формулой:, где– параметр закона Пуассона. Числовые характеристики закона Пуассона:,.Опр. Интенсивностью потока наз-ют среднее число событий, которые появляются в единицу времени. Док-но, что если известна постоянная интенсивность потока, то вер-ть появлениясобытий за время длительностьюопределяется форм.:.

Равномерное распределение.Непрерывная случайная величина называется равномерно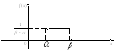распределенной в интервале , если ее плотность распределения в этом интервале постоянна, а вне его равна нулю: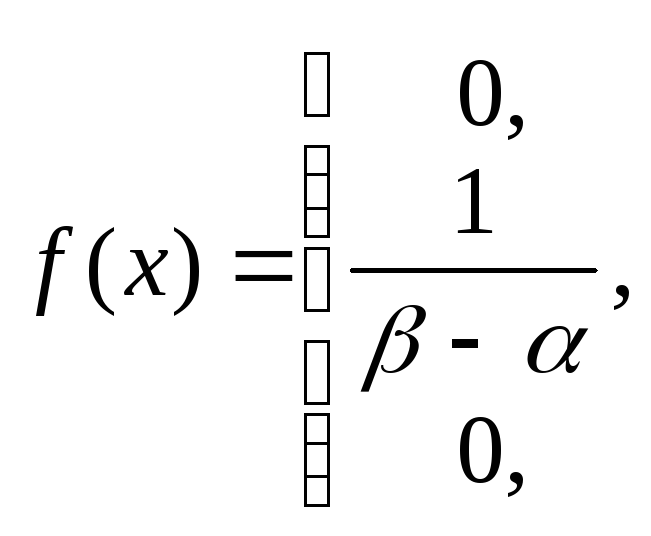 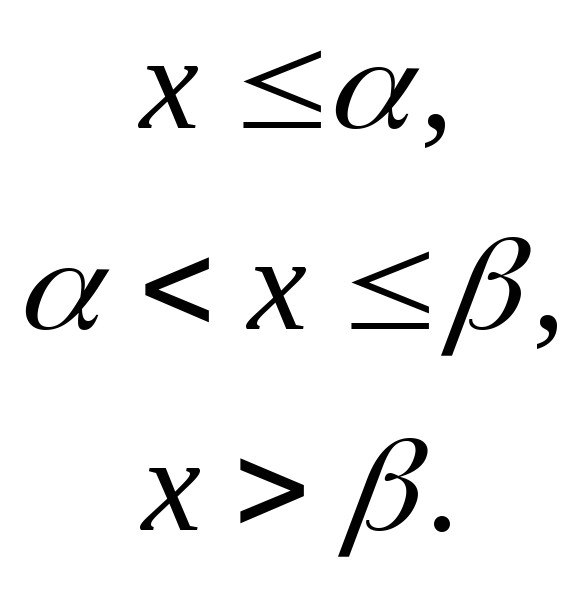Числовые характеристики равномерного закона распределения:,.

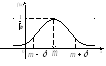
График дифференциальной функции равномерного распределения приведен на рис.

Нормальное распределение. Непрерывная случайная величина называется нормально распределенной, если ее плотность распределения равна , где- математическое ожидание,- среднее квадратическое отклонение. График дифференциальной ф-иинормального закона распределения (нормальная кривая или кривая Гаусса) на рис.

Вероятность того, что нормально распределенная случайная величина примет значение в интервале, выражается формулой:, где. Для нормального закона распределения верна следующая формула:.

Показательное распределение. Показательным называется распределение, дифференциальная функция которого имеет вид 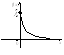где – параметр показательного распределения. График дифференциальной функции показательного распределения приведен на рис. Числовые характеристики показательного распределения:,. Интегральная функция для показательного распределения имеет вид.Функция надежности. Показательное расп-е широко применяется в теории надежности. Пусть – продолжительность безотказной работы прибора. Ф-я распределения случайной величиныТ выражает вероятность отказа за время t: . Опр. Функцией надежности наз-ют ф-ю, определяющую вероятность безотказной работы элемента за время длительностью :. Для показат. закона рас-я вер-ть безотказ. работы элемента за времявыч-ся по формуле:, где- интенсивность отказов.

§ 10. Элементы математической статистики

Математическая статистика занимается разработкой методов получения, описания и обработки опытных данных с целью получения закономерностей случайных массовых явлений.

Задачи математической статистики: Первая задача – указать способы сбора и группировки статистических данных. Вторая задача – разработать методы анализа и обработки полученных статистических данных в зависимости от целей исследований.

Опр. Совок-сть N объектов, из которых производится выборка объектов для исследования, называется генеральной совокупностью.

Опр. Сов-ть п объектов, случайно отобранных из генеральной сов-ти, наз-ся выборочной совокупностью или выборкой ().

Опр. Выборка наз-ся бесповторной, если отобранный для ис-я случайным образом объект в ген-ую совокупность не возвращается.

Опр. Выборка наз-ся повторной, если отобран. случ. образом объект перед отбором след-го объекта возвращается в ген-ую сов-ть.

Для того, чтобы выборка давала правильное представление о генеральной совокупности, она должна быть представительной или репрезентативной, т.е. для каждого объекта генеральной совокупности вероятность попасть в выборку одна и та же.

Пусть совокупность объектов исследуется по некоторому признакуХ. Произведем выборку объема п. Пусть в результате эксперимента случайная величина Х приняла значения раз,раз, … ,раз, причем

Опр. Наблюдаемые значения называетсявариантами, а последовательность вариант, записанных в возрастающем порядке, называется вариационным рядом. Опр. Числа называется частотами, числа наз-сяотносительными частотами,

Опр. Статистическим распределением выборки наз-ся задание вариант и соответствующих им частот или относительных частот.

Опр. Таблица

… …

или

… …

называется статистическим рядом. Пусть изучается генеральная совокупность относительно некоторого признака Х. – возможные значения этого признака, причем все различные.

Опр. Генеральной средней называется среднее арифметическое возможного значения

Если же не все значения различны, а различные значения признакаХ принимаются раз,раз, … ,раз, тогда. Пред-им, что все объекты генер-ой сов-ти объемаимеют различные значения. Если взять один объект, то вероятность, что он обладаетпризнаком, равна. Тогда. Итак, генеральная средняя есть математическое ожидание рассматриваемого признакаХ.

Пусть требуется изучить генеральную совокупность объема относительно признакаХ. Извлечем выборку объема п.

Опр. Выборочной средней называется среднее арифметическое значений признака выборочной совокупности. Если не все значения признака различны, то.

Если из генеральной сов-ти извлечена выборка, то она имеет выборочную среднюю, которая является определенным числом. Другая выборка, извлеченная из генеральной совокупности, будет иметь свою выборочную среднюю, которую можно рассматривать как случайную величину, а следовательно, можно говорить о распределении выборочной средней и о ее числовых характеристиках.

Зам. В теоретических рассуждениях выборочные значения признака Х рассматриваются как случайные величины, имеющие то же распределение и те же числовые характеристики, что и признак Х.

Рассмотрим генеральную совокупность объема . Пусть- значения количественного признакаХ – различны.

Опр. Генеральной дисперсией наз-ся среднее арифметическое квадратов отклонений значений признакаген-ой сов-ти от ген-ой средней.. Если же не все значения признака различны, т.е.раз,раз, … ,раз, то. Средним квадратическим отклонением генеральной сов-ти наз-ся

Пусть требуется изучить генеральную совокупность объема относительно признакаХ. Извлечем выборку объема п.

Опр. Выборочной дисперсией наз-ся среднее арифметическое квадратов отклонений значений признакавыборочной сов-ти от выборочной средней.. Если же не все значения признака различны, то. Средним квадратическим отклонением выборочной совокупности называется

Пусть известно статистическое распределение некоторого признака Х. х – некоторое действительное число. Обозначим - сумму частот, варианты которых меньшех. Тогда – относительная частота события

Опр. Статистической (эмпирической) фун-ей распределения наз-ся функция . Статистическая ф-ясходственна с интегральной ф-ей распределения, которую в матем. статистике наз-юттеоретической фун-ей распред-я.

Различие между этими ф-ми состоит в том, что задает вероятность события,задает относительную частоту этого события Фун-я обладает всеми св-ми ф-и: 1).2)– неубывающая ф-я.3) Еслито=0, еслито=1. В целях наглядности строят графики статистического распред-я выборки.

Опр. Полигоном частот называется ломаная линия с вершинами в точках . Полигоном относительных частот называется ломаная линия с вершинами в точках.

Опр. Гистограммой частот (относительных частот) называется ступенчатая фигура, состоящая из прямоугольников, основаниям которых служат отрезки длины , лежащие на осиОх, а высотами –отрезки длиной . Значения длинвыбираются следующим образом. Интервал, на котором находятся все значения вариант, делят нат равных частей и через обозначают сумму всех частот, варианты которых оказались на-ом отрезке. Если в генеральной совокупности признак имеет дискретное значение, то промежуток в котором находятся варианты разбиваем на части так, чтобы на каждом участке была одна варианта.