
- •Часть 1
- •Часть 1
- •1.1. Теоретические сведения
- •1.1.1. Области Mathcad-документа
- •1.1.2. Определение переменных
- •1.1.3. Ввод и редактирование формул
- •Получим результат:
- •1.2. Пример выполнения работы Лабораторная работа 1
- •1.3. Задания
- •Цель работы: изучение приемов работы в системеMathcadпри табуляции значений и построении графиков функций.
- •2.1. Теоретические сведения
- •2.1.1 Определение переменных, получающих значения из заданного диапазона
- •2.1.3. Пример построения графика
- •2.2. Пример выполнения работы Лабораторная работа 2
- •2.3. Задания
- •3.1. Теоретические сведения
- •3.1.1. Условный оператор
- •3.1.2. Операторы циклов for и while
- •Пример 1. Вычислить сумму значений Решение:
- •Пример 2. Вычислить сумму значений Решение:
- •3.1.3. Оператор прерываний break
- •Пример выполнения работы Лабораторная работа 3
- •Задания
- •4.1. Теоретические сведения
- •4.1.1. Метод половинного деления
- •4.1.2. Метод Ньютона
- •4.1.3. Метод простой итерации
- •4.1.4. Встроенные функции Mathcad для поиска корней уравнений
- •Пример выполнения работы
- •5.1. Теоретические сведения
- •5.1.1. Действия над матрицами
- •Поэлементное умножение матриц с использованием векторизации
- •5.1.2. Решение матричных уравнений
- •5.2. Пример выполнения работы Лабораторная работа 5
- •Задания
- •Часть 1
- •644046, Г. Омск, пр. Маркса, 35
4.1.1. Метод половинного деления
Для
нахождения корня уравнения y
= f(x),
принадлежащего отрезку [a, b], делим
этот отрезок пополам. Если
 то
то![]() является корнем уравнения. Если
является корнем уравнения. Если (что, практически, наиболее вероятно),
то выбираем ту часть отрезка
(что, практически, наиболее вероятно),
то выбираем ту часть отрезка или
или ,
на концах которого функцияf(x)
имеет
противоположные знаки. Процесс деления
отрезка продолжается до тех пор, пока
длина отрезка больше заданной точности
вычислений.
,
на концах которого функцияf(x)
имеет
противоположные знаки. Процесс деления
отрезка продолжается до тех пор, пока
длина отрезка больше заданной точности
вычислений.
Метод половинного деления метод прост и надежен, удобен для практического применения. Алгоритм, реализующий метод половинного деления, представлен на рис. 13.
4.1.2. Метод Ньютона
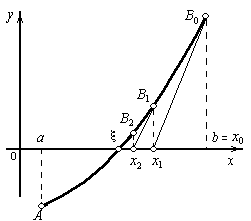
Сущность данного метода заключается в том, что на первом шаге вычислений из точки начального приближения х0 восстанавливается перпендикуляр до пересечения с графиком функции f(x). Из точки пересечения проводится касательная к графику y = f(x). Точка пересечения касательной с осью абсцисс служит точкой следующего приближения (рис. 14). Для инициализации вычислительного процесса достаточно задать некоторое начальное приближение корня x = х0.

Рис. 13. Графическая схема алгоритма метода половинного деления
Применяя метод Ньютона, следует руководствоваться следующим правилом: в качестве исходной точки х0 выбирается тот из концов отрезка [а, b], для которого справедливо условие: f(х0)∙f (х0) > 0. Это условие сходимости метода Ньютона.
Уравнение касательной, проведенной к графику y = f(x) через точку В0 с координатами х0 и f(х0), имеет вид:
![]() .
(1)
.
(1)
Отсюда найдем следующее приближение корня х1 как абсциссу точки пересечения касательной с осью Ох (y = 0):
 (2)
(2)

Рисунок 1. Метод Ньютона
Запишем формулу (2) в общем виде:
 .
(3)
.
(3)
Формула (3) итерационная формула рекуррентного процесса.
Алгоритм, реализующий метод Ньютона, представлен на рис. 15.
4.1.3. Метод простой итерации
Для использования метода итерации1 исходное нелинейное уравнение f(х) = 0 заменяется равносильным:
x = (x). (4)
Пусть известно начальное приближение корня х = х0. Подставляя это значение в правую часть уравнения (4), получим новое приближение:
х1 = (х0). (5)

Рис. 15. Графическая схема алгоритма метода Ньютона
Подстановка нового значения корня в уравнение (4) дает возможность получить последовательность значений:
![]() (6)
(6)
Процесс сходимости метода итераций по «лестнице» представлен на рис. 16, а, по «спирали» на рис. 16, б.
Построим
на плоскости хОу графики функций у = х
и у = (х).
Каждый действительный корень
![]() уравнения (4) является абсциссой точки
пересечения М кривой у = (х)
с прямой у = х (см. рис. 16, а).
уравнения (4) является абсциссой точки
пересечения М кривой у = (х)
с прямой у = х (см. рис. 16, а).

Рис. 16. Геометрическая интерпретация метода итераций
От
некоторой точки А0
[x0,
(x0)]
строим ломаную линию А0В1А1В2А2...
(«лестница»), звенья которой попеременно
параллельны осям Ох и Оу. Вершины А0,
А1,
А2, ...
лежат на кривой у =
(х), а В1,
В2,
В3
…
на прямой у = х. Общие абсциссы точек А1
и В1,
А2
и В2,
… представляют собой соответственно
последовательные приближения х1,
х2,
… корня
![]() .
.
Возможен также другой вид ломаной А0В1А1В2А2 ... – «спираль» (см. рис. 16, б).
Решение в виде «лестницы» получается, если производная (х) положительна, а в виде «спирали», если (х) отрицательна.
Алгоритм, реализующий метод итераций, представлен на рис. 17.
