- •Р. С. Курманов, л. А. Литневский
- •Векторы
- •Производные и интегралы
- •Движение с постоянным ускорением
- •Движение с переменным ускорением Рассматривая формулу определения ускорения в общем случае
- •Аналогично, рассматривая формулу определения скорости в общем случае
- •Движение тел под действием постоянных сил
- •Движение тел под действием переменной силы
- •Библиографический список
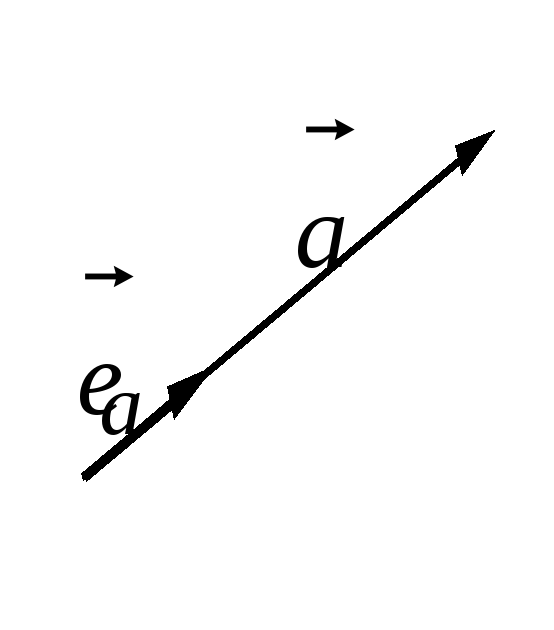
- •Проекция вектора на ось При работе с векторами удобно придерживаться следующих обозначений:– вектор (в учебниках обозначается жирной буквой без стрелочки);
- •Обратите внимание: проекции вектора на разные оси могут быть разными, а модуль вектора не зависит от выбора осей.
- •Действия над векторами
- •Правила дифференцирования и таблица производных
- •Правила интегрирования и таблица интегралов
- •Справочные сведения
- •Литневский Леонид Аркадьевич
Библиографический список
1. Трофимова Т. И. Курс физики / Т. И. Трофимова. М., 1997. 542 с.
2. Детлаф А. А. Курс физики / А. А. Детлаф, Б. М. Яворский. М., 2000. 718 с.
3. Савельев И. В. Курс общей физики / И. В. Савельев. М., 1989. Т. 1. 352 с.
ПРИЛОЖЕНИЕ 1
Проекция вектора на ось При работе с векторами удобно придерживаться следующих обозначений:– вектор (в учебниках обозначается жирной буквой без стрелочки);
a,
![]() – модуль вектора (длина вектора, числовое
значение вектора);
– модуль вектора (длина вектора, числовое
значение вектора);
![]() –проекция
вектора
–проекция
вектора ![]() на ось Ох
(компонента вектора);
на ось Ох
(компонента вектора);
![]() –составляющая
вектора
–составляющая
вектора ![]() по оси Ох.
по оси Ох.
|
Рис. П.1.1 |
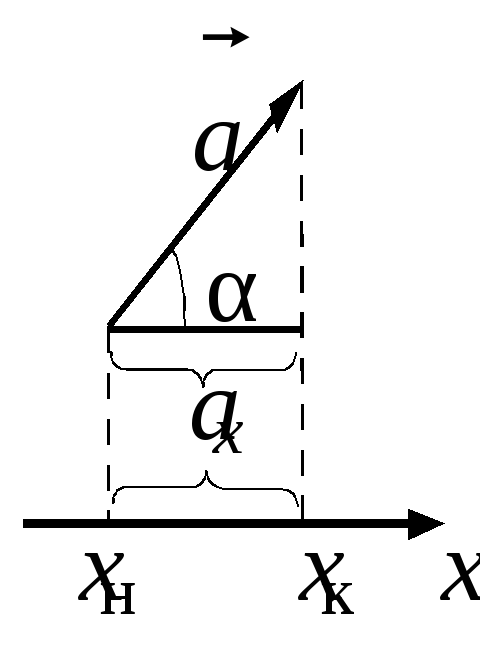
Проекцией
вектора
где a – модуль вектора; α – угол между вектором и осью (рис. П.1.1). Составляющая
|
Пример. Пусть в некоторый момент времени угол между вектором ско-рости тела и осью Ох равен 30о, а длина вектора скорости равна 2,8 м/с. Найти проекции вектора скорости на координатные оси Ох и Оу.
|
Рис. П.1.2 |
Дано: v vx, vy – ? Решение: vx = v cos α1; vx = 2,8 cos 30о = 2,4 (м/с); vy = v cos α2; vy = 2,8 cos (90о + 30о) = – 1,4 (м/с). |
Обратите внимание: проекции вектора на разные оси могут быть разными, а модуль вектора не зависит от выбора осей.
Таблица П.1.1
Пять частных случаев вычисления проекции
|
Проекция вектора равна модулю. |
|
Проекция вектора равна нулю. |
|
Проекция вектора равна «минус модуль». |
|
Проекция вектора положительна. |
|
Проекция вектора отрицательна. |
Обратите внимание: если составляющая вектора направлена в ту же сторону, что и ось, то проекция такого вектора положительна; если составляющая направлена против оси, то проекция вектора отрицательна.
ПРИЛОЖЕНИЕ 2
Действия над векторами
|
|
Сложение векторов:
выполняется по правилу треугольника или параллелограмма. При
сложении векторов по правилу треугольника
(рис. П.2.1) длина результирующего вектора
При сложении векторов по правилу параллелограмма (рис. П.2.2) из теоремы косинусов легко получить выражение для вычисления длины результирующего вектора:
Умножение вектора на число (рис. П.2.3) изменяет только длину вектора, если число положительное, а при отрицательном числе изменяет еще и нап-равление вектора на противоположное:
|
Вычитание
векторов
с учетом действия (П.2.4) сводится к
сложению вектора
![]() с вектором, противоположным вектору
с вектором, противоположным вектору![]() :
:
![]() .
.
Скалярное произведение векторов определяется выражением:
![]() ,
,
где
α – угол между векторами
![]() и
и![]() .
.
Векторное произведение векторов можно записать так:
![]() ,
,
|
где
Рассмотрим характеристикивектора. Используя
правило умножения вектора на число,
произвольный вектор
где
a
– длина (модуль);
Проекция вектора на ось (рис. П.2.6) определяется формулой:
где α – угол между вектором и осью x (0 ≤ α ≤ π). |
Рис. П.2.4
Рис. П.2.5
Рис. П.2.6 |
Вектор
можно разложить
по трем взаимно перпендикулярным
направлениям
в пространстве, например по трем
декартовым осям координат. Выбрав
единичные векторы (орты)
![]() (иногда обозначаются как
(иногда обозначаются как![]() )
вдоль осейOx,
Oy
и Oz,
любой вектор можно представить в виде:
)
вдоль осейOx,
Oy
и Oz,
любой вектор можно представить в виде:
![]() ,
,
где
![]() –
проекции вектора
–
проекции вектора
![]() на
оси декартовой системы координат.
на
оси декартовой системы координат.
Тогда модуль вектора рассчитывается по формуле:
![]() .
.
Формула позволяет выполнять действия над векторами аналитически, без геометрического сложения на рисунке, что особенно удобно в том случае, если векторы изменяются с течением времени.
ПРИЛОЖЕНИЕ 3




 = 2,8 м/с, α1
= 30о.
= 2,8 м/с, α1
= 30о.




 Рис.
П.2.1
Рис.
П.2.1 Рис.
П.2.2
Рис.
П.2.2 Рис.
П.2.3
Рис.
П.2.3