
- •2350Министерство транспорта Российской Федерации
- •Инженерная геодезия
- •2.1. Способ прямоугольных координат
- •2.2. Способ условных прямоугольных координат
- •2.3. Способ прямой угловой засечки
- •2.4. Способ полярных координат
- •2.5. Способы детальной разбивки сооружений
- •5.1. Метод координат
- •5.2. Метод хорд
- •5.3. Метод углов
- •5.4. Метод продолженных хорд
- •Контрольные вопросы
- •Библиографический список
2350Министерство транспорта Российской Федерации
Федеральное агентство железнодорожного транспорта
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
САМАРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ
Кафедра «Путь и строительство железных дорог»
Инженерная геодезия
Методические указания к выполнению практических работ
для студентов специальности 270204
«Строительство железных дорог, путь и путевое хозяйство»
очной и заочной форм обучения
Составители: А.Д. Громов
В. Г. Рахчеев
Самара
УДК 528.656.21
Инженерная геодезия : методические указания к выполнению практических работ для студентов специальности 270204 «Строительство железных дорог, путь и путевое хозяйство» очной и заочной форм обучения [текст] / составители : А.Д. Громов, В.Г. Рахчеев. – Самара : СамГУПС, 2009. – 28 с.
Утверждены на заседании кафедры 7 мая 2009 г., протокол № 9.
Печатаются по решению редакционно-издательского совета университета.
Приведены практические работы, предусмотренные новой программой дисциплины «Инженерная геодезия». Выполнение данного цикла практических работ позволит студентам получить более полные и органичные знания по изучаемому курсу, полноценно воспринимать полученный материал, принимать грамотные инженерные решения в ходе выполнения курсовых и дипломных проектов по дисциплинам строительного цикла. Практические работы выполняются в учебной аудитории и на учебном полигоне СамГУПС на ул. Литвинова, 332 А.
Составители: Александр Дмитриевич Громов
Валерий Геннадьевич Рахчеев
Рецензенты:
Редактор И.М. Егорова
Компьютерная верстка Е.А. Самсонова
Подписано в печать 04.06.2009. Формат 60×90 1/16.
Усл. печ. л. 1,75. Тираж 150 экз. Заказ № 110.
Практические работы по инженерной геодезии предназначены для приобретения практических навыков в проведении съемки рельефа на открытой местности, выноса в натуру элементов инженерных сооружений, расчета элементов кривой и переноса главной точки с аэроснимка на карту.
Практическая работа № 1. Способ нивелирования по квадратам
Способ нивелирования по квадратам применяется в основном при съемке рельефа на сравнительно небольшой открытой местности со слабовыраженным рельефом (с небольшими перепадами между наиболее высокой и наиболее низкой отметками).
Плановую сеть строят в виде квадратов, а высоты точек определяют геометрическим нивелированием. Работы начинают с построения на местности сетки квадратов, которую разбивают теодолитом и мерной лентой или тросом с метками. Если нивелируемая площадь имеет значительные размеры, сначала размечают вершины больших квадратов со сторонами 100 – 1000 м. Затем каждый большой квадрат заполняют квадратами со стороной 20 – 200 м и т. д. так, чтобы длина сторон на плане не превышала 2 – 4 см.
Если территория небольшая, то сначала строят наружный полигон. Вершины квадратов закрепляют кольями, забитыми вровень с землей и сторожками, на которых отмечают номера вершин квадратов, а вершины участка закрепляют более надежно – грунтовыми реперами.
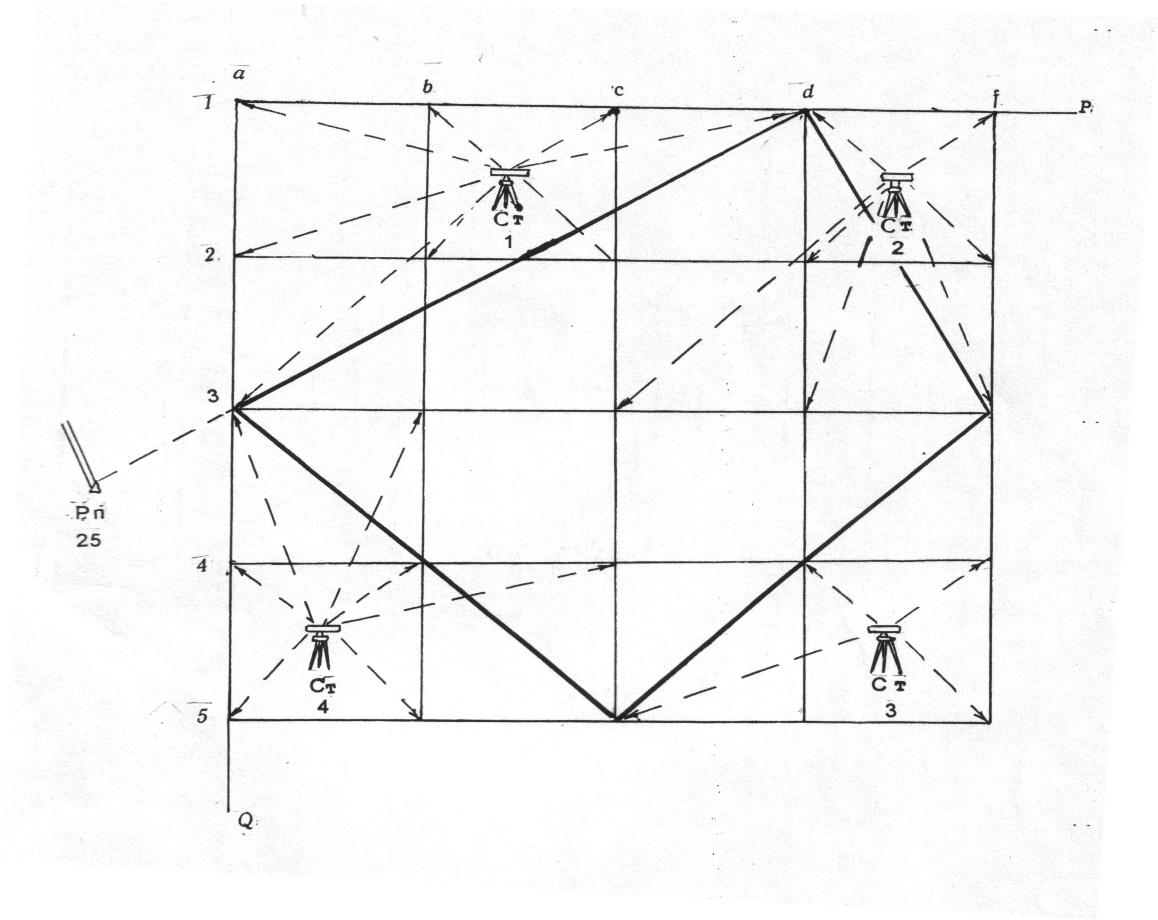
На схеме вершины квадратов отмечаются цифрами, либо цифрами и буквами, либо буквами (рис. 1.1). Места установки нивелиров в квадратах обозначаются буквами или надписью Ст1, Ст2 и т. д. (станция 1, станция 2, …).
Работы начинают от точки А, в которой устанавливают теодолит.
Первоначально, с помощью теодолита, получают направление планируемой линии или более длинной линии по привязке к пунктам опорной сети или к местным предметам. Закрепляют полученное направление в точке Р (рис. 1.1). Одновременно отмеряют и закрепляют вершины квадратов. Затем в точках f1, f5, a5 с помощью теодолита строят прямые углы.
Длину сторон
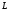 по периметру а1-а5 сравнивают с
теоретическим значением (Lтеор).
Если отношение
по периметру а1-а5 сравнивают с
теоретическим значением (Lтеор).
Если отношение
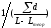 меньше 1:1000, начинают разметку и закрепление
вершин квадратов (здесьd
– периметр участка). Одновременно с
разбивкой и закреплением вершин квадратов
выполняют абрис и намечают плюсовые и
дополнительные точки, направление
скатов местности, границы контуров и
название угодий (лес, пашня и пр.).
меньше 1:1000, начинают разметку и закрепление
вершин квадратов (здесьd
– периметр участка). Одновременно с
разбивкой и закреплением вершин квадратов
выполняют абрис и намечают плюсовые и
дополнительные точки, направление
скатов местности, границы контуров и
название угодий (лес, пашня и пр.).
Рис. 1.1. Схема разметки и нивелирования
при коротких сторонах квадратов
Если необходимо
привязать участок к государственной
или местной сети, то привязку производят
двойным нивелированием. При этом прямое
превышение (hпр)
между пунктом государственной сети и
вершиной квадрата, и обратное превышение
(hобр)
не должны расходиться на величину ±50
мм
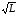 для технического нивелирования, гдеL
– длина линии между геодезическим
пунктом и вершиной квадрата в км.
для технического нивелирования, гдеL
– длина линии между геодезическим
пунктом и вершиной квадрата в км.
Если условие выполняется, определяют среднее превышение (hср) и отметку вершины квадрата (Н) (рис. 1.1):
Hi=HH±hср,
где HH – высота точки, принятой за опорную;
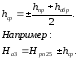
При нивелировании квадратов встречаются два варианта. Первый, когда длина сторон квадратов 50 и более метров.
Нивелирование производят сначала по внешнему кольцу квадратов (на рис. 1.2 – квадраты 1,2,…13, 14), затем по внутреннему (квадраты 15, 16).
Нивелир устанавливают в каждом квадрате, по возможности на диагоналях (рис. 1.3). Нивелируют первоначально два смежных квадрата, и делается в них по четыре взгляда (С, Д, Е, F и K, L, M, N (рис. 1.3)). Определяется превышение между вершинами в1 и в2 в квадрате 1 и 2.
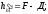 ,
,
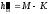
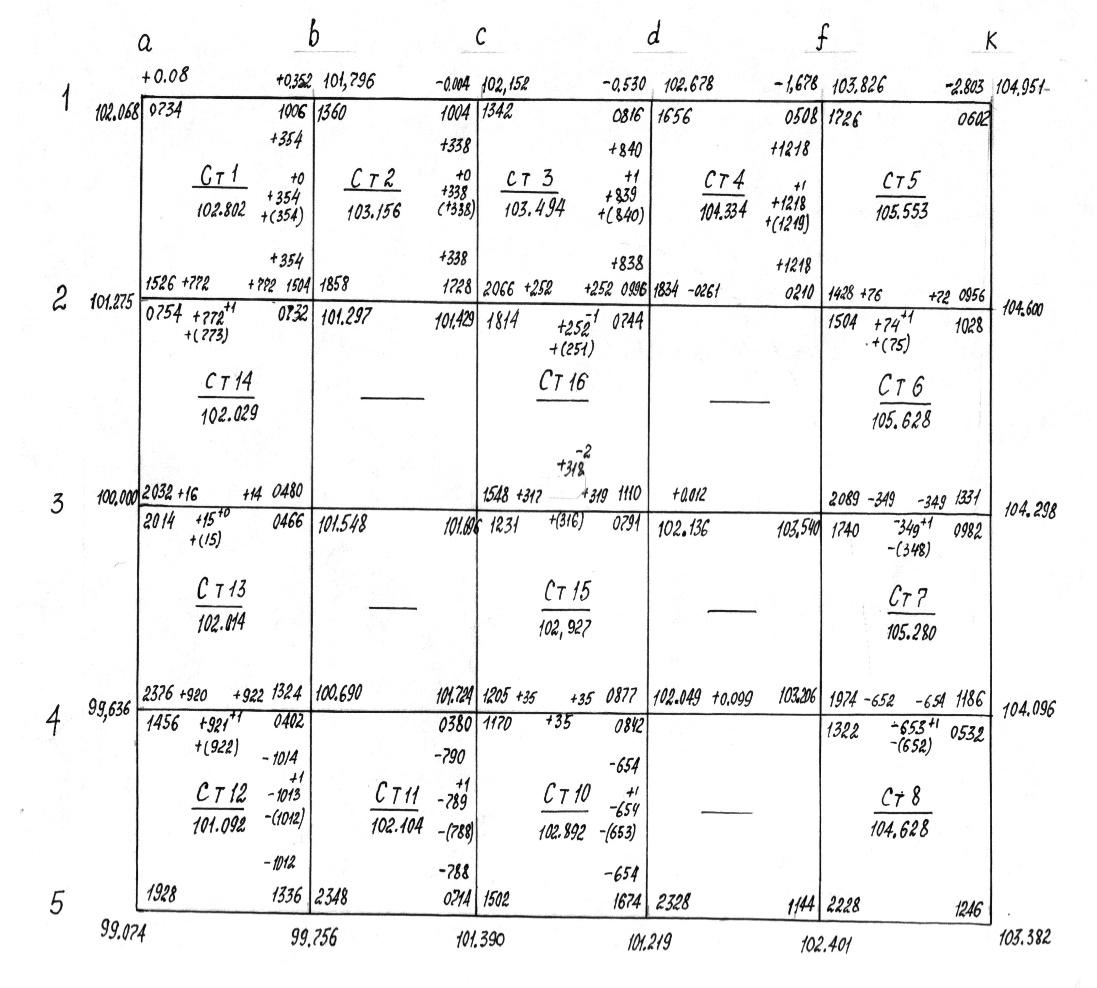
Рис. 1.2. Определение отметок точек при нивелировании квадратов с длинными сторонами
Приравняв выражения и сделав перестановку, получим:
F + K = M + Д.
Таким образом, контролем полевых измерений является равенство сумм накрест лежащих отсчетов. На рис. 1.2 F=1504, K=1360, M=1858, Д=1006. Сумма накрест лежащих отсчетов соответственно, равна 2864 и 2864. Допускается расхождение сумм не более чем на 4 мм.
Второй случай применяется, когда стороны квадратов короткие (20 и менее метров). С одной станции нивелируется по несколько вершинам квадратов (рис. 1.1).
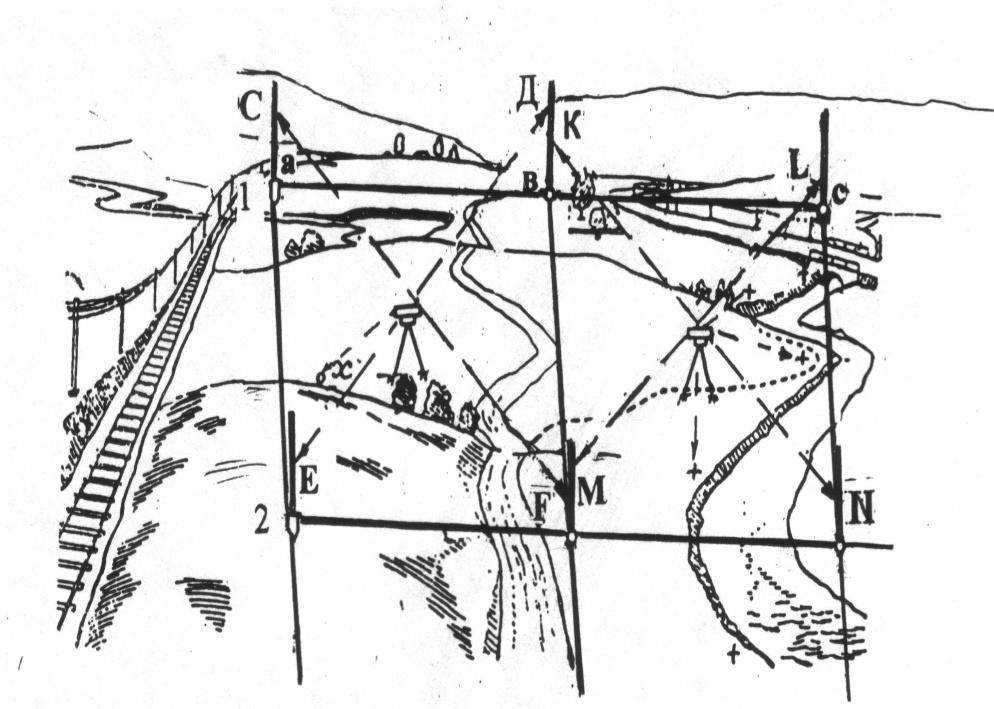
Рис. 1.3. Схема нивелирования квадратов методом из середины
Некоторые вершины квадратов берутся в качестве связующих. На рис. 1.1 в качестве связующих приняты точки a3 – d1 – f3 – c5. Нивелирование по этой магистрали производится более тщательно, и отсчеты берутся по черной и красной сторонам реек (или при двух высотах инструмента).
Журнал нивелирования ведется по обычной форме или результаты нивелирования записывают прямо на схеме (рис. 1.4).
В схеме квадратов стрелкой показывается, по какой диагонали местность идет без искажений. Если при разбивке встречаются объекты, которые не могут быть пронивелированы (рис. 1.3, долина), вблизи этого объекта берутся плюсовые точки, а сам объект нивелируется дополнительно.
При нивелировании квадратов с короткими сторонами схема определения отметок следующая. Первоначально определяют отметки точек нивелирного хода (связующие точки) по общепринятой методике.
На рис. 1.4 отметка точки d1 равна:
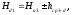
где hср превышение между точками 3 и d, полученное геометрическим нивелированием.
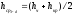 .
.
Превышение
определяется как разность отсчетов по
черной стороне рейки на задней точке
(3ч)
– вершина 3, и передней (Пч)
точке – вершина d.
Контроль-превышение по красной стороне
рейки (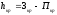 )
не должно отличаться от превышения,
полученного по черной стороне рейки
более чем на 4 мм.
)
не должно отличаться от превышения,
полученного по черной стороне рейки
более чем на 4 мм.
Сумма средних превышений (невязка в превышениях) не должна превышать допустимую
fдоп=10
мм
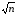 ,
гдеn
– число превышений.
,
гдеn
– число превышений.
Невязку распределяют поровну с обратным знаком, округляя ее до 1 мм.
Исправленная сумма средних превышений в замкнутом нивелирном ходе должна быть равна нулю.
Проиллюстрируем это на примере рис. 1.4.
Превышение между репером 25 и вершиной а3 равно:
в прямом направлении hпр= –701;
в обратном направлении – hобр= –703.
Среднее превышение
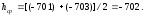

Рис. 1.4. Определение отметок связующих точек
Отметка репера равна 100,833 м, тогда отметка точки а3 будет равна:

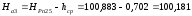 .
.
Среднее превышение между вершинами а3 и d1 равно hср d3=+1437, между вершинами d1 и f3 – hср f3=+894, вершинами f3 и C5 – hср с5= –1164 и между С5 и а3 – hср а3= –1180.
Невязка в превышениях равна:
fh=h=+2331–2344=–13 мм.
Допустимая невязка
fдоп=10
мм
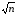 =100
мм
=100
мм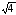 =20
мм.
=20
мм.
Невязка допустима. Ее распределяют поровну с обратным знаком между точками с округлением до 1 мм. Точек 4, тогда поправка
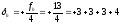
(не должно быть цифр после запятой, т. е. ¾=3,25 , т. к. средние превышения имеют 4 цифы).
Исправленные превышения определяются по формуле:
hиспр=hиспрh.
Согласно приведенному примеру средние исправленные превышения равны:
hср 3–d = +1437+3 = +1440;
hcр f3 = +894+3 = +897;
hср с5 = –1164+3 = –1161;
hср а3 = –1180+3 = –1176.
Исправленная сумма средних превышений равна 1437+897–1161–1176 = 0, что удовлетворяет условию замкнутого нивелирного хода.
После увязки хода определяем отметки связующих точек:
Hd1=100,181+1,440=101,621;
Hf3=101,621+0,897=102,518;
Hc5=102,518–1,161=101,357;
Ha3=101,357–1,176=100,181.
Полученная отметка в конце вычислений, равная начальной, показывает, что вычисления произведены правильно.
Затем определяется горизонт инструмента на каждой станции дважды по формуле:
ГИ=Н+а,
где Н – отметка связующей точки, м; а – отсчет по черной стороне рейки, установленной на этой точке.
На рис. 1.4 горизонт инструмента станции 1 равен:
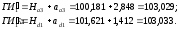
Расхождение между горизонтами инструмента одной станции не должно превышать 5 мм.
Так как на станции 1 условие выполняется, находим среднее значение
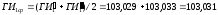 .
.
По такой же схеме определяют горизонты инструментов всех станций. Отметки вершин квадратов определяют, как уже сказано, по формуле:
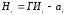 ,
,
где
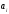 – отсчет по черной стороне рейки на
точке.
– отсчет по черной стороне рейки на
точке.
Обратимся к рис. 1.4. Со станции 1 нивелировались вершины квадратов а1, b1, c1, c2, b2, a2. Отметка вершины а1 равна:
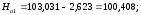
(2,623 – отсчет по
черной стороне рейки в метрах, а в
миллиметрах 2623), а вершины b1
–
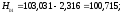
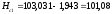 и т. д.
и т. д.
Для контроля можно определить отметку вершины d1 со станции 2
Hd1=103,031–1,412 = 101,619.
Расхождение с ранее определенным значением Hd1, в пределах допустимого.
После вычисления
отметок Hi
всех точек приступают к планировке
участка местности. Планировка производится
горизонтально или под уклоном i.
Сначала вычисляют рабочие отметки
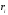 всех точек:
всех точек:
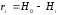 ,
,
где Н0 – проектная отметка условного горизонта горизонтальной плоскости или проектной наклонной плоскости.
Если она не задана, то ее вычисляют по формуле:
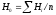 или
или
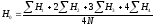 .
.
Первая формула применяется в случаях, когда разность отметок не превышает 0,1 – 0,2 м, вторая – когда необходимо соблюдать баланс выемки и насыпи. В формулах Hi – сумма отметок всех точек; n – число вершин квадратов; N – число квадратов; H2, Н3, Н4 – сумма отметок вершин, общих для двух, трех и четырех квадратов; Н1 – сумма отметок вершин, входящих в один квадрат. На рис. 1.2 – Н1=На1+Hf1+Hf5+Ha5;
H2=Hb1+Hc1+Hd1+Hf2+Hf3+Hf4+Hd5+Hc5+Hb5+Ha4+Ha3+Ha2; H3=0;
H4=Hb2+Hc2+Hd2+Hb3+Hc3+Hd3+Hb4+Hc4+Hd4; n=25.
Нулевая отметка
равна (рис. 1.2) H0=102,148.
Рабочие отметки вершины определяют как
разности между проектной (нулевой) и
фактической отметками. Например, на
рис. 1.2 рабочие отметки вершин
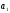 и
и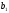 равны:
равны:
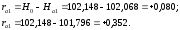
Рабочие отметки подписывают у отметки соответствующей вершины (рис. 1.2, рис. 1.5) слева от проектной отметки. На сторонах квадратов, соединяющих вершины с рабочими отметками (ri), имеющие различные знаки, определяют расстояние до точек нулевых (0) работ (х) по формуле:
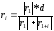 .
.
На рис. 1.5 рабочие отметки с разными знаками находятся в квадратах 2, 3, 16, 20, 19, 9, 10 на сторонах квадратов 1с–2с,2с–2d,2d–3d,3d–3f,4d–4f,4d–5d и 5c–5d. Расстояние до точек нулевых работ на стороне b1 и c1 равно:
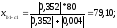
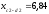 ;
;
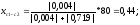
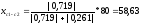 ;
;
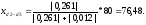
По этой методике определяют расстояния до точек нулевых работ между всеми вершинами с разными знаками.
Здесь 80 – принятая длина стороны квадрата.
Полученные расстояния откладывают в принятом масштабе (на рис. 1.5 М 1:2000) на соответствующих строках и соединяют пунктирной линией, которая является линией нулевых работ. Она служит линией раздела участков насыпей (+) от выемок (–).
Площади выемок показывают красным цветом (на рис. 1.5 – незаштрихованная часть), а площади насыпей – желтым (на рис. 1.5 заштрихованная часть участка).
После определения границы разделения насыпь – срезка определяют объемы земляных работ по методике. Если рабочие отметки всех четырех вершин квадратов имеют одинаковые знаки, то объем грунта:
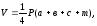
где Р – площадь квадрата; а, в, с, m – соответствующие рабочие отметки.
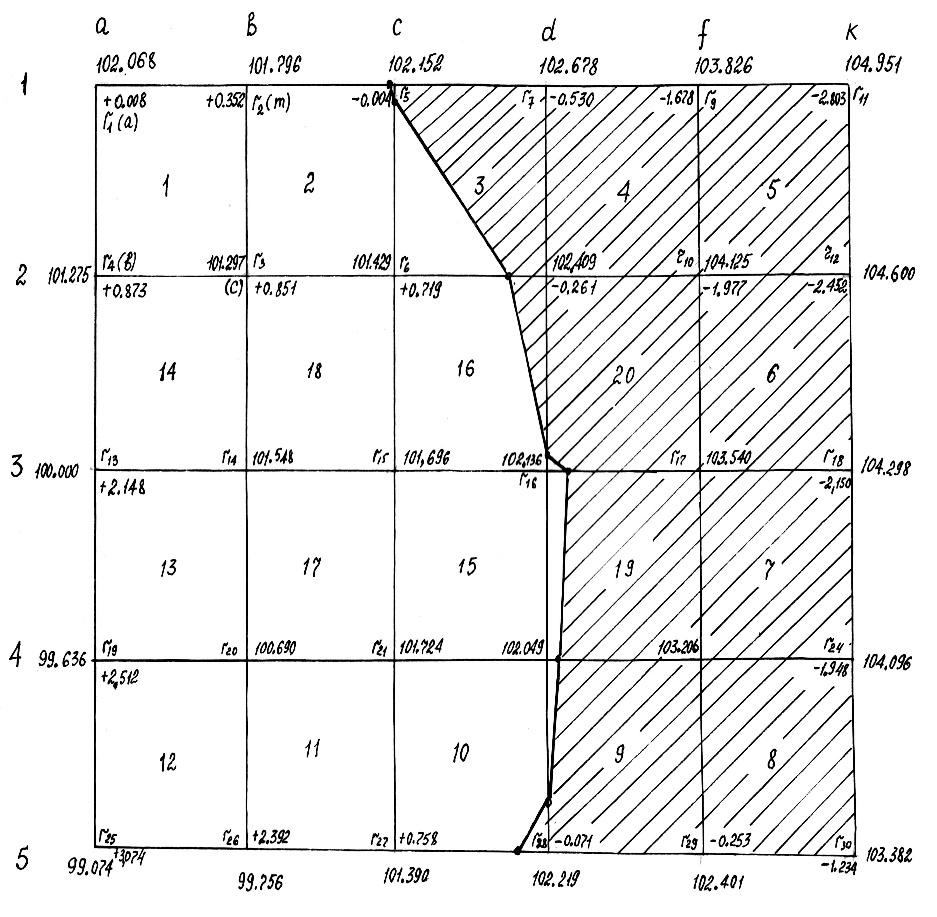
Рис. 1.5. Картограмма земляных работ
Объем земляных работ в первом квадрате (рис. 1.5) равен:
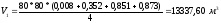 .
.
Если рабочие отметки трех вершин имеют одинаковые знаки, а четвертой противоположный (кв 16, рис. 1.5), то объем равен:
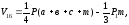
где P1 – площадь треугольника,
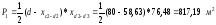 .
.
Объем выемки грунта будет равен:
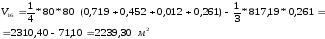
Объем насыпи
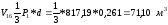 .
.
Если рабочие отметки двух вершин (а, в) имеют одинаковые знаки, а две другие (c, m) – противоположные знаки (квадрат 19, рис. 1.5), то объем насыпи и выемки равны:
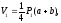
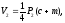
где Р1, Р2 – площади трапеций.
Если рабочие отметки (а, с) по диагонали имеют одинаковые знаки, а две другие (в, m) – противоположные, то объем равен:
выемки
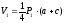 ;
;
насыпи
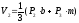 ,
,
где
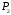 ,
,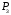 – соответственно площади треугольников,
– соответственно площади треугольников,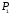 – площадь шестиугольника (рис. 1.6).
– площадь шестиугольника (рис. 1.6).
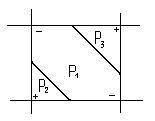
Рис. 1.6. Определение объема земляных работ при одинаковых знаках рабочих отметок по диагонали
При планировке наклонной площадки сначала по заданной проектной отметке Н0 исходной точки и проектным уклонам i0 и i'0 по направлениям сторон квадратов последовательно вычисляют проектные отметки остальных точек вершин квадратов:
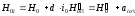 ;
;
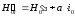 ,
,
где
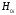 ,
,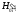 – проектные отметки точек соответственно
в продольном ряду 1–5, 14–6 и т. д. и
поперечном ряду 12–1, 11–2 и т. д.;
– проектные отметки точек соответственно
в продольном ряду 1–5, 14–6 и т. д. и
поперечном ряду 12–1, 11–2 и т. д.;
H'0 – ранее вычисленные проектные отметки в продольном и поперечном рядах.
Затем вычисляют рабочие отметки вершин квадратов по вновь полученным отметкам.
По завершении земляных работ выполняют нивелирование поверхности, оформляют ее в виде плана площадки с указанием фактических отметок точек и их отклонений от проекта.
По отметкам строится также план участка в горизонталях.
Практическая работа № 2. Вынос в натуру элементов инженерных сооружений
При выносе осей сооружения применяются способы: прямоугольных координат; условных прямоугольных координат; полярных координат; комбинированные способы; способ угловой засечки; линейной засечки.
Перед выносом
проекта в натуру определяют точность
построения горизонтальных отрезков
mотн
и углов m для выбора измерительных приборов и
типа теодолита:
для выбора измерительных приборов и
типа теодолита:
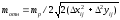 ;
;
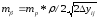 ,
,
где mp – нормативная или проектная точность разбивки; =2*100000’.
Например, при выносе осевой точки О здания АВСД от пункта строительной сетки 1 (рис. 2.1, а), если х1-0=50 м, y1–0=30 м, а mр=5 см, получим mотн=1/3000 и m120"=2'.
Следовательно, построение отрезков х и у можно выполнить рулеткой ОПК-3 3-го класса точности без учета натяжения и температуры, а угла – теодолитом с точностью 1'.
