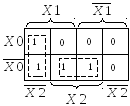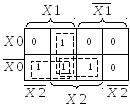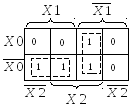2.4. Минимизация недоопределённой фал

ФАЛ называется недоопределённой (частично определённой), если часть её значений y_iне задана (см. п. 1.5). При минимизации такой ФАЛ необязательным значениям, которые обычно обозначают *, можно произвольно присваивать единичные или нулевые значения из условия получения на карте ВейчаКарно минимального числа максимально больших областей.

Рассмотрим пример минимизации ФАЛ, заданной таблицей истинности:

Х3	Х2	Х1	Х0	Y
0	0	0	0	0
0	0	0	1	*
0	0	1	0	*
0	0	1	1	1
0	1	0	0	*
0	1	0	1	*
0	1	1	0	0
0	1	1	1	*
1	0	0	0	*
1	0	0	1	*
1	0	1	0	0
1	0	1	1	*
1	1	0	0	1
1	1	0	1	*
1	1	1	0	*
1	1	1	1	0

Составим карту Вейча – Карно.

Как видно из карты, ни единичные, ни нулевые значения ФАЛ невозможно объединить друг с другом. Поэтому ДНФ имеет вид

, (2.5)

а КНФ

. (2.6)

Предположим, что для доопределения ФАЛ принято решение присвоить всем необязательным значениям функции единичные значения. В результате получим следующий вид карты, на которой выделены области единичных значений, и соответствующую МДНФ.

Очевидно, что такое решение привело к отрицательному результату. Полученная МДНФ оказалась даже сложнее исходной ДНФ (2.5). Поэтому проведём новое доопределение ФАЛ, добавив единичные значения функции только для получения на карте Вейча Карно минимального числа максимально больших областей.

Поскольку выделить область из восьми клеток не удалось, выбрано решение о выделении двух областей из четырёх клеток каждая. Полученное выражение МДНФ проще исходной ДНФ и требует для своей реализации два инвертора, два элемента 2И и один элемент 2ИЛИ.

Теперь проведём доопределение ФАЛ, добавив нулевые значения функции только для получения на карте Вейча Карно минимального числа максимально больших областей.

Аналогично выделяем две области по четыре клетки в каждой, поскольку выделить область из восьми клеток невозможно. Полученное выражение для МДНФ, инверсной заданной, также содержит логическую сумму двух логических произведений. Для реализации потребуется три инвертора (два для переменных и один для функции), два элемента 2И и один 2ИЛИ.

Для дальнейших преобразований воспользуемся теоремой Де-Моргана:

.

В результате получилось выражение существенно проще, чем исходная КНФ (2.6), для реализации которого потребуется два инвертора, два элемента 2ИЛИ и один элемент 2И. Следует также отметить, что в варианте МКНФ не нужна переменная Х2.

Окончательный выбор варианта технической реализации ФАЛ будет зависеть от типа заданных (или имеющихся в наличии) ЛЭ.

2.5. Минимизация системы фал

Если логическое устройство имеет mвыходов, то его структура описывается системойmФАЛ. Минимизация структуры такого устройства может быть выполнена с использованием метода карт Вейча – Карно раздельно для каждого выхода. При этом может оказаться, что структура всего устройства получится неоптимальной.

Достижение оптимального результата может быть реализовано выделением в каждом выражении одинаковых импликант, то есть выделением на картах одинаковых областей. Сформировав такую импликанту только один раз, можно использовать её для нескольких из mуравнений, сократив, таким образом, общее число логических элементов в технической реализации логического устройства.

Рассмотрим пример минимизации системы ФАЛ из трёх функций Y1,Y2,Y3 для трёх переменныхX2,X1,X0 [1], заданных таблицей истинности.

X2	X1	X0	Y3	Y2	Y1
0	0	0	0	0	0
0	0	1	0	0	0
0	1	0	1	1	1
0	1	1	0	0	1
1	0	0	1	1	1
1	0	1	1	0	0
1	1	0	1	1	1
1	1	1	0	1	0

Составим карты Вейча – Карно и проведём минимизацию для получения МДНФ раздельно для каждого выхода.

	.
	.
	.

Техническая реализация системы ФАЛ, уравнения которой получены раздельно для каждого выхода, потребует три инвертора, семь элементов 2И, два элемента 2ИЛИ и один элемент 3ИЛИ, то есть всего 13 элементов.

Если проанализировать полученные уравнения, можно выделить в них общие члены и. Сформировав их только один раз, можно упростить техническую реализацию системы ФАЛ. В этом случае потребуется три инвертора, пять элементов 2И, два элемента 2ИЛИ и один элемент 3ИЛИ, то есть всего 11 элементов. Структурная схема такого логического устройства представлена на рис. 2.4.

Рис. 2.4. Структурная схема ЛУ для Y1, Y2 и Y3

Нетрудно заметить, что для Y1 не использована область, а дляY3область. Эти области при раздельной минимизации получаются лишними. Но если стремиться к получению наилучшего результата минимизации системы ФАЛ, можно добавить эти импликанты в соответствующие уравнения, а затем провести дополнительные преобразования по теоремам алгебры логики:

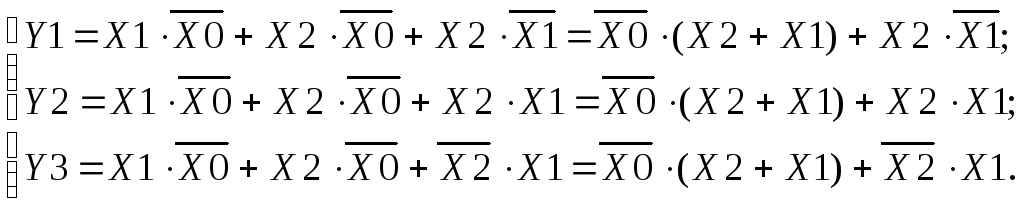(2.7)

Реализация такой схемы логического устройства потребует три инвертора, четыре элемента 2И и четыре элемента 2ИЛИ, то есть тоже 11 элементов. Однако из схемы исключается элемент 3ИЛИ, что является преимуществом, так как упрощает реализацию. Структурная схема такого логического устройства представлена на рис. 2.5.

Рис. 2.5. Структурная схема ЛУ для Y1, Y2 и Y3 по выражению (2.7)

Контрольные вопросы

1. В чём заключается цель минимизации логических устройств?

2. Почему реализация логического устройства по ДНФ или КНФ, полученным непосредственно из таблицы истинности, не будет оптимальной?

3. Почему преобразования по теоремам алгебры логики не всегда могут обеспечить получение минимальной технической реализации логического устройства?

4. Что такое карта Вейча – Карно?

5. Приведите примеры карт Вейча – Карно для двух, трёх и четырёх переменных.

6. Приведите алгоритм минимизации ФАЛ с помощью карт Вейча – Карно.

7. Что такое импликанта?

8. В чём заключается порядок минимизации недоопределённой ФАЛ?

9. Почему замена всех необязательных значений недоопределённой ФАЛ может привести к отрицательному результату минимизации?

10. Почему желательно проводить минимизацию и по единичным и по нулевым значениям ФАЛ?

11. Каковы особенности минимизации системы ФАЛ?

12. Почему минимизация системы ФАЛ раздельно для каждого выхода может привести к неоптимальному результату технической реализации логического устройства в целом?