1.2. Дискретные сигналы

Алфавит дискретных устройств содержит только два знака: 0 (ноль) и 1 (единица). Объём двоичного алфавита определяет объём информации, выражаемый одним символом. В общем виде информацию измеряют в битах и определяют по формуле

, (1.1)

где n– число равновероятных исходов в событии, описываемом дискретным сигналом.

Так как для дискретного сигнала n= 2, тобит– это объём информации, передаваемый одним двоичным символом. Восемь бит образуют одинбайт, то есть в одном байте восемь двоичных разрядов.Кодовое слово, применяемое в алгоритмах обмена информацией в вычислительной технике, содержит четыре байта (32 двоичных разряда) или восемь байт (64 двоичных разряда). Эквивалент кодового слова из 32 единиц двоичной системы счисления в десятичной системе счисления – 4 294 967 296.

Значениям знаков 0 и 1 могут быть поставлены в соответствие различные характеристики токов или напряжений. Например, при потенциальном способеэто могут быть их некоторые установившиеся значения: высокий уровень напряжения – логическая единица, низкий уровень – логический ноль. Временная диаграмма такого дискретного сигнала представлена на рис. 1.1.

Р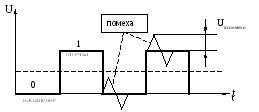ис. 1.1. Временная диаграмма дискретного сигнала

Преимущества дискретного сигнала: малое потребление мощности от источника питания в статическом режиме:

насыщение ;

отсечка

и высокая помехозащищённость: амплитуда помехи U_{m.помехи}может достигать половины величины напряжения сигнала логической единицыU₍₁₎, не вызывая ошибки определения значения сигнала.

1.3. Логические константы и переменные. Логические операции. Логические элементы

Для описания алгоритмов работы дискретных устройств необходим соответствующий математический аппарат. Такой математический аппарат в XIXвеке разработал ирландский математик Джон Буль, и теперь его называют булевой алгеброй (алгеброй логики). Булева алгебра оперирует двумя понятиями: событие истинно (логическая единица – лог. 1) или событие ложно (логический нуль – лог. 0). Эти два понятия называются константами алгебры логики.

Логические переменные могут принимать одно из двух значений констант:

х = 0, если х 1;

х = 1, если х 0.

Над логическими константами и переменными можно совершать логические операции: логическое сложение, логическое умножение и отрицание (инверсию).

Логическое сложение: операция ИЛИ (дизъюнкция). Правило логического сложения для двух переменных представлено в таблице 1.2.

Таблица 1.2

Правило операции логического сложения

Х1	Х0	Х1 + Х0 (Х1 V X0)
0	0	0
0	1	1
1	0	1
1	1	1

Операция логического сложения справедлива для любого числа переменных и соответствует математической операции объединения множеств. Число переменных, над которыми проводится операция, обозначается цифрой, стоящей перед обозначением операции. Для данного примера получаем запись 2ИЛИ.

Логическое умножение: операция И (конъюнкция). Правило логического умножения для двух переменных представлено в таблице 1.3.

Таблица 1.3

Правило операции логического умножения

Х1	Х0	Х1  Х0 (Х1  X0)
0	0	0
0	1	0
1	0	0
1	1	1

Операция логического умножения также справедлива для любого числа переменных и соответствует математической операции пересечения множеств. Число переменных, над которыми проводится операция, также обозначается цифрой, стоящей перед обозначением операции. Для данного примера получаем запись 2И.

Отрицание (инверсия): операция НЕ. Операция обозначается горизонтальной чертой над переменной (или над выражением, содержащим несколько переменных) и определяется правилом:

если , то;

если , то.

Логические элементы. В соответствии с перечнем логических операций различают три основных логических элемента (ЛЭ): И, ИЛИ, НЕ. Условные графические обозначения логических элементов представлены на рис. 1.2.

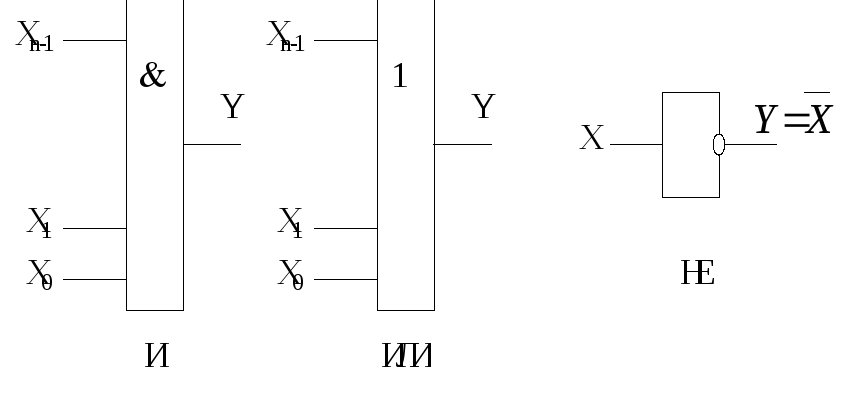
Рис. 1.2. Условные графические обозначения логических элементов

Число входов элементов И и ИЛИ может быть произвольным. Элемент НЕ всегда имеет только один вход.