
- •Минобрнауки россии
- •Содержание
- •Раздел I теория вероятностей 8
- •Раздел II математическая статистика 73
- •Введение
- •Раздел I теория вероятностей
- •Правило суммы
- •Правило произведения
- •Формулы комбинаторики
- •Размещения без повторения
- •Перестановки без повторений
- •Сочетания без повторений
- •Размещения с повторением
- •Сочетания с повторением
- •Перестановки с повторением
- •Лекция 2. Пространство элементарных событий. Классическое определение вероятности
- •Пространство элементарных событий
- •Свойства вероятности
- •Лекция 3. Различные определения вероятностей Статистическое определение вероятности
- •Геометрическая вероятность
- •Парадокс Бертрана
- •Аксиоматическое построение теории вероятностей
- •Лекция 4. Условная вероятность. Теорема умножения. Независимые события. Формула полной вероятности
- •Независимые события. Теорема умножения
- •Формула полной вероятности
- •Формула Бейеса
- •Лекция 5. Независимые испытания. Формула Бернулли.
- •Формула Бернулли
- •Наивероятнейшее число
- •Локальная предельная теорема Муавра-Лапласа
- •Интегральная предельная теорема Лапласа
- •Лекция 6. Дискретная случайная величина и ее числовые характеристики Виды случайных величин. Способы описания дискретной случайной величины
- •Функция распределения
- •Свойства функции распределения
- •Математическое ожидание и дисперсия дискретной случайной величины
- •Свойства математического ожидания дискретной случайной величины
- •Математическое ожидание и дисперсия некоторых случайных величин
- •Лекция 7. Непрерывная случайная величина и её распределения
- •Нормальное (гауссовское) распределение
- •Равномерное распределение
- •Лекция 8. Математическое ожидание, дисперсия, моменты непрерывной случайной величины
- •Закон больших чисел. Теорема Чебышева. Центральная предельная теорема
- •Лекция 9. Некоторые модели законов распределений, наиболее распространенных в практике статистических исследований
- •1. Биномиальное распределение
- •2. Распределение Пуассона
- •3. Нормальное (гауссовское) распределение
- •4. Логарифмически-нормальное распределение
- •5. Экспоненциальное распределение
- •7. Распределение Стьюдента с степенями свободы
- •8. Распределение Фишера-Снедекора (f-распределение).
- •Раздел II математическая статистика Лекция 1. Генеральная совокупность. Выборка. Способы образования выборки. Статистическая оценка параметров распределения.
- •Задача статистической оценки параметров
- •Точечные оценки основных параметров распределений
- •Лекция 2. Законы распределения выборочных характеристик, используемые при оценке параметров. Интервальные оценки параметров распределения.
- •1. Распределение средней арифметической.
- •2. Распределение Пирсона (- хи квадрат).
- •3. Распределение Стьюдента (t-распределение).
- •Интервальная оценка параметра распределения. Понятие доверительного интервала.
- •Интервальные оценки для генеральной средней.
- •Интервальные оценки для генеральной доли
- •Интервальные оценки для генеральной дисперсии и среднего квадратического отклонения
- •Лекция 3. Проверка статистических гипотез о значении параметров распределения. Понятие статистической гипотезы и статистического критерия.
- •1. Проверка гипотезы о значении генеральной средней нормально распределённой совокупности
- •2. Проверка гипотезы о значении генеральной дисперсии нормально распределённой совокупности.
- •3. Вычисление мощности критерия
- •Мощность критерия при проверке гипотезы о значении генеральной средней
- •Мощность критерия при проверке гипотезы о значении генеральной дисперсии
- •Лекция 4 Гипотезы о виде закона распределения генеральной совокупности
- •Вычисление теоретического ряда частот
- •Понятие о критериях согласия
- •Критерий согласия Пирсона
- •Лекция 5. Элементы корреляционного анализа Задачи корреляционного анализа. Двумерная корреляционная модель
- •Примерные вопросы к экзамену
- •Задачи к экзамену
Задачи к экзамену
В партии из 6 деталей имеется 4 стандартных. Наудачу отобраны 3 детали. Составьте закон распределения случайной величины

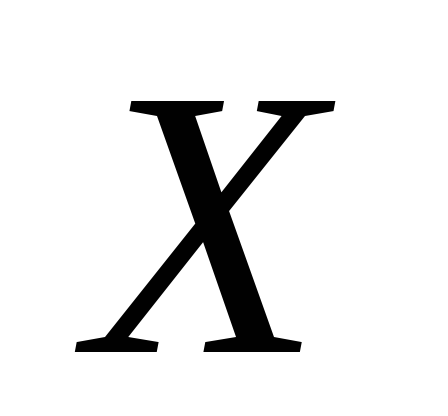 -
числа стандартных деталей среди
отобранных. Найдите математическое
ожидание, и дисперсию этой случайной
величины.
-
числа стандартных деталей среди
отобранных. Найдите математическое
ожидание, и дисперсию этой случайной
величины.Каждый из двух стрелков делает по два выстрела в мишень. Вероятность попадания для первого стрелка равна 0,8, для второго- 0,9. Составьте закон распределения общего числа попаданий. Определите математическое ожидание и дисперсию числа попаданий.
Вероятность поражения мишени стрелком при одном выстреле равна 0,6. Найти вероятность следующих событий:
при 10 выстрелах мишень будет поражена 5 раз;
при 200 выстрелах мишень будет поражена не менее110, но не более 120 раз.
Вероятность поражения мишени стрелком при одном выстреле равна 0,6. Найти вероятность следующих событий:
при 200 выстрелах мишень будет поражена не менее 110 раз;
при 300 выстрелах частость попадания отклонится от вероятности 0,6 не более чем на 0,05 (по абсолютной величине).
В урне 12 шаров, ничем, кроме цвета, не различающихся. Среди них 5 белых и 7 черных. Какова вероятность, что из наудачу вынутых 2 шаров 2 окажутся белыми?
В ящике 15 теннисных мячей, из них 9 новых. Для первой игры было взято 3 мяча. Какова вероятность, что для второй игры все взятые мячи окажутся новыми?
Имеется 10 одинаковых урн, из которых в 9 находится по 2 черных и 2 белых шара, а в одной – 5 белых и 1 черный шар. Из наугад взятой урны извлечен один шар. Чему равна вероятность, что этот шар взят из урны, содержащей 5 белых шаров, если он оказался белым?
Определить наименьшее количество деталей, которое надо проверить, чтобы с вероятностью не меньше 98% можно было ожидать, что абсолютная величина отклонения частости годных деталей от вероятности быть годной, равной 0,95, не превысит 0,01 (применить неравенство Чебышева).
В партии 6 деталей второго сорта и 4 детали первого сорта. Наудачу одна за другой отбираются детали до тех пор, пока деталь не окажется первосортной. Составьте закон распределения числа отобранных при этом деталей. Найдите вероятность того, что будет отобрано не менее 4 деталей.
Диаметр детали, изготовленной цехом, является случайной величиной, распределенной по нормальному закону. Ее дисперсия равна 0,0001
 ,
а математическое ожидание – 2,5 см. Найти
границы, в которых с вероятностью 0,9973
заключен диаметр наудачу взятой детали.
,
а математическое ожидание – 2,5 см. Найти
границы, в которых с вероятностью 0,9973
заключен диаметр наудачу взятой детали.Каждый из двух стрелков делает по два выстрела в мишень. Вероятность попадания для первого стрелка равна 0,8, для второго- 0,9. Составьте закон распределения общего числа попаданий. Определите математическое ожидание и дисперсию числа попаданий.
Вероятность поражения мишени стрелком при одном выстреле равна 0,6. Найти вероятность следующих событий:
при 10 выстрелах мишень будет поражена 5 раз;
при 200 выстрелах мишень будет поражена не менее110, но не более 120 раз.
Вероятность поражения мишени стрелком при одном выстреле равна 0,6. Найти вероятность следующих событий:
при 200 выстрелах мишень будет поражена не менее 100 раз;
при 300 выстрелах частость попадания отклонится от вероятности 0,6 не более чем на 0,05 (по абсолютной величине).
На карточках написаны целые числа от 1 до 15 включительно. Наудачу извлекаются две карточки. Какова вероятность, что сумма чисел, написанных на этих карточках, будет равна 10?
В одном ящике имеется 12 однотипных изделий, из которых 4 нестандартные, В другом 15 деталей и 3 из них нестандартные. Из каждого ящика наудачу извлекают по 2 детали. Найдите вероятность того, что из первого ящика извлекли 2 нестандартные детали, а из второго – 2 стандартные.
На склад поступила продукция трёх фабрик. Объёмы продукции первой, второй и третьей фабрик относятся соответственно как 2:5:3. Известно также, что средний процент нестандартных изделий среди продукции первой фабрики равен 3, второй – 2, третьей – 1%. Найти вероятность того, что наудачу взятое изделие произведено на первой фабрике, если оно оказалось нестандартным.
Найти дисперсию случайной величины Х, заданной интегральной функцией

Случайная величина Х задана интегральной функцией

Найти вероятность того, что в результате испытания величина Х примет значение, заключенное в интервале (0,25; 0,75).
Если график плотности распределения случайной величины Х имеет вид:
 ,
,
то дисперсия D(4Х - 2) =
Если случайная величина X задана плотностью распределения
 тоM(3X+2)
равна…
тоM(3X+2)
равна…Изделие проверяется на стандартность одним из двух товароведов. Вероятность того, что изделие попадет к первому товароведу, равна 0,55, а ко второму – 0,45. Вероятность того, что стандартное изделие будет признано стандартным первым товароведом, равна 0,9, а вторым – 0,98. Стандартное изделие при проверке было признано стандартным. Найти вероятность того, что это изделие проверил второй товаровед.
Игра состоит в набрасывании колец на колышек. Игрок получает 6 колец и бросает кольца до первого попадания. Составить закон распределения числа попадания колец на колышки. Найти вероятность того, что хотя бы одно кольцо останется неизрасходованным, если вероятность попадания при каждом броске равна 0,1лышки.
На основании n=9 испытаний установлено, что в среднем на изготовление полупроводникового диода требуется
 с
иS=3
с. Предположив, что время изготовления
диода есть нормальная случайная
величина, определите с надежностью
с
иS=3
с. Предположив, что время изготовления
диода есть нормальная случайная
величина, определите с надежностью
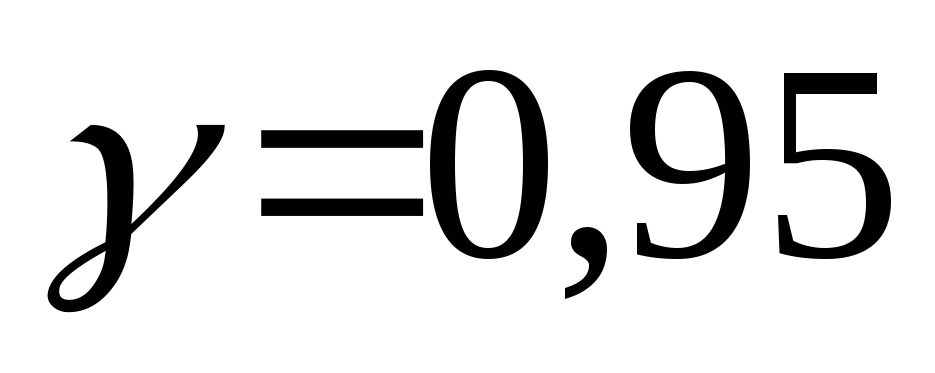 доверительный интервал для генеральной
средней
доверительный интервал для генеральной
средней .
.На основании n=9 испытаний установлено, что в среднем на изготовление полупроводникового диода требуется
 с
иS=3
с. Предположив, что время изготовления
диода есть нормальная случайная
величина, определите с надежностью
с
иS=3
с. Предположив, что время изготовления
диода есть нормальная случайная
величина, определите с надежностью
 доверительный интервал для генерального
среднего квадратического отклонения
доверительный интервал для генерального
среднего квадратического отклонения .
.Средняя урожайность пшеницы на 17 опытных участках области составила:
 ,
а
,
а .
Найдите с надежностью 0,975 границы
доверительного интервала для оценки
генеральной средней.
.
Найдите с надежностью 0,975 границы
доверительного интервала для оценки
генеральной средней.Средняя урожайность пшеницы на 17 опытных участках области составила:
 ,
а
,
а .
Найдите, в предположении о нормальном
распределении вероятность того, что
среднее квадратическое отклонение
генеральной совокупности находится в
интервале (0,9S;
1,1S).
.
Найдите, в предположении о нормальном
распределении вероятность того, что
среднее квадратическое отклонение
генеральной совокупности находится в
интервале (0,9S;
1,1S).Партия изделий принимается, если дисперсия контролируемого размера не превышает 0,2. По выборке
 изделий
вычислена дисперсия,
изделий
вычислена дисперсия, Можно ли принять партию при уровне
значимости
Можно ли принять партию при уровне
значимости ?
?Поставщик ламп накаливания утверждает, что средний срок службы лампы равен 2500 ч. Для выборки из 37 ламп средний срок службы оказался равным 2325 ч при среднем квадратическом отклонении 600 ч. Проверьте справедливость утверждения поставщика при
 .
.На основании 12 измерений найдено, что средняя высота сальниковой камеры равна:
 а
а .
Проверьте на уровне значимости 0,01
нулевую гипотезу
.
Проверьте на уровне значимости 0,01
нулевую гипотезу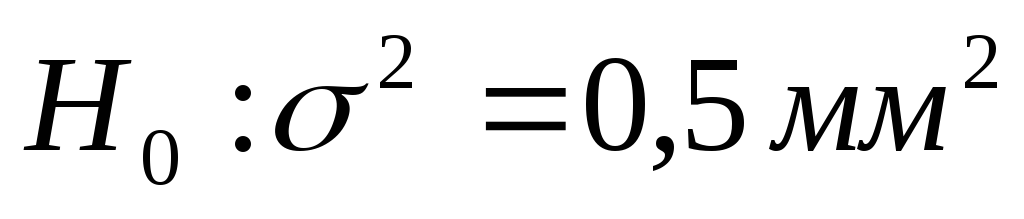 ,
при конкурирующей гипотезе
,
при конкурирующей гипотезе .
.На основании 12 измерений найдено, что средняя высота сальниковой камеры равна:
 а
а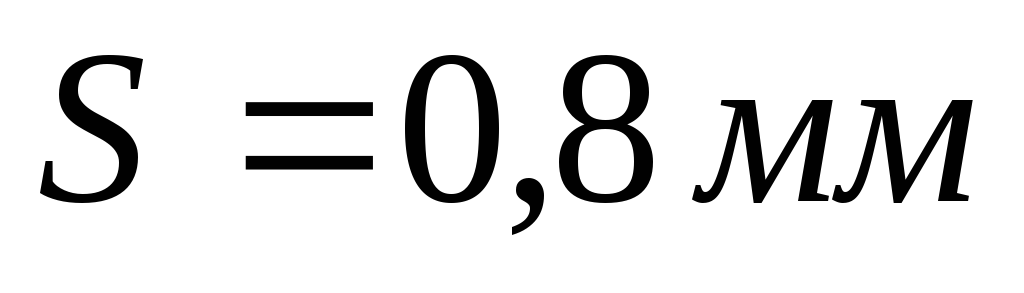 .
Проверьте на уровне значимости 0,01
нулевую гипотезу
.
Проверьте на уровне значимости 0,01
нулевую гипотезу ,
при конкурирующей гипотезе
,
при конкурирующей гипотезе .
.На основании 12 измерений найдено, что средняя высота сальниковой камеры равна:
 а
а .
Проверьте на уровне значимости 0,01
нулевую гипотезу
.
Проверьте на уровне значимости 0,01
нулевую гипотезу ,
при конкурирующей гипотезе
,
при конкурирующей гипотезе .
.
