2. Проверка гипотезы о значении генеральной дисперсии нормально распределённой совокупности.

Пусть из генеральной совокупности, значения которой распределены по нормальному закону с неизвестной дисперсией , взята случайная выборка изn независимых наблюдений и вычислена выборочная дисперсия S².

Требуется проверить нулевую гипотезу , где- определённое значение генеральной дисперсии. Для проверки нулевой гипотезы используют статистику

, (10)

которая при выполнении гипотезы имеет распределениесстепенями свободы.

В зависимости от конкурирующей гипотезы рассматривают левостороннюю, правостороннюю или двустороннюю критические области. Границы критических областей определяют по таблице распределения - Пирсона.

Рассмотрим три случая:

1. Если , то выбирают правостороннюю критическую область инаходят из условия

.

Правила проверки гипотезы заключаются в следующем:

1) если , то нулевая гипотеза не отвергается;

2) если , то нулевая гипотеза отвергается.

2. Если , то строят левостороннюю критическую область инаходят из условия

.

Правила проверки гипотезы заключаются в следующем:

1) если , то гипотеза не отвергается;

2) если , то гипотеза отвергается

3. Если , то строят двустороннюю критическую область и её границыинаходят из условий:

;

Правила проверки гипотезы заключается в следующем:

Если , то гипотеза не отвергается, в противном случае отвергается.

Пример 1. Точность работы автоматической линии проверяют по дисперсии контролируемого признака, которая не должна превышать 0,1 мм². По результатам выборочного контроля получены следующие данные:

Контролируемый размер xi	43,0	43,5	43,8	44,4	44,6
Частота mi	3	7	10	8	2

Требуется проверить на уровне значимости 0,01, обеспечивает ли линия требуемую точность.

Решение: Задача состоит в проверке гипотезы о значении генеральной дисперсии . Автоматическая линия не обеспечивает требуемую точность, если, следовательно, в данном случае строим правостороннюю критическую область.

Для вычисления статистики по формуле (10), необходимо найти выборочную дисперсию. Примем значениеC = 43,8, а вычисление оформим в таблице:

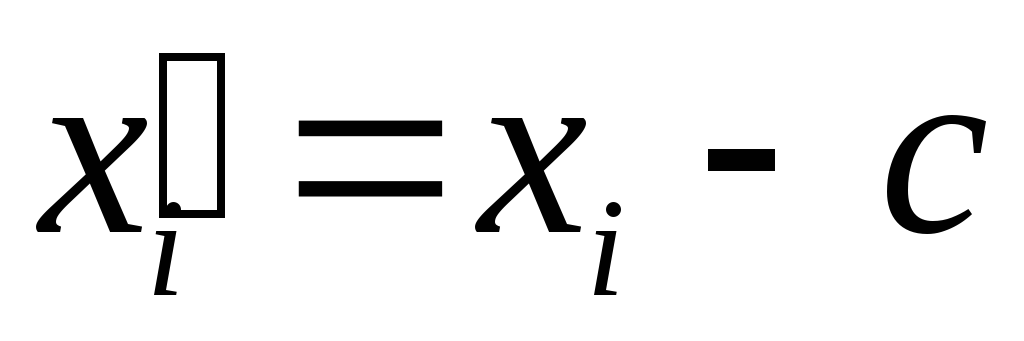
43,0	3	- 0,8	- 2,4	1,92
43,5	7	- 0,3	- 2,1	0,63
43,8	10	0	0	0
44,4	8	0,6	4,8	2,88
44,6	2	0,8	1,6	1,28
Итого:	30	-	1,9	6,71

По таблице - распределения при заданном уровне значимостииполучаем.

Сравнивая и, делаем вывод о том, что гипотезаотвергается. Это значит, что генеральная дисперсия не равна 0,1, линия не обеспечивает заданную точность и требуется её регулировка.

3. Вычисление мощности критерия

Мощность критерия может быть вычислена только при проверке простых гипотез: гипотезы о значении генеральной средней и гипотезы о генеральной дисперсии и только при односторонней критической области.