Лекция 3. Проверка статистических гипотез о значении параметров распределения. Понятие статистической гипотезы и статистического критерия.

Статистической гипотезой называют любое предложение о виде неизвестного закона распределения случайной величины или значении его параметров.

Пусть - закон распределения случайной величины Х, зависящей от одного параметра. Предположим, что надо проверить гипотезу о том, что. Назовём эту гипотезу нулевой (проверяемой) и обозначим её через. Противоположную гипотезу, например,, назовём конкурирующей и обозначим через.

Задача заключается в проверке гипотезы относительно конкурирующей гипотезына основании выборки, состоящей изn независимых наблюдений .

Принцип проверки заключаются в следующем: всё множество выборок объёмом n можно разбить на два непересекающихся подмножества (обозначим их через Q и W) таких, что проверяемая гипотеза должна быть отвергнута, если наблюдаемая выборка попадает в подмножество W, и принята, если наблюдаемая выборка принадлежит подмножеству Q. Подмножество W называют критической областью, Q – областью допустимых значений.

Вывод о принадлежности данной выборки тому или иному подмножеству делают на основании статистического критерия.

Основой критерия является специально составленная выборочная характеристика (статистика) , точное или приближённое распределение которой известно.

Если наблюдаемое значение статистики критерия попадает в критическую область, то гипотезу отвергают, если же оно попадает в область допустимых значений, то гипотезу не отвергают.

При использовании этого принципа возможны ошибки двух видов:

- гипотеза H₀ верна, но её отвергают согласно критерию, т.е.

допускается ошибка, которую принять называть ошибкой первого рода;

-гипотеза H₀ неверна, и её принимают согласно критерию, т.е.

допускается ошибка второго рода.

Уровнем значимости называют вероятность совершить ошибку первого рода. С уменьшениемвозрастает вероятность ошибки второго рода.

Мощностью критерия называют вероятность того, что нулевая гипотезаH₀ будет отвергнута, если верна конкурирующая гипотеза, т.е. вероятность не допустить ошибку второго рода.

Обозначим через вероятность попадания статистики критерияв критическую областьW, если верна соответствующая гипотеза H.

Тогда требования к критической области можно выразить следующим образом:

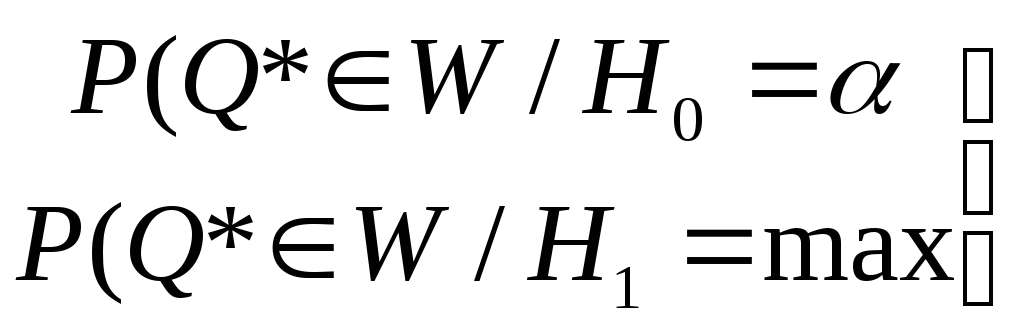(1)

Таким образом, критическую область надо выбирать так, чтобы вероятность попадания в неё статистики была минимальна, если гипотеза H₀ верна, и максимальна в противном случае.

В зависимости от конкурирующей гипотезы H₁ выбирают правостороннюю, левостороннюю или двустороннюю критические области.

Границы областей находят из следующих условий:

при правосторонней критической области

(2)

при левосторонней критической области

(3)

при двусторонней критической области

(4)

1. Проверка гипотезы о значении генеральной средней нормально распределённой совокупности

Пусть из генеральной совокупности X, значения признака имеют нормальный закон распределения с параметрами при неизвестном математическом ожидании, взята случайная выборка объёмаn и вычислена средняя арифметическая , а

и - определённые значения параметра. Для проверки нулевой гипотезыпри конкурирующей гипотезе, в случае, когда значениегенеральной совокупностиизвестно, используется статистика

, (5)

которая при выполнении нулевой гипотезы имеет нормированное нормальное распределение .

Согласно требованию к критической области при выбирают правостороннюю критическую область, при- левостороннюю, при- двустороннюю критическую область.

Границы критической области определяют по интегральной функции Лапласаиз условий:

в случае односторонней критической области:

, (6)

в случае двусторонней критической области:

. (7)

При проверке гипотезы принеизвестной генеральной дисперсии используется статистика

, (9)

которая при выполнении нулевой гипотезы имеет распределение Стьюдента с числом степеней свободы равном .

Границы критической области определяют по таблицеt-распределения для заданного уровня значимости при двусторонней критической области или, если область односторонняя, и числом степеней свободы.

Правила проверки гипотезы сводятся к следующему:

1) при левосторонней критической области, если , нулевая гипотеза не отвергается;

2) при правосторонней критической области, если , то

нулевая гипотеза не отвергается;

3) при двусторонней критической области, если , то нулевая гипотеза не отвергается.

При выполнении противоположных неравенств нулевая гипотеза отвергается.