7. Распределение Стьюдента с степенями свободы

(t-распределение)

В нормальном распределении средняя арифметическая зависит от дисперсии слагаемых величин. Однако на практике дисперсия исследуемой величины, как правило, неизвестна. В этой связи возникла задача определения закона распределения , не зависящего от, которую решил английский статистик В. Госсет, публиковавшийся под псевдонимом Стьюдент. Дадим следующее определение:

Если случайная величина Z имеет нормальное нормированное распределение N(0,1), а величина U² имеет распределение сстепенями свободы, причемZ и U взаимно независимы, то случайная величина

имеет t-распределение с степенями свободы. Плотность распределения описывается формулой

.

Функция плотности является унимодальной и симметричной относительно . Основные числовые характеристики:

среднее, мода, медиана: ;

дисперсия: ;

асимметрия: ;

эксцесс: .

Ниже на рисунке приведены сравнительные графики функции плотности t-распределения при и стандартного нормального распределенияN(0,1).

Рис. 9.2.График t-распределения при и нормального нормированного распределения

Если из генеральной совокупности Х с нормальным законом распределения взята случайная выборка объёмаn, то статистика

имеет распределение Стьюдента с степенями свободы. ЗдесьS-выборочное среднее квадратическое отклонение.

Распределение Стьюдента используется при интервальной оценке математического ожидания при неизвестном значении среднего квадратического отклонения .

8. Распределение Фишера-Снедекора (f-распределение).

Пусть имеются две независимые случайные величины иимеющие-распределение соответственно со степенями свободыи. Тогда величина

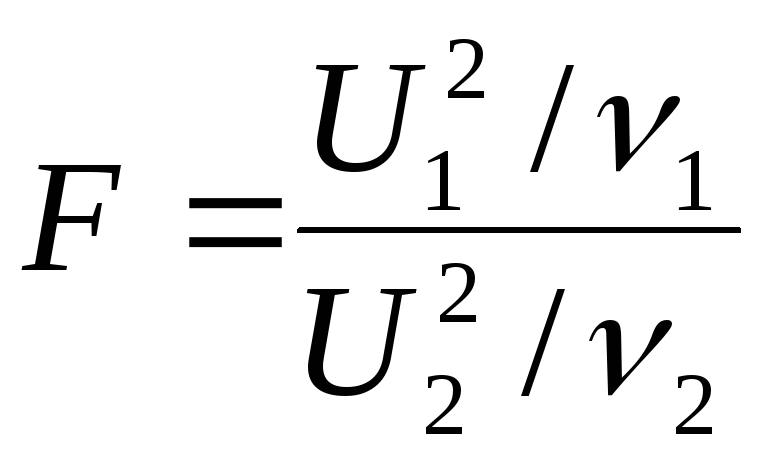
имеет F-распределение с истепенями свободы, причем, так что.

Это распределение впервые было построено английским статистиком Р. Фишером. Американский статистик Дж. Снедекор составил таблицы для данного распределения, поэтому его часто называют распределением Фишера-Снедекора.

Используется в дисперсионном анализе при проверке статистических гипотез.

Раздел II математическая статистика Лекция 1. Генеральная совокупность. Выборка. Способы образования выборки. Статистическая оценка параметров распределения.

В математической статистике множество возможных значений случайной величины Х называют генеральной совокупностью случайной величины Х или просто генеральной совокупностью Х.

Исходным материалом для изучения свойств генеральной совокупности являются экспериментальные (статистические) данные, под которыми понимают значения случайной величины, полученные в результате независимых повторных наблюдений (имеется ввиду, что эксперимент может, хотя бы теоретически, быть повторен сколько угодно раз в одних и тех же условиях).

Совокупность независимых случайных величин Х₁, … , Х_{n ,} имеющих на множествах исходов 1, … , n-го экспериментов (наблюдений) то же распределение, что и случайная величина Х, называется случайной выборкой. При этом число n называют объемом выборки. Любое возможное значение (х_{1 , … ,} х_n) случайной выборки - эмпирическим рядом, а числа х_i его вариантами. При этом некоторые варианты могут повторяться. Число повторений вариант называют эмпирической частотой и обозначают n_i (или m_i). Таблица, в которой варианты записаны по одному разу и в порядке возрастания, а также указаны их частоты или частости , называемыевесами, называется вариационным дискретным рядом.

Пример 1. В течении суток измеряют напряжение Х тока в электросети в вольтах. В результате опыта получена выборка объема n = 30:

107 108 110 109 110 111 109 110 111 107

108 109 110 108 107 110 109 111 111 110

109 112 113 110 106 110 109 110 108 112

Построим вариационный ряд этой выборки.

Наименьшее значение в выборке х₁ = 106, наибольшее – х₈ = 113. Подсчитываем частоту каждого х_i, i = 1,…, 8 и строим таблицу 1.1.

хi	106	107	108	109	110	111	112	113
ni	1	3	4	6	9	4	2	1

При большом объеме выборки ( свыше 50 ) исходные данные рассматривают на интервале J = ( х_1, х_n). Этот интервал разбивают на m промежутков равной длины . При этом считают, что каждый промежуток содержит свой левый конец, но лишь последний содержит и правый. При таком соглашении каждая точка отрезкаJ содержится в одном и только в одном интервале J_k. Далее, для каждого промежутка J_k, k = 1,…, m подсчитывается число элементов выборки попавших в него, а результаты представляют в виде таблицы 1.2., которую называют интервальным рядом.

Таблица 1.2.

J1	J2	. . .	Jm
n1	n2	. . .	nm

В зависимости от того, является ли генеральная случайная величина Х дискретной или непрерывной, результаты выборки записывают в виде вариационного или интервального рядов. Для интервального ряда вводят понятие эмпирической плотности распределения, как функции, определяемой формулой:

и равна 0, если .

График функции плотности называют гистограммой.