Интегральная предельная теорема Лапласа

Пусть событие А в каждом из n независимых испытаний наступает с постоянной вероятностью р. Тогда вероятность того, что при достаточно большом числе испытаний событие А наступит от m₁ до m₂ раз вычисляется по формуле:

, (8)

где

(9)

Функцию Ф(х) называют интегральной функцией Лапласа. Её значения табулированы. Рассмотрим некоторые свойства интегральной функции Лапласа.

Свойства функции Ф(х):

1) Ф(х) – нечетная функция, т.е. Ф(-х) = -Ф(х).

2) Ф(х) имеет две горизонтальные асимптоты y = 0,5 и y = -0,5.

Действительно,

В последнем равенстве использовался так называемый интеграл Пуассона:

Ввиду нечетности функции Лапласа

Причем приближение к числу 0,5 настолько быстрое, что для практических целей достаточно при считать значениеФ(х) = 0,5.

3) Из свойства интеграла с переменным верхним пределом от непрерывной функции следует равенство

Пример: Вероятность поражения мишени стрелком равна 0,75. Определить вероятность того, что при 100 выстрелах он поразит мишень:

а) не менее 71, но не более 80 раз;

б) не менее 81 раза.

Решение: Обозначим p = 0,75, n = 100, m – число попаданий в мишень. Тогда

a)

б)

В статистике вероятность р наступления события А заменяют его частостью , причем чем большеn, тем меньше значение частости отклоняется от значения вероятности. Однако сколь тесной окажется эта близость предугадать невозможно. Тем не менее, имеет место следующая теорема.

Теорема Бернулли: Для любого положительного числа справедливо равенство

(10)

Доказательство: ,

тогда

Учитывая свойство (2) функции Ф(х) и переходя к пределу при , получим равенство (10). Теорема Бернулли представляет собой одну из первых формулировок Закона больших чисел.

Замечания: Итак, мы рассмотрели различные случаи изменения величин n, m, p. Каждому из них соответствовала своя предельная теорема. При этом надо руководствоваться следующим:

1) Формулы Бернулли, Лапласа и Пуассона применяются в тех случаях, когда испытания удовлетворяют схеме Бернулли, т.е.

а) проводимые испытания независимы;

б) каждое испытание имеет только два исхода, либо наступает событие А, либо противоположное ему событие;

в) вероятность появления события А в каждом испытании постоянна и равна р.

2) Если число испытаний не велико, то для вычисления вероятности применяют формулу Бернулли.

3) Если n мало и требуется найти вероятность появления события А от m₁ до m₂ раз, то применяют формулу

(11)

4) Если n достаточно велико, и вероятность наступления события А также не маленькая то вычисляется по формуле Лапласа (6).

5) Если n велико, а р – мало, то используют асимптотическую формулу Пуассона (7).

6) Если число испытаний n достаточно велико, то

а) при малом числе слагаемых в сумме (11) и применяют формулу

(12)

б) при малом числе слагаемых и малом р

(13)

в) при большом числе слагаемых в сумме

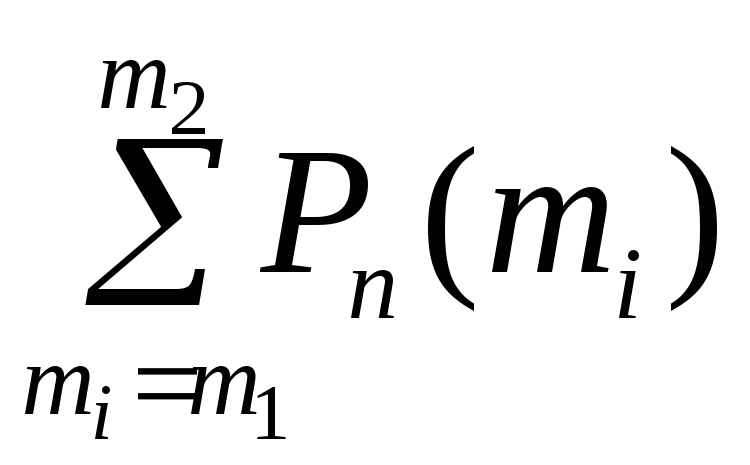
применяют интегральную формулу Лапласа (8).