Лекция 4. Условная вероятность. Теорема умножения. Независимые события. Формула полной вероятности

Определение 1. Вероятность события А, вычисленную в предположении, что событие В наступило, называют условной вероятностью и обозначают P_B(A) или P(A/B).

Проследим за различием безусловной и условной вероятности на примере.

Пример 1. Из колоды в 36 карт последовательно вынимают две карты. Найти:

1. безусловную вероятность того, что вторая карта окажется тузом;

2. условную вероятность, что вторая карта окажется тузом, если первая карта была туз.

Решение: Обозначим через событие А – появление туза на втором месте, а через событие В – появление туза на первом месте. Тогда

1. событие А можно представить в виде следующей суммы несовместных событий:

,

.

2. Если предположить, что первая вытащенная карта – туз, т.е. событие В наступило, то условная вероятность равна

.

Рассмотрим решение задачи отыскания условной вероятности в общем виде для классического определения: Пусть из полной группы попарно несовместных и равновозможных событий А₁, А₂, … , А_n, событию А благоприятствуют m исходов, событию В – k исходов и событию АВ – r исходов данной группы событий.

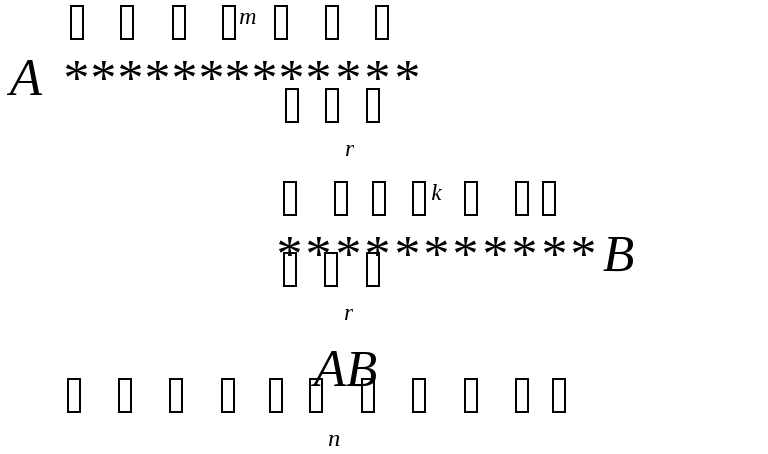
Если событие В произошло, то это означает, что наступило одно из k событий A_j, благоприятствующих событию В. При этом условии событию А благоприятствуют r и только r событий A_j, благоприятствующих событию АВ. Тогда

.

Аналогично доказывается, что

.

Из полученных формул находим, что

P(AB) = P(B)P(A/B) = P(A)P(B/A) (1)

Таким образом доказана теорема умножения:

Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, при условии, что первое событие наступило.

Следствие: Вероятность произведения нескольких событий равна произведению вероятности одного из них на условные вероятности всех остальных, при условии, что все предыдущие события наступили.

(2)

Пример 2. В урне лежат 5 белых, 4 черных и 3 синих шаров. Каждое испытание состоит в том, что извлекается наудачу один шар, не возвращая его обратно. Найти вероятность того, что при первом испытании появится белый шар, при втором – черный, при третьем – синий.

Решение: Обозначим вероятности появления шаров в последовательных испытаниях через Б, Ч, С. Тогда

Условная вероятность обладает всеми свойствами вероятностей, так как она удовлетворяет системе аксиом 1-3.

Действительно:

1) Для любого А определена неотрицательная функция

.

2) Событие А при условии наступления события В будет достоверным, если .

Действительно: .

3) Если А₁, А₂, …, А_n попарно несовместны, то

Независимые события. Теорема умножения

Определение 2. Событие А независимо от события В, если его условная вероятность совпадает с безусловной, т.е.

P(A/B) = P(A)

Теорема 1. Если событие А независимо от события В, то и событие В не зависит от события А.

Действительно: .

Пример 3. В урне лежат3 белых и 5 черных шаров. Последовательно извлекают два шара. Сравним два события:

А – извлеченный шар во втором испытании – белый,

В – извлеченный шар в первом испытании – белый,

если

а) первый шар возвращают обратно в урну перед вторым испытанием,

б) первый шар не возвращают обратно в урну.

Тогда в случае

а) ;;

Таким образом, P(A/B) = P(A), следовательно, события независимы.

б) , следовательно события А и В зависимы.

Теорема 3. Если события А и В независимы, то независимы и каждые два события

Определение 3. События А₁, А₂, …, А_n называются попарно независимыми, если независимы всякие два из них, т.е.

Определение 4. События А₁, А₂, …, А_n называются независимыми в совокупности или просто независимыми, если независимы каждое из них и любое произведение остальных, т.е.

Замечание: Из независимости в совокупности следует попарная независимость событий. Обратное утверждение неверно. Приведем пример Бернштейна:

Пусть грани тетраэдра окрашены в разные цвета: первая грань в красный цвет, вторая в зеленый, третья в синий, четвертая во все три цвета. Производится подбрасывание тетраэдра, который может упасть на одну из граней. Обозначим через события А, В, С падение тетраэдра, соответственно, на красны, зеленый или синий цвета.

Покажем, что события А, В, С попарно независимы, но не являются независимыми в совокупности.

,

,

Таким образом, события попарно не зависимы. Однако

.

Без доказательства сформулируем следующие теоремы.

Теорема 4. Если события А₁, А₂, …, А_n независимы в совокупности, то какова бы ни была группа , составленная из этих событий, вероятность наступления всех событий этой группы равна произведению вероятностей каждого из них, т.е.

.

Имеет место и обратная теорема.

Теорема 5. События А₁, А₂, …, А_n независимы в совокупности, если для любой группы событий

.

Пример 4. Вероятность попадания в цель из первого орудия равна 0,9, из второго – 0,8, из третьего – 0,7. Найти вероятность того, что при одновременном залпе из трех орудий, будет иметь место:

1). Одно поражение цели.

2). Хотя бы одно поражение цели.

Решение: Обозначим через событие А_i – поражение цели i-м орудием, i = 1,2,3. Тогда

1) Событие А – одно поражение цели.

2) Событие А – хотя бы одно поражение цели.

- ни одного попадания в цель. Тогда

Теорема 6. Вероятность наступления хотя бы одного из n независимых событий равна разности между единицей и произведением вероятностей противоположных событий.

Следствие: Если вероятность наступления каждого события одинакова, т.е. P(A_i) = p, , то

.