Аксиоматическое построение теории вероятностей

До начала 30-х годов прошлого столетия теория вероятностей представляла собой еще не сложившуюся математическую науку, в которой основные понятия были недостаточно четко определены. Развитие естествознания предъявило к теории вероятностей повышенные требования. Возникла необходимость в математическом изучении основных понятий теории вероятностей и выяснении тех условий, при которых возможно использование ее результатов. Поэтому особенно важной оказалась задача формально-логического обоснования теории вероятностей, а именно ее аксиоматическое построение. Рассмотрим такое построение, предложенное в 1929 году советским математиком А.Н. Колмогоровым

Будем исходить из некоторого множества U. Элементы этого множества назовем элементарными событиями, а само множество U - пространством элементарных событий.

Рассмотрим систему F подмножеств множества U, удовлетворяющую следующим требованиям:

1) Система F в качестве элемента содержит само множество U.

2) Если два подмножества А и В множества U принадлежат системе F, то ей принадлежат и множества А+В, АВ, . При этом считают:,,.

Далее, так как , то согласно условию 2) будем считать, что, т.е. пустое множество.

Элементы системы F называются случайными событиями, а сама система F называется полем событий.

Событие U называется достоверным событием. Пустое множество V называется невозможным событием.

Два события А и В называются несовместными, если их произведение является невозможным событием, т.е. .

События А и называются противоположными.

3) Если А₁,А₂,…,А_n,… подмножества множества U являются элементами системы F, т.е. , тои.

В этом случае систему F называют борелевским полем событий (т.е. замкнутым относительно теоретико-множественных операций, производимых в счетном числе).

Аксиома 1. Каждому случайному событию А из поля F ставится в соответствие неотрицательное число P(A), называемое его вероятностью.

Аксиома 2. Вероятность достоверного события U равна 1.

Аксиома 3. Для любого конечного или счетного множества попарно несовместных событий А₁,А₂,…,А_n,… из поля F

Следствия системы аксиом:

1) Вероятность невозможного события V равна нулю, т.е. P(V) = 0.

U = U+V, P(U) = P(U)+P(V) следовательно P(V) = 0.

2) Для любого события выполняется равенство

3) Для любого события ,.

Действительно, из аксиомы 1 следует, что , по следствию 2). Тогда.

4) Если , то.

Действительно, событие В можно рассматривать как сумму двух несовместных событий: , тогда по аксиоме 3

5) Для любых двух событий А и В из поля F, выполняется равенство:

Доказательство: Используя теоретико-множественные методы, легко проверить равенства

Используя несовместность событий

, из аксиомы 3 имеем

^*

Подставляя полученные выражения вероятностей в правую часть равенства (*), найдем:

.

В частности, если , то.

Совокупность множества U-элементарных событий, поля F случайных событий и определенной на нем вероятности случайного события P(A), называют вероятностным пространством и обозначают (U,F,P).

Замечания:

1) Система аксиом Колмогорова непротиворечива, так как существуют реальные объекты, которые этим аксиомам удовлетворяют.

Например, пусть U = {a₁, a₂, …, a_n} - произвольное множество. За F возьмем совокупность всех подмножеств , где. Тогда положив

,

где и, а, мы удовлетворим всем аксиомам Колмогорова.

2) Система аксиом Колмогорова неполна.

Даже для одного и того же множества U можно по-разному выбирать вероятности во множестве F.

Например, в полной группе событий U = {E₁, E₂, …,E₆}, где E_i – выпадение i очков на грани игральной кости, можно считать, что

(1)

Или

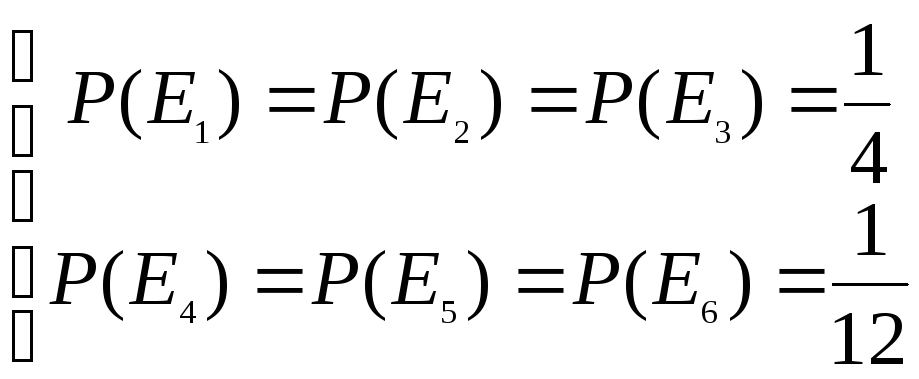(2)

Неполнота системы аксиом не является свидетельством их неудачного выбора, а вызвана существом дела. В различных задачах могут встретиться явления, при изучении которых требуется рассматривать одинаковые множества случайных событий, но с различными вероятностями. Например, в случае правильной игральной кости используется система вероятностей (1), а в случае неправильной кости, возможно, например, использование системы (2).