Критерий оптимальности базисного распределения поставок

Решение вопроса оптимальности базисного распределения разработан в гл. 5 (Исследования операц. в экономике) посвященный симплексному методу. Согласно ему в начале следует выразить линейную функцию задачи через не основные (свободные) переменные.

Транспортная задача – задача на минимум, поэтому оптимум достигнут тогда и только тогда когда все коэффициенты при свободных (не основных) переменных в выражении линейной функции неотрицательны. В транспортной задаче произвольная переменнаяотождествляется с содержимым соответствующей клетки (i,j) таблицы поставок. Коэффициентпри свободной переменнойв выражении линейной функцииFчерез свободные перемещенные называетсяоценкой свободной клетки (i,j).

Тогда критерий оптимальностиформулируется так: базисное распределение поставок оптимально тогда и только тогда, когда оценки всех свободных клеток неотрицательны.

Т. о. в первую очередь необходимо определить оценки свободных клеток для фиксированного базисного распределения поставок.

Пусть фиксировано некоторое базисное распределение поставок, при этом клетка (i,j) – свободная (переменная- свободная),- оценка клетки (i,j) или коэффициент прив выражении линейной функцииFчерез свободные переменные, т. е.:

(14)

где многоточием обозначены слагаемые, отвечающие свободным, переменным, отличным от ,- суммарные затраты на перевозку данного распределения поставок. Тогда из выражения (14) следует, что оценкасвободной клетки (i,j) равна приращению ∆Fсуммарных затрат на перевозку при переводе в клетку (i,j) единичной поставки (увеличение переменойот 0 до 1). Очевидно, что ∆F> 0, если> 0; ∆F< 0, если<0. Последнее косвенное определение оценки свободной клетки обычно называютэкономическим смыслом оценки свободной клетки.

Пример.Проверим на оптимальность первоначальное базисное распределение поставок методом наименьших затрат. Установить является ли оптимальным базисное распределение поставок найденное в задаче таб. 5 ( см. таб. 9).

Табл.9

	20		110		40		110
60	1		2		5		3
				60
120	1		6		5		2
		20						100
100	6		3		7		4
				50		40		10

Найдем, например, оценку свободной клетки (1,3). Для этого дадим (1,3) единичную поставку, при этом изменяем поставки в других, сохраняя баланс по строкам и столбцам. Будем полагать, что во всех свободных клетках, отличных от (1,3), поставка остается нулевой. Так чтобы третий потребитель получил по-прежнему сорок единиц груза, поставку в клетке (3,3) следует уменьшить на 1. Для того, чтобы поставщик отправил по-прежнему 100 единиц, поставку в клетке (3,2) увеличиваем на 1. Полученное распределение в табл. 10.

Табл.10

	20		110		40		110
60	1		2		5		3
				59		1
120	1		6		5		2
		20						100
100	6		3		7		4
				51		39		10

Найдем изменение ∆Fсуммарных затрат при указанном перераспределении поставок. Первоначальные затраты (табл. 9).

После перераспределения (табл. 10).

Учитывая экономический смысл оценки свободной клетки, получаем:

β₁₃= ∆F=F_n–Fн = 2 ∙ (-1) + 5 ∙ 1 + 3 ∙ 1 + 7 ∙ (-1) = -1

Т. к. среди клеток таблицы 9 есть клетка с отрицательной оценкой, то распределение поставок неоптимально.

Этот способ довольно громоздкий. Проанализируем решение задачи для укрощения вычислений.

При вычислении ∆Fмногие слагаемые изF_ПиF_Нвзаимно уничтожаются не влияя на значения ∆F:существеннылишь коэффициенты затрат тех клеток, в которых поставка при рассматриваемом перераспределении изменится. При этом в выравнивании для ∆Fнекоторые из них входят со знаком +, а некоторые со знаком -. Для удобства покажем это на рис. 1.

Рис. 1

На нем изображены клетки в которых будет изменена поставка. Знаком «+» обозначены клетки, в которых поставка увеличивается. Видно, что именно их коэффициент затрат войдут в выражение (15) для Fсо знаком «+». В остальных клетках рис.1 поставка уменьшится (в них знак «-»), их коэфф. затрат войдут в (15) дляFсо знаком «-«. Ломаное соединение клетки называется означенным циклом пересчета.

Т.о. привило 1 нахождение оценки свободной клетки звучит: для свободной клетки следует построить цикл пересчета в вершинах этого цикла расставить последовательно чередующие знаки, начина со знака «+» в свободной клетке, тогда значения оценки свободной клетки равно алгебраической сумме коэффициента затрат клеток цикла, взятых с соответствующими знаками. Аналогично находятся оценки каждой клетки.

Например, клетка (1,1)

	20		110		40		110
60	1	+	2	-	5		3
				60
120	1	-	6		5		2	+
		19						101
100	6		3	+	7		4	- -
				51		40		9

Оценка клетки:

Нахождение оценок свободных клеток можно упростить.

Теорема (о потенциалах). Оценка свободной клетки не изменяется, если к коэффициентам затрат некоторой строки (столбца) таблицы поставок прибавить некоторое число. Это число, прибавляемое к коэффициентам затрат выделенной строки (столбца), будем называть потенциалом данной строки(столбца).

Правило 2нахождение оценок сводных клеток: к коэффициентам затрат таблицы поставок в каждой строке и столбце надо прибавить такие числа (потенциалы), чтобы коэффициент затрат в заполненных клетках стали равными нулю. Полученные при этом коэффициенты затрат свободных клеток равны оценкам этих клеток.

Пример. Найти оценки свободных клеток базисного распределения поставок задачи- таблицы-5 .

Решение.Найдем оценки свободных клеток. Изменения коэффициентов затрат, можно начинать с любого столбца (строки). Потенциал строки ( столбца) избранного для начала, может быть произвольным, но можно доказать что после его фиксации потенциалы остальных столбцов(строк) будет определены однозначно. Начнем с1-го столбца. Пусть его потенциал равен 0. рядом с потенциалом в скобках записываем номер шага (поставки опускаем)

Табл.10

1		2		5		3	-2(7)
1		6		5		2	-1(2)
6		3		7		4	-3(4)
0(1)	0(6)		-4(5)			-1(3)

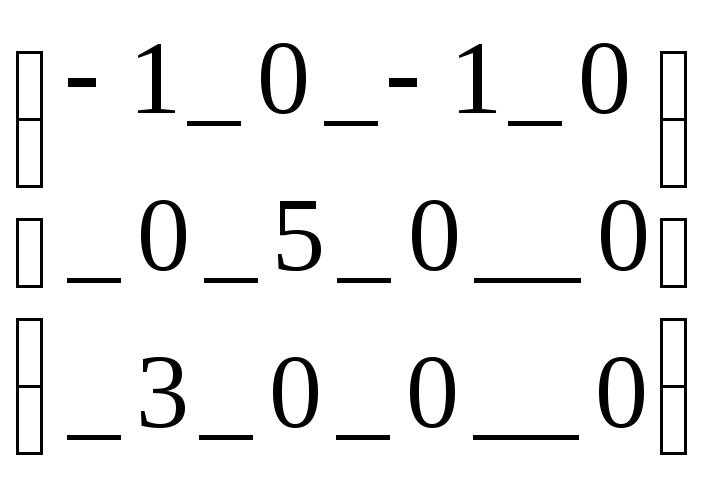(16)

После прибавления этого потенциала к коэффициентам затрат первого столбца коэффициент затрат заполненной клетки (2,1) не изменяется; чтобы полученный после сложения коэффициент стал равен 0, потенциал 2-ой строки таблице 10 должен быть равен -1; для обнуления коэффициента затрат (2,4) потенциала 4-го столбца должен быть равен -1 и т.д. Измененные коэффициенты затрат записываем в виде матицы(16).

Элементы матрицы оценок, соответствующие свободным клеткам таблицы поставок, равны оценкам этих свободных клеток.

Из предыдущих рассуждений вытекает, что для фиксированного базисного распределения поставок можно подобрать различные наборы поставщиков удовлетворяющих правилу 2, однако матрица оценок во всех случаях будет одинакова.

Распределительный метод решения транспортной задачи

Пример. Найти оптимальное распределение поставок задачи таблица 1.

Решение.Начнем с базисного распределения поставок полученного в задаче (таблица5). Как было установлено (см. задачу таблицу 10 и 15) данное распределение не оптимально. Учитывая результаты последней задачи (16) имеем

Значение найдено в задаче таблица 5. Далее поступаем так, как поступили бы, решая задачу симплексным методом: переменную, коэффициент при котором отрицателе, будем переводить в основные (базисные) переменные. Переменнаяначинает возрастать от нуля. Как было показано ранее, перевод поставки в свободную клетку вызывает перераспределение поставок (передвижение поставок по циклу). Означенный цикл пересчета для клетки(1,3) показан на рисунке 2.

Рис.2

Увеличиваем поставку в клетке(1,3), до тех пор пока поставка в одной из заполнены клеток не станет равной нулю. Эта клетка принадлежит циклу (рис2) для клетки (1,3). Если в клетку(1,3) передать поставку, равноZ, то по поставка в клетках цикла со знаком «+» увеличится наZ, а в клетках со знаком «-» уменьшится наZ. Поэтому искомая клетка находится среди клеток цикла имеющих знак «-». Более того, она имеет минимальную поставку среди таких клеток. Т.к. (рис2)то в нашем случае- это клетка(3,3), и для обнуления поставки в этой клетке по циклу следует передать 40 единиц, т.е поставка передаваемая по циклу, определяется как минимум среди поставок со знаком «-». После этого клетка(1,3) считается заполненной, а клетка(3,3) свободной,

Клетки со знаком «+» увеличивают на передаваемую поставку: клетка(3,2) равна 90 единиц, клетка(1,3) равна 40 единиц. Аналогично в клетках со знаком «-» поставка уменьшится на передаваемую поставку, например(1,2) станет равной 20 единиц. Вновь полученное распределение базисное (таблица 11).

1		2		5		3
			20		40
1		6		5		2
	20						100
6		3		7		4
			90				10

Табл.11

(6)-2

(2)-1

(4)-3

(1)0

(5)0

(7)-3

(3)-1

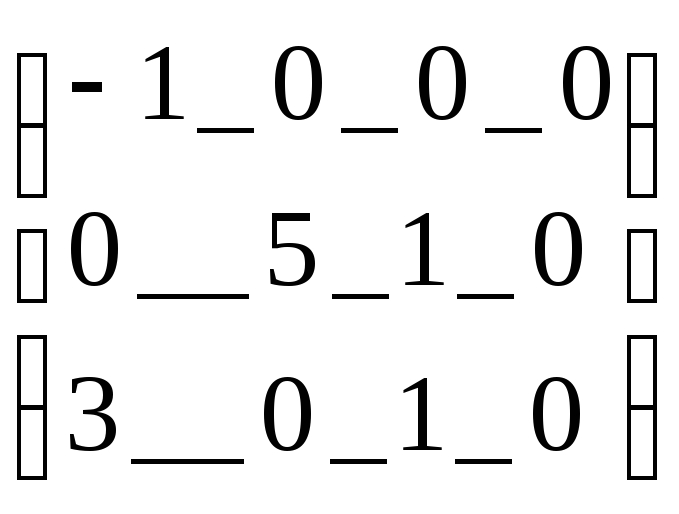(17)

! Возникает вопрос об оптимальности. Найдем оценки свободных клеток (матрицу оценок) распределение поставок. Для этого подберем потенциалы, так чтобы коэффициенты затрат заполненных клеток стали = 0. Тогда матрица оценок будет (17).

Т.к.(1,1) имеет отрицательную оценку, то найденное решение не оптимально и передача поставки в(1,1) ведет к уменьшению суммарных затрат на перевозку. Означенный цикл пересчета для(1,1) приведен на рисунке 3.

+

-

20

-

20

+

100

+

90

-

10

Рис.3

По правилу сформулированному выше, поставка, передаваемая по циклу . Передвигая эту поставку по циклу (рисунок 3), приходим к новому распределению поставок (таблица12).

1		2		5		3
	10		10		40
1		6		5		2
	10						110
6		3		7		4
			100

Табл.12

(18)

Найдя матрицу оценок (18) заключаем, что оно оптимально, т. к. среди оценок нет отрицательных. Суммарные затраты:

Экономия составит:

Знак минус означает, что суммарные затраты уменьшились.

Замечания

1. Поставка, предаваемая по циклу, не может быть, ни больше минимума поставок клеток со знаком «-»

2. Оптимальное распределение поставок найденное в задаче, не единственное, т.к. среди оценок свободных клеток есть нулевые.

Алгоритм решения закрытой транспортной задачи

1. Для данного базисного распределения поставок подберем потенциалы строк и столбцов таблицы поставок, так чтобы коэффициент затрат заполненных клеток стали равны нулю. Составляем матрицу оценок.

2. Если оценки всех свободных клеток не отрицательны, то найденное распределение оптимально - решение закончено. Если среди оценок свободных клеток есть отрицательные, то выберем одну из них для передачи в нее поставки (для определенности можно брать, например, одну из клеток с наименьшей оценкой.).

3. Для избранной свободной клетки строится означенный цикл пересчета. Поставка Z, передаваемая по циклу, определяется как минимум среди поставок в клетках со знаком -. Найденная поставка передвигается по циклу. При этом поставка в клетках цикла со знаком + увеличивается наz, а в клетках с – уменьшается наz. Клетка, поставка в которой при этом станет = 0 будет считаться свободной (далее рассмотрим случай, когда таких клеток несколько), остальные клетки цикла – заполненными. Т. о. получено новое базисное распределение поставок.

4 Переходим к п. 1 алгоритма.

Рассмотрим особые случаи, которые могут возникнуть при решении транспортной задачи.

1. В некоторых случаях поставка, переводимая по циклу, может оказаться = 0. Это возможно тогда, когда клетка цикла со знаком – содержала нулевую поставку. В этом случае по циклу передается нулевая поставка. В результате та свободная клетка, для которой был построен цикл, становится заполненной (нулевой поставкой), а клетка с нулевой поставкой – свободной.

2. Если при переводе поставки по циклу поставка обращается в нуль сразу в нескольких заполненных клетках, то свободной из них следует считать только одну (любую), остальные клетки, поставка в которых стала = 0, следует считать заполненными нулевой поставкой.

Разберем эти случаи на примере.

Задача.Завершить решение транспортной задачи таб. 6.

Табл.13

0	1		3		3
		20		10
0	3		3		2
				0		30
0	4		1		2
						10

Решение. Сначала установим оптимально ли распределение полученное методом «северо-западного» угла. Подберем потенциалы строк и столбцов, так чтобы коэффициент затрат заполненных клеток стали равны 0, матрица (19). Так как клетка (3,2) отрицательна, распределение не оптимально.

матр.19

Переведем поставку в клетку (3,2) с отрицательной оценкой. Построим для (3,2) цикл пересчета, находим, что объем передаваемой поставки равен x_3.2=min(0.10)=0. Передавая по построенному циклу нулевую поставку, приходим к новому базисному распределению (табл.14). Подбирая потенциалы к строкам и столбцам табл. 14 находим матрицу оценок распределения (20).

Т. к. (1,3) отрицательна то данное базисное распределение не оптимально. Найдем новое базисное распределение передавая постановку в (1,3) с отрицательной оценкой. Построим цикл для (1,3).

Табл. 14

1		3	-	3	+
	20		10
3		3		2
					30
4		1	+	2	-
1			0		10

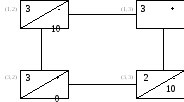
-2

0

0

-1

-2

(20)

Поставка, передаваемая в клетку(1,3):. При передачи по циклу 10 единиц груза станут равными нулю поставки в клетках (1,2) и (3,3). Только одна из них стала свободной напр.(3,3), а (1,2) заполнена нулевой поставкой т.о. получим базисное распред. поставок таблица 15.

1		3		3	-1
	20		0		10
3		3		2	0
					30
4		1		2	1
			10

(21)

-2

-2

0

0

Определим матрицу поставок. Среди оценок свободных клеток найденного распределения нет отрицательных т.с. найденное распред.(таблица 15) оптимально.