РГЗ_4задачи_решение_7вариант

Вариант 7

Задача 1

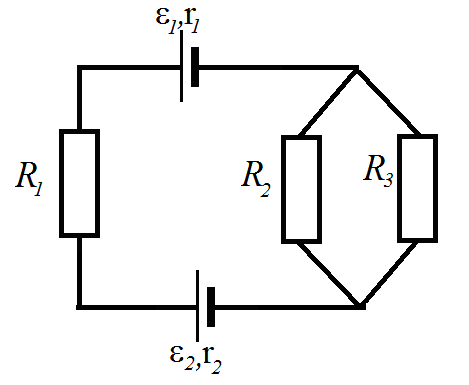
На рис. 16 изображен участок электрической цепи. Определить:

1) силу тока;

2) разность потенциалов между точками С и К.

Данные для варианта 7взяты из табл. 2.

Дано

Рис. 16

1. Определение силы тока

Закон Ома для неоднородного участка цепи, на котором помимо электростатических сил действуют еще и сторонние силы, имеет вид:

,

где – разность потенциалов на участке цепи, – ЭДС источников тока, – полное сопротивление внешней цепи, – внутренние сопротивления источников тока. ЭДС учитываются с положительным знаком, если при обходе приходится идти от минуса к плюсу внутри источника тока.

Определим полное сопротивление внешней цепи.

При последовательном соединении проводников их общее сопротивление равно сумме сопротивлений, поэтому

.

Тогда выражение для силы тока примет вид:

.

Вычисления:

.

2) Определение разности потенциалов между точками Д и В

Воспользуемся опять законом Ома для неоднородного участка цени, записав его для участка Д В, учтя при этом, что на этом участке имеется только источник тока и резисторы и :

,

откуда выражаем разность потенциалов

.

Вычисления:

.

Ответ: ,

Задача 2

Дан участок электрической цепи ( рис. 19). Определить заряд, протекающий по цепи за промежуток времени от до , если один из параметров цепи меняется со временем.

Данные для варианта 7 взяты в табл. 4.

Дано

Рис. 19

1) Связь заряда, протекающего по цепи, с силой тока в ней

Сила тока по определению равна

,

откуда заряд, прошедший по цепи, можно найти интегрированием по времени в пределах от до :

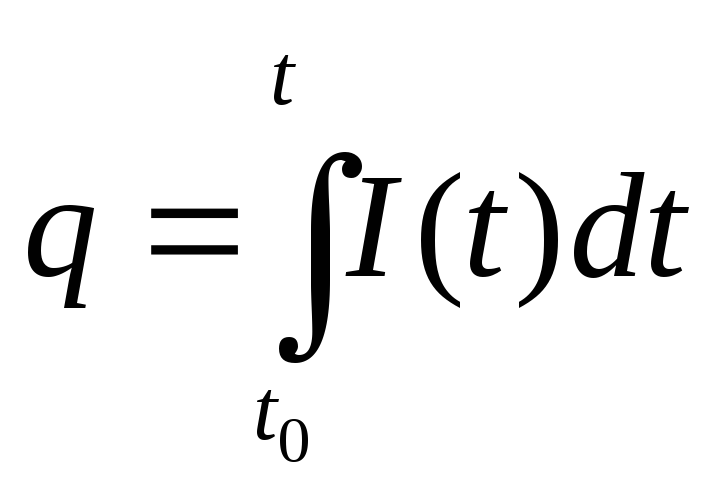. (1)

Найдем силу тока в контуре как функцию времени

.

2) Определение силы тока

Общий ток в контуре можно определить по закону Ома для замкнутой цепи. С учетом того, что в контуре два источника тока и , включенных последовательно навстречу, запишем закон Ома в следующем виде:

, (2)

где – полное сопротивление внешней цепи, – внутренние сопротивления источников тока.

Определим полное сопротивление внешней цепи.

Для начала учтем, что резисторы и соединены параллельно, а при параллельном соединении проводников справедлива формула

,

откуда находим

,

где – общее сопротивление резисторов и .

Далее используем формулу последовательного соединения и получаем:

или . (3)

После подстановки (3) в (2) получим:

.

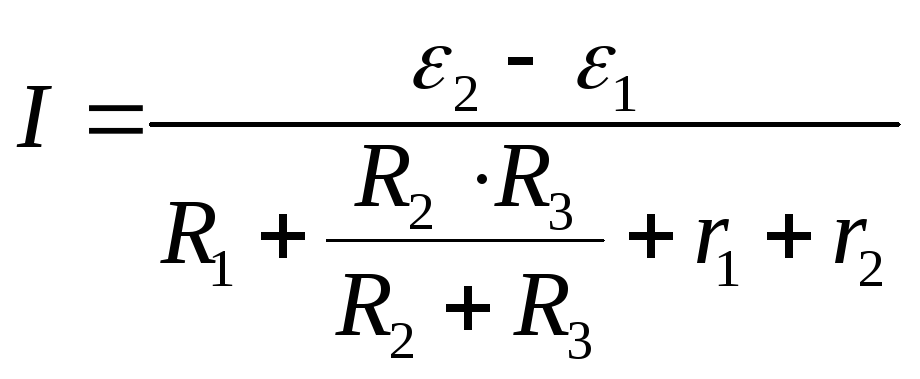Найдем выражения зависимости силы тока от времени в виде уравнения с числовыми коэффициентами:

3) Вычисление заряда

Подставим это выражение под знак интеграла в (1) и проинтегрируем:

.

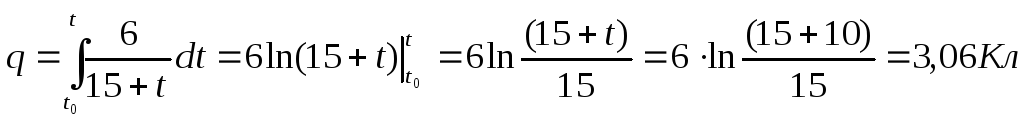Ответ:

Задача 3

Провод в виде части окружности радиусом находится в однородном магнитном поле с индукцией , . По проводу течет ток силой . Найти силу, действующую на провод, если он лежит в плоскости, перпендикулярной линиям индукции.

Данные для варианта 7 взяты в табл. 13.

Дано

Решение

Формула для силы Ампера в виде справедлива только в случае прямолинейного проводника длиной с током длиной , находящегося в однородном поле с индукцией длиной , - угол между направлением тока в проводнике и направлением силовых линий поля.

В случае проводника произвольной формы разбиваем его на столь малые участки, чтобы каждый из них можно было считать элементом тока. Рассмотрим один такой участок, длина которого . Для него угол между направлением вектора магнитной индукции и элементом тока равен , поэтому модуль вектора элементарной силы, действующей на этот участок, по закону Ампера имеет вид:

.

Если линии индукции направлены перпендикулярно плоскости полукольца, элементарные векторы направлены (по правилу левой руки) в плоскости кольца перпендикулярно элементу тока .

Проведем ось вдоль диаметра контура так, чтобы он был симметричен относительно нее, и разобъем контур на отдельные участки, как показано на рисунке. В силу приведенных выше рассуждений можно утверждать, что благодаря симметрии силы, действующие на участки и , равны по величине и противоположны по направлению, то есть компенсируют друг друга. Тогда действующая на весь проводник сила будет равна силе, действующей на участок четверти кольца . Рассчитаем ее.

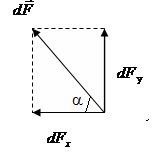
Разложим вектор силы, действующей на элемент кольца, на две составляющие - и . В силу симметрии полукольца относительно вертикальной оси

Тогда результирующая сила определится выражением:

.

Представим, тогда

.

Вынесем постоянные члены за знак интеграла и проинтегрируем по углу, учтия при этом, что для участка он изменяется в пределах от до :

.

Проверка размерности:

Вычисления:

Ответ:

Задача 4

По катушке из тонкой проволоки течет ток . Площадь поперечного сечения катушки , число витков в ней . Катушка помещена однородное магнитное поле с индукцией , . Определить магнитный момент катушки и вращающий момент , действующий на нее со стороны поля, если ось катушки составляет угол с линиями индукции.

Данные для варианта 7 взяты в табл. 9.

Дано

Решение

1) Магнитный момент

Магнитный момент витков с током определяется по формуле:

,

где - сила тока,

- площадь сечения контура.

- единичная положительная нормаль к контуру.

В скалярном виде выражение для магнитного момента

.

Проверка размерности:

.

Вычисления:

Направление связано с направлением тока в контуре правилом правого винта.

2) Вращающий момент

Вращающий момент , который действует на контур с током в магнитном поле с индукцией :

,

или в скалярном виде

,

где - магнитный момент рамки с током, вектор которого направлен по нормали к контуру,

- угол между векторами и , или угол между нормалью к контуру и силовыми линиями поля.

Проверка размерности:

Воспользуемся определенным ранее значением магнитного момента и вычислим

,

то есть при таком положении катушки, когда вектор магнитной индукции и магнитный момент лежат на одной прямой, вращающий момент не создается.

Ответ: ,