- •Государственное общеобразовательное учреждение высшего профессионального образования
- •Содержание
- •Периодичность функций
- •Простейшие преобразования графиков
- •Решение типового варианта
- •2. Предел последовательности. Предел функции. Теоремы о пределах
- •Решение типового варианта
- •3. Замечательные пределы
- •Решение типового варианта
- •4. Сравнение и эквивалентность бесконечно малых функций Бесконечно малая функция
- •Решение типового варианта
- •5. Односторонние пределы. Непрерывность функций
- •Решение типового варианта
Решение типового варианта
1.
![]() .
.
Воспользуемся первым замечательным пределом (3) предварительно сведя к нему исходное выражение
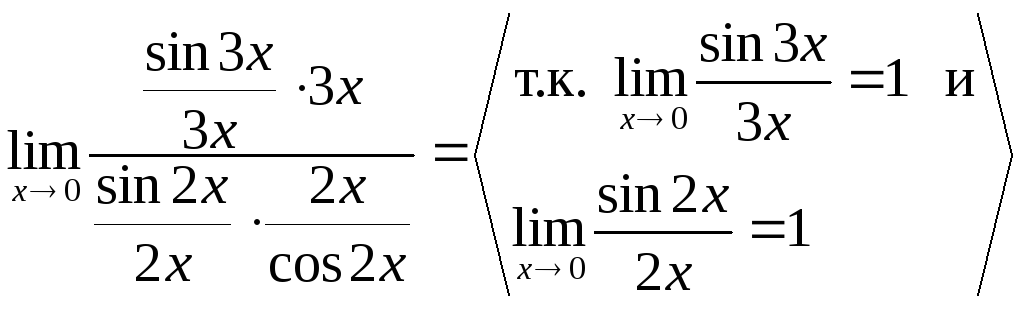 =
=![]()
2.
![]()
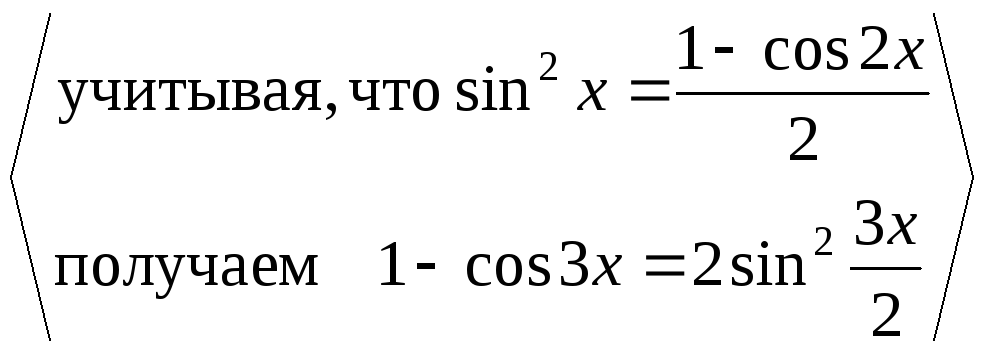 =
=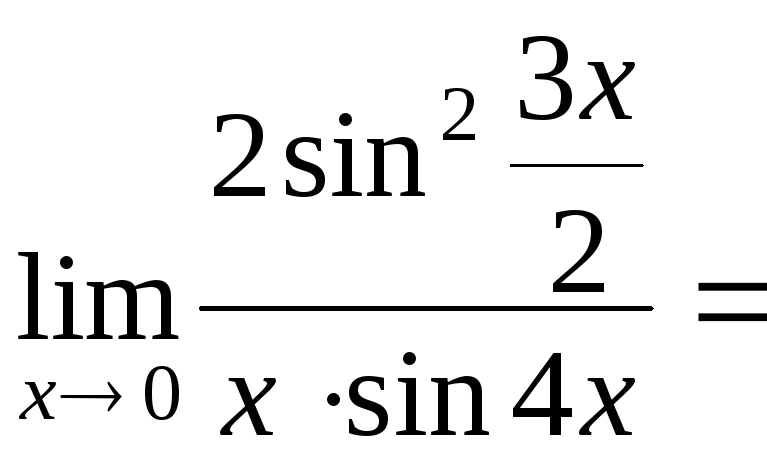
=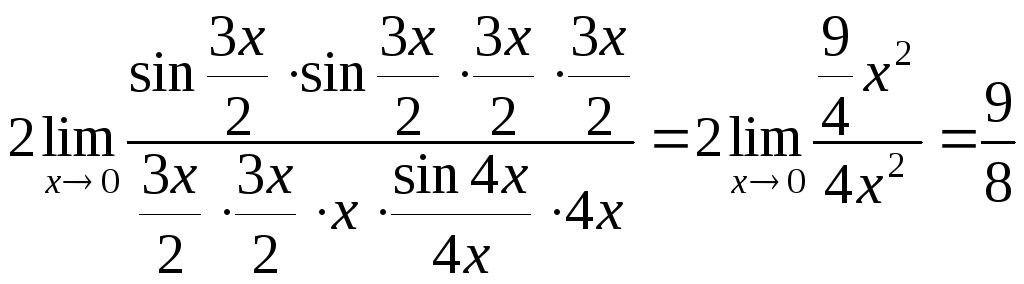 .
.
3.
![]() ,
,
![]() .
.
4.
![]() .
.
Сведем исходный предел ко второму замечательному пределу (4)

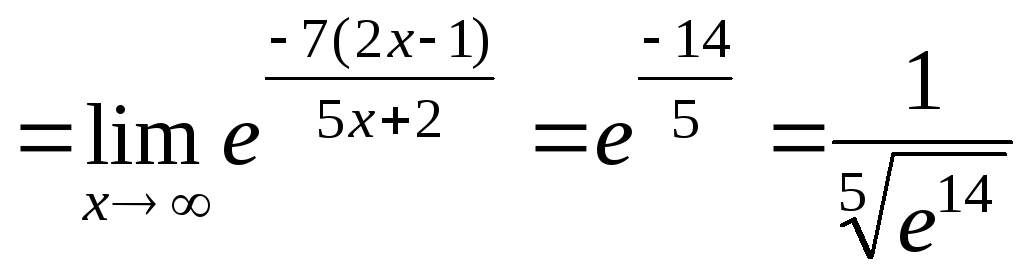 .
.
5.
![]() .
.
Воспользуемся другой формой записи второго замечательного предела (4’).
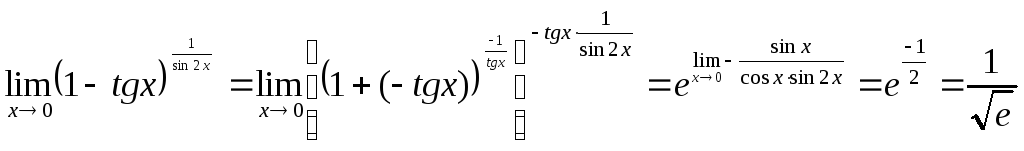 .
.
4. Сравнение и эквивалентность бесконечно малых функций Бесконечно малая функция
Определение.
Если
![]() (т.е. для любого
(т.е. для любого![]() существует
существует![]() ,
такое, что при
,
такое, что при![]() справедливо неравенство
справедливо неравенство![]() )
то
)
то![]() называетсябесконечно
малой функцией
при
называетсябесконечно
малой функцией
при
![]() .
Для сравнения двух бесконечно малых
.
Для сравнения двух бесконечно малых![]() и
и![]() при
при![]() находят предел их отношения
находят предел их отношения
![]() . (5)
. (5)
если
![]() ,
то
,
то![]() - бесконечно малая более высокого
порядка, чем
- бесконечно малая более высокого
порядка, чем![]() ;
;
если
![]() ,
то
,
то![]() - бесконечно малая более низкого порядка,
чем
- бесконечно малая более низкого порядка,
чем![]() ;
;
если
![]() ,
то
,
то![]() и
и![]() - бесконечно малые одного порядка;
- бесконечно малые одного порядка;
если
![]() ,
то
,
то![]() и
и![]() называютсяэквивалентными
величинами:
называютсяэквивалентными
величинами:
![]() ~
~![]() .
.
Примеры
эквивалентных б.м.в (при
![]() )
)
![]() ~
~
![]()
![]() ~
~
![]()
![]() ~
~
![]()
![]() ~
~
![]()
![]() ~
~
![]()
![]() ~
~
![]()
![]() ~
~
![]()
![]() ~
~
![]()
![]() ~
~
![]()
Для
раскрытия неопределенности вида
![]() можно воспользоваться следующим
правилом: если
можно воспользоваться следующим
правилом: если![]() ~
~![]() ;
;![]() ~
~![]() при
при![]() то верны равенства:
то верны равенства:
![]()
АЗ-4
1.
Сравнить функции
![]() и
и![]() при
при![]()
а)
![]() ,
,![]() ; б)
; б)![]() ,
,![]() ;
;
в)
![]() ,
,![]() ; г)
; г)![]() ,
,![]() .
.
2.
Доказать, что функцию
![]() и
и![]() при
при![]() является бесконечно малыми одного
порядка.
является бесконечно малыми одного
порядка.
![]()
![]() данные
функции одного порядка малости ч.т.д.
данные
функции одного порядка малости ч.т.д.
3. Найти пределы, используя эквивалентные бесконечно малые функции.
а)
![]()
![]() б)
б)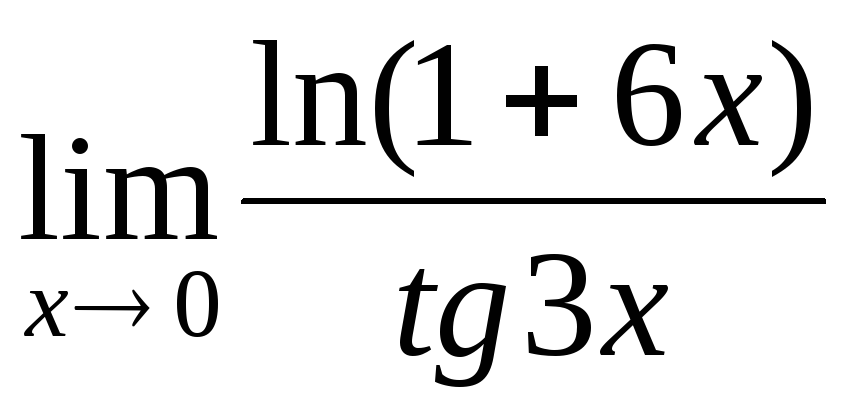
![]()
в)
![]()
![]() г)
г)![]()
![]()
д)
![]()
![]() е)
е)![]()
![]()
ж)
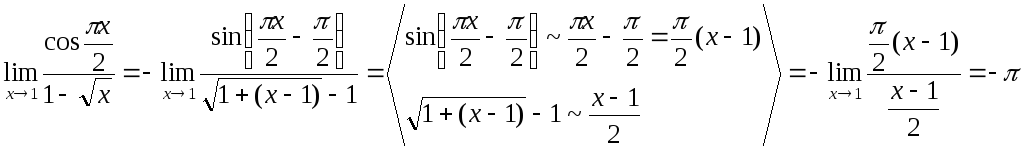
ИДЗ-4
Задание
1. Сравнить
бесконечно малые функции
![]() и
и![]() при
при![]()
|
№ вар |
|
|
№ вар |
|
|
|
1. |
|
|
16. |
|
|
|
2. |
|
|
17. |
|
|
|
3. |
|
|
18. |
|
|
|
4. |
|
|
19. |
|
|
|
5. |
|
|
20. |
|
|
|
6. |
|
|
21. |
|
|
|
7. |
|
|
22. |
|
|
|
8. |
|
|
23. |
|
|
|
9. |
|
|
24. |
|
|
|
10. |
|
|
25. |
|
|
|
11. |
|
|
26. |
|
|
|
12. |
|
|
27. |
|
|
|
13. |
|
|
28. |
|
|
|
14. |
|
|
29. |
|
|
|
15. |
|
|
30. |
|
|
Задание 2. Найти пределы, используя эквивалентные бесконечно малые
|
1. |
|
11. |
|
21. |
|
|
2. |
|
12. |
|
22. |
|
|
3. |
|
13. |
|
23. |
|
|
4. |
|
14. |
|
24. |
|
|
5. |
|
15. |
|
25. |
|
|
6. |
|
16. |
|
26. |
|
|
7. |
|
17. |
|
27. |
|
|
8. |
|
18. |
|
28. |
|
|
9. |
|
19. |
|
29. |
|
|
10. |
|
20. |
|
30. |
|
Задание 3.* Вычислить пределы функций
|
1.
|
11.
|
21.
|
|
2.
|
12.
|
22.
|
|
3.
|
13.
|
23.
|
|
4.
|
14.
|
24.
|
|
5.
|
15.
|
25.
|
|
6.
|
16.
|
26.
|
|
7.
|
17.
|
27.
|
|
8.
|
18.
|
28.
|
|
9.
|
19.
|
29.
|
|
10.
|
20.
|
30.
|
Решение типового варианта
Задание 1. Сравнить бесконечно малые функции
![]() и
и
![]() при
при![]()
Решение. Находим
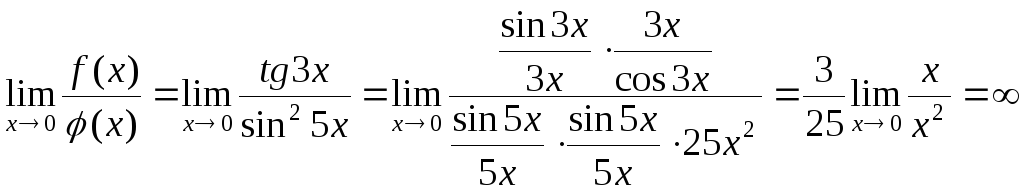
![]()
![]() -
бесконечно малая более низкого порядка
по сравнению с
-
бесконечно малая более низкого порядка
по сравнению с
![]() .
.
Задание 2. Найти пределы, используя эквивалентность бесконечно малых
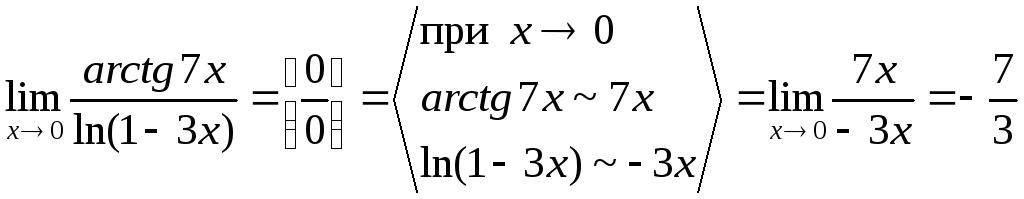
Задание 3. Вычислить предел функции
а)
![]()
Запишем
![]() как
как![]() и перейдем к эквивалентной бесконечно
малой
и перейдем к эквивалентной бесконечно
малой![]() ~
~![]() ,
получаем
,
получаем
![]() .
.
б)
![]()
Запишем
![]() как
как![]() ~
~![]()
![]() как
как![]() ~
~![]() ,
получим
,
получим
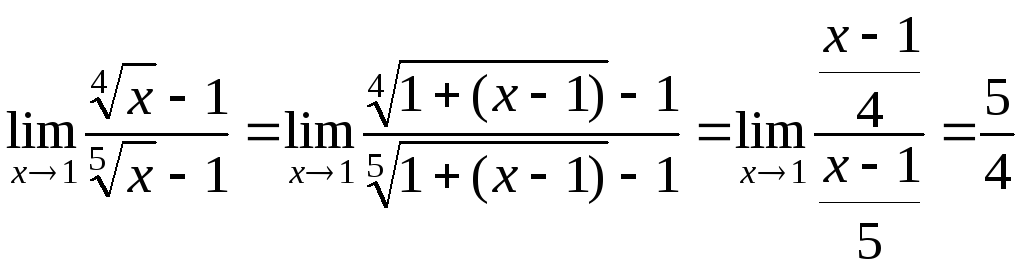 .
.