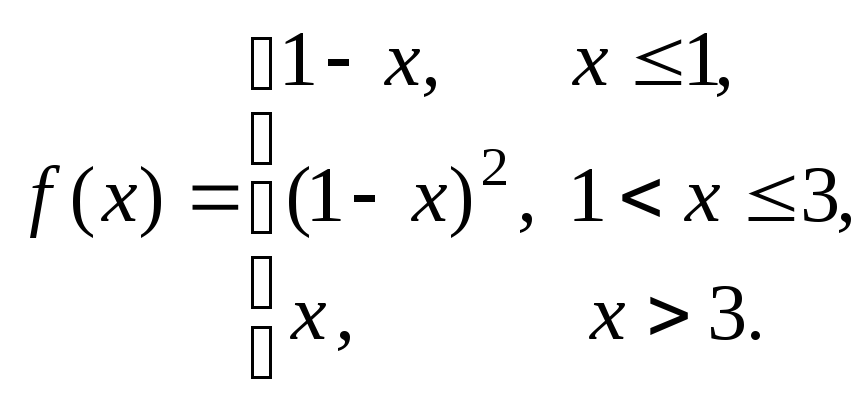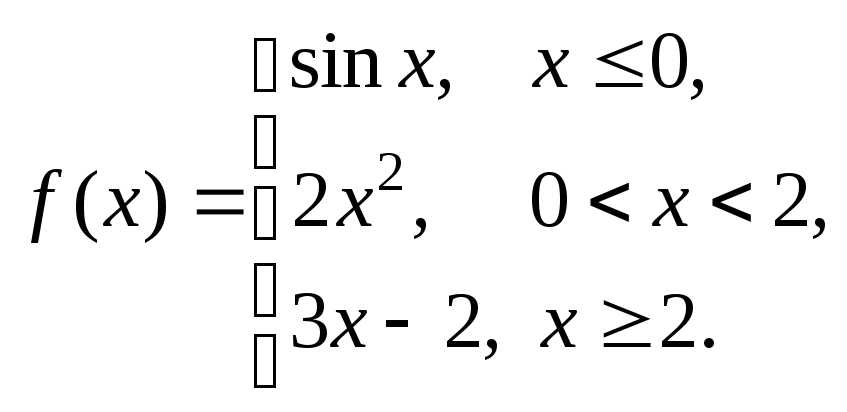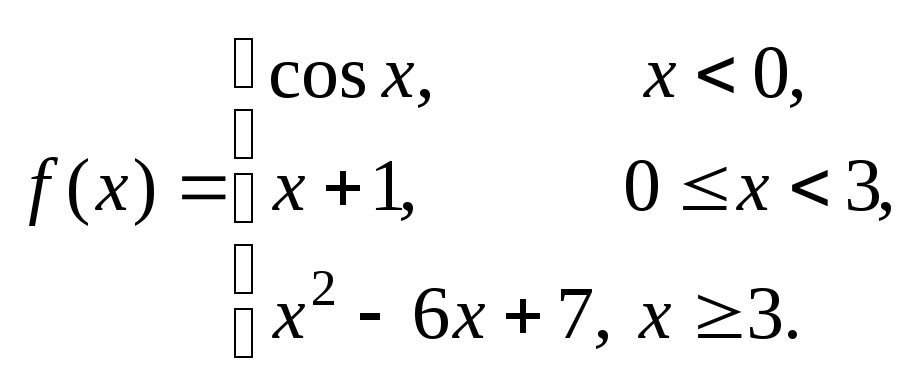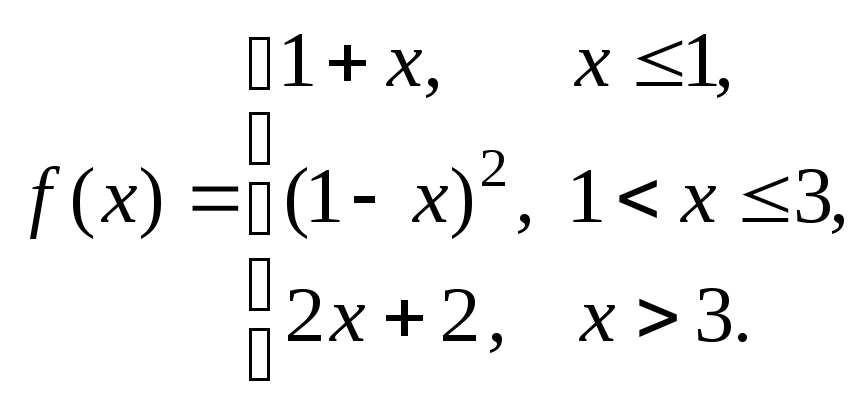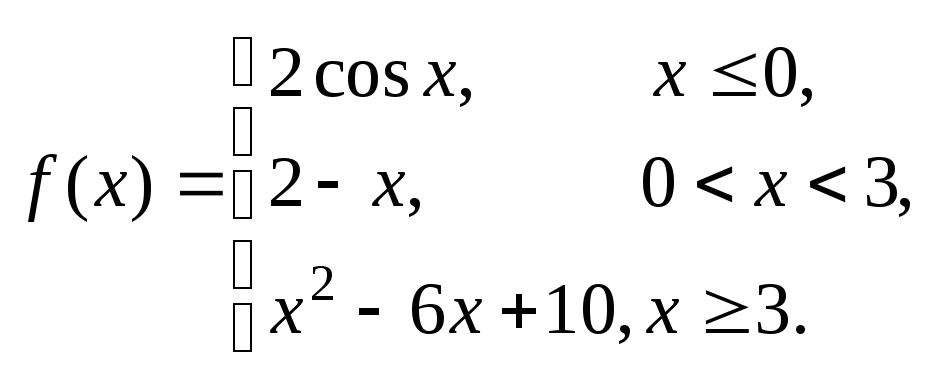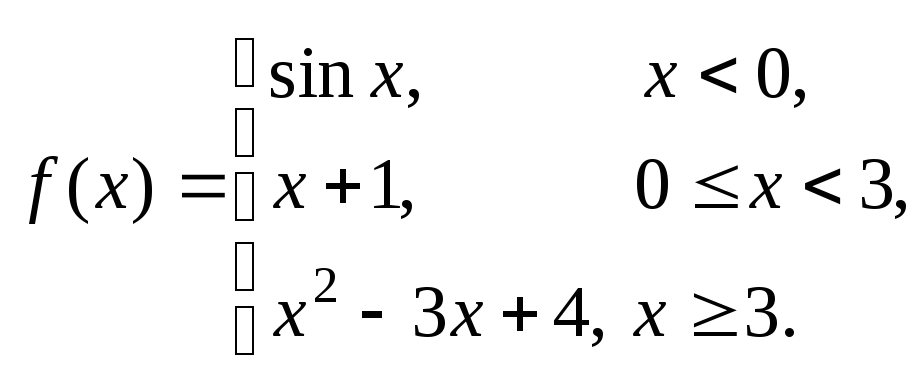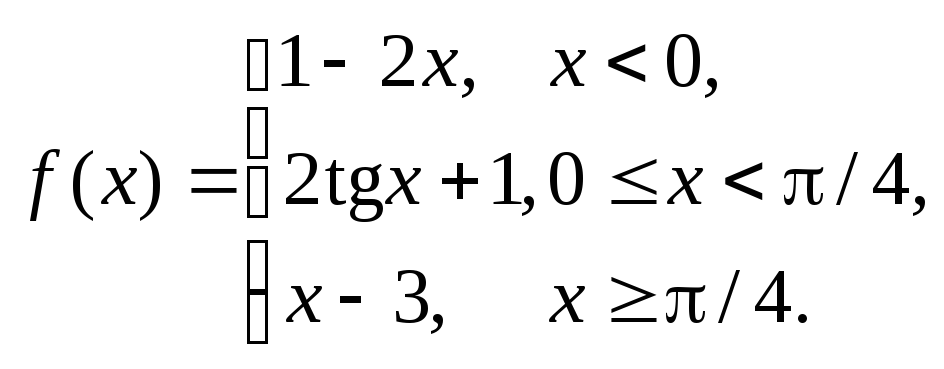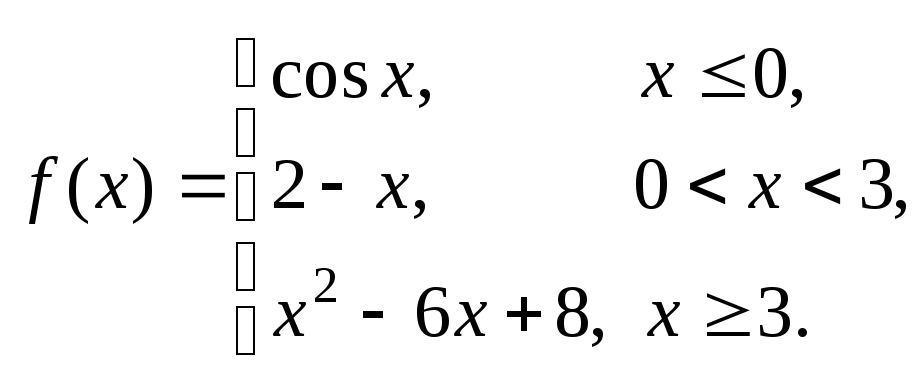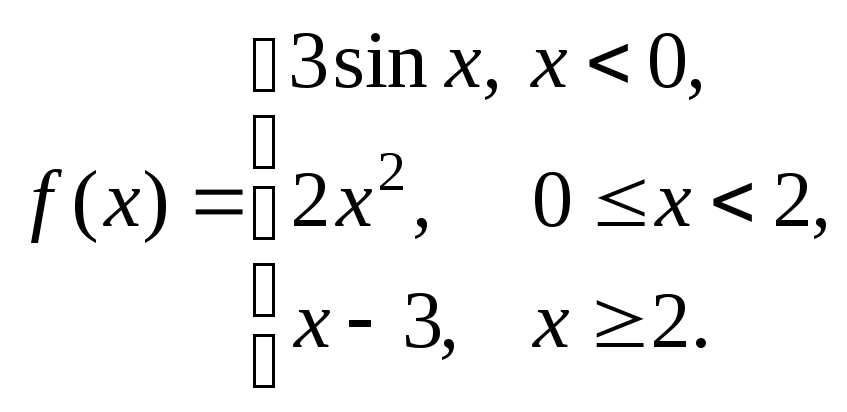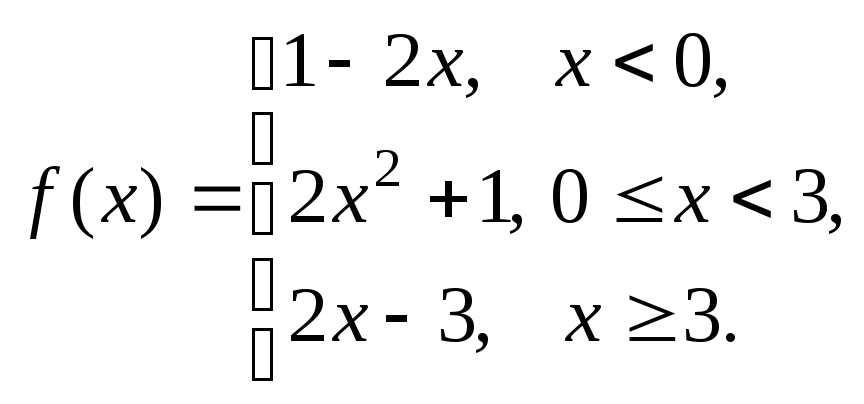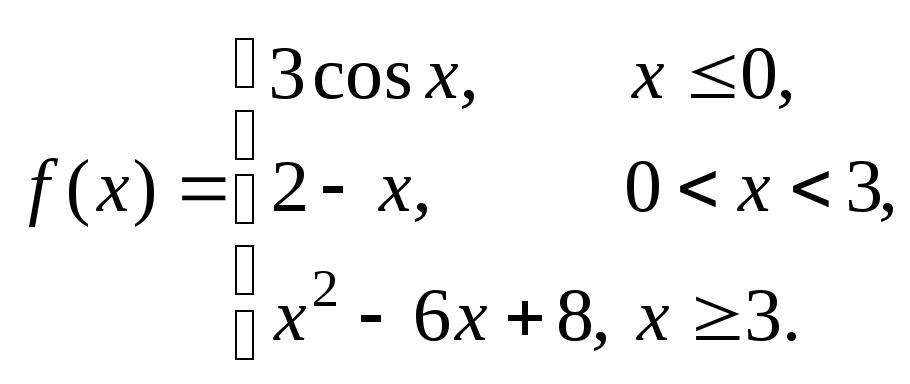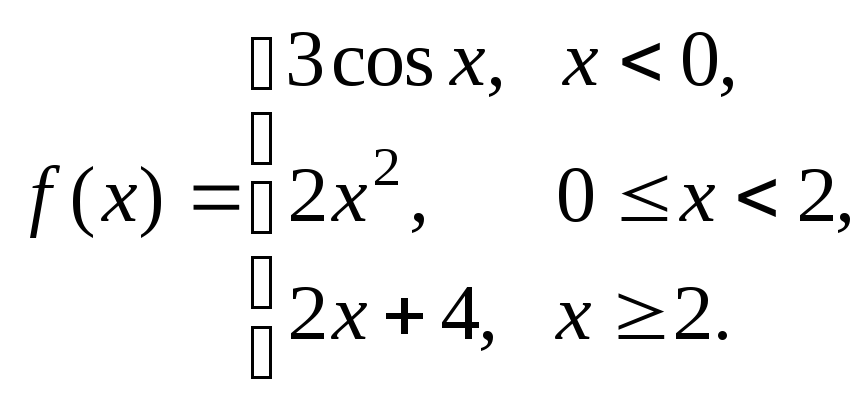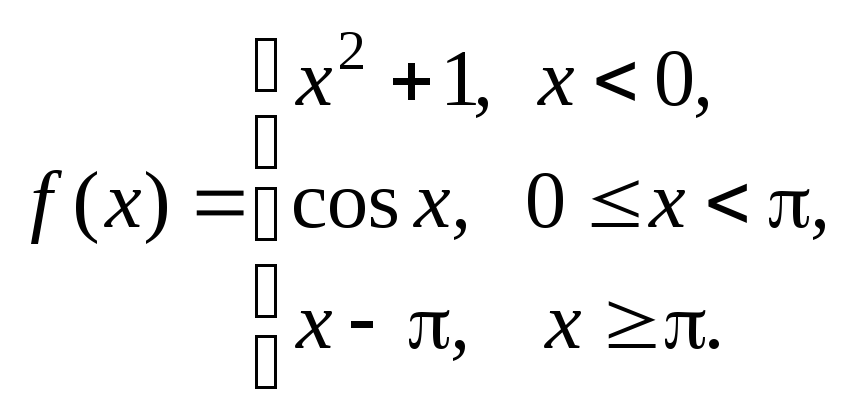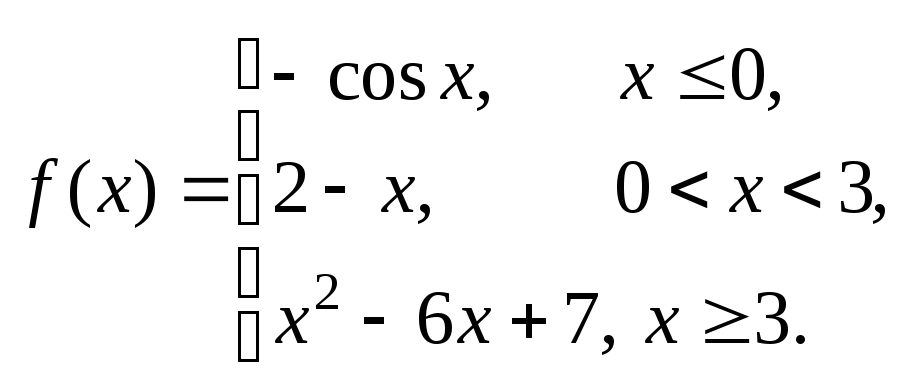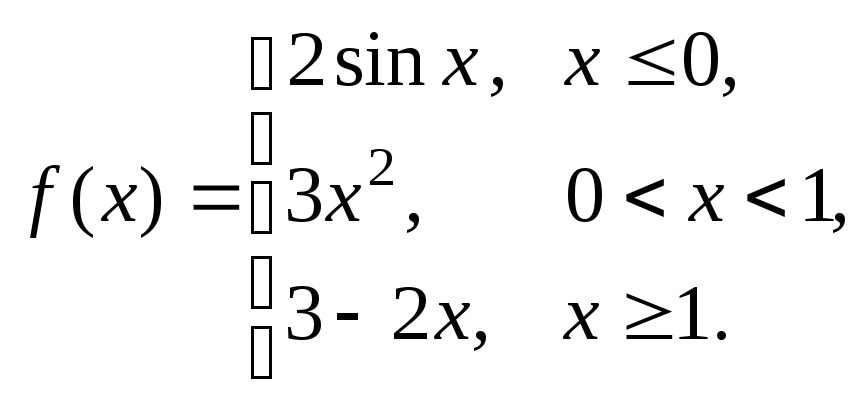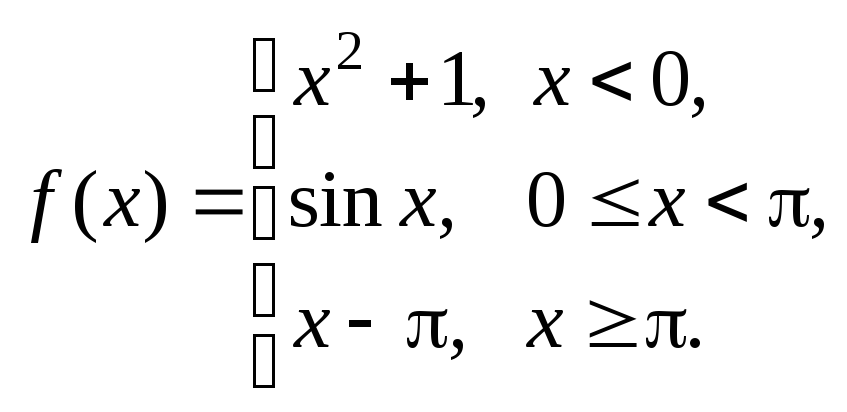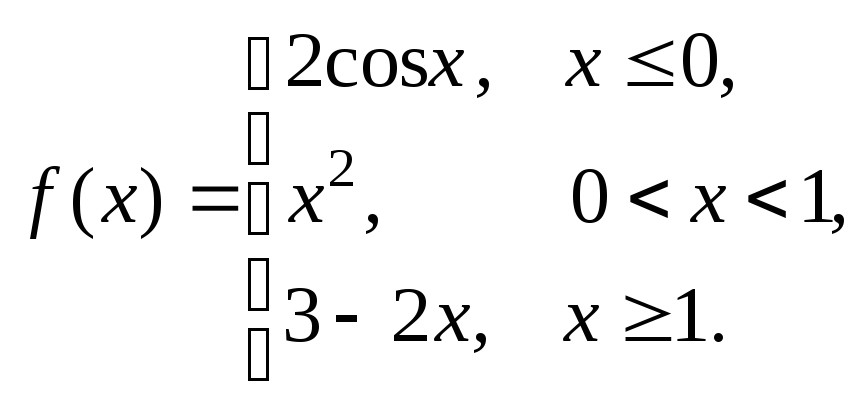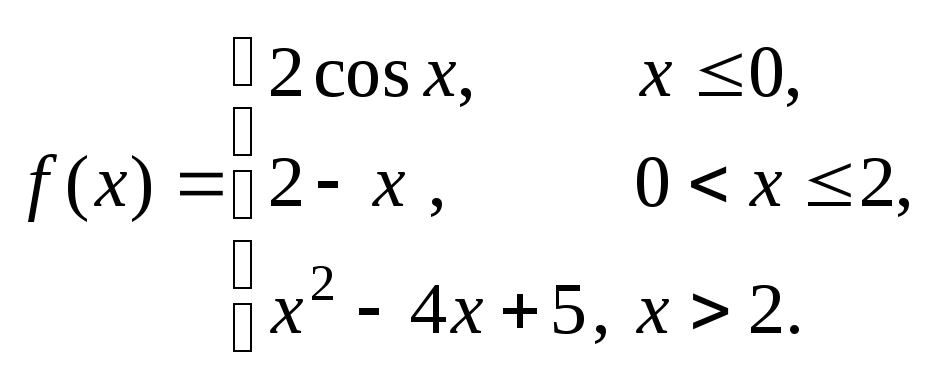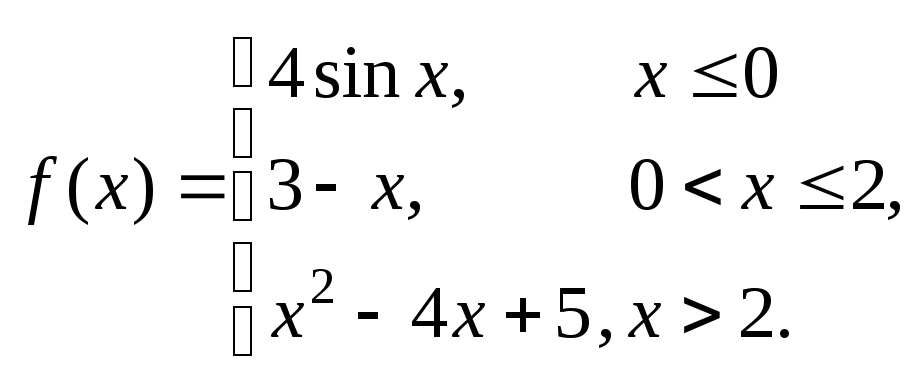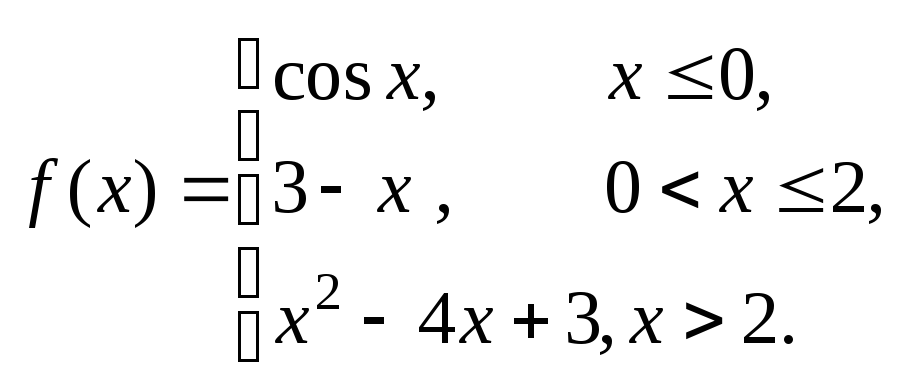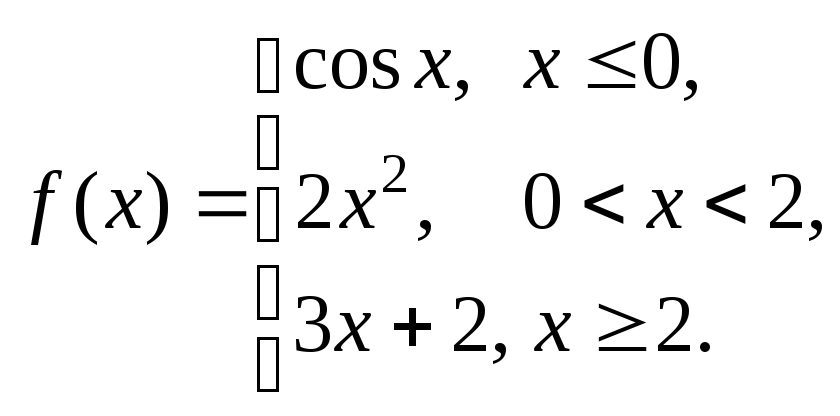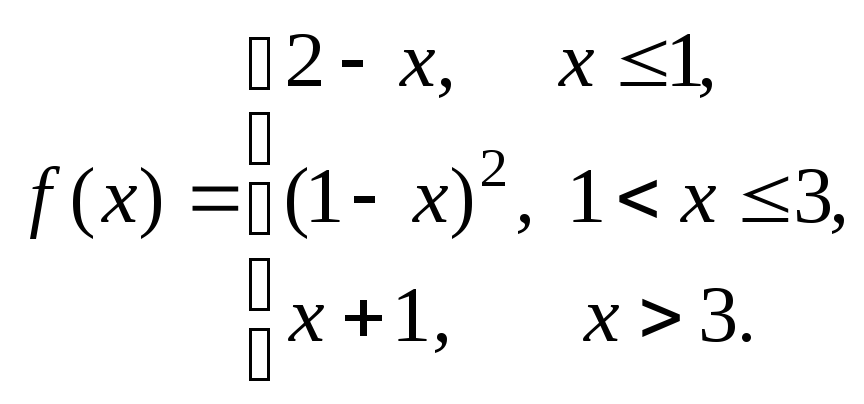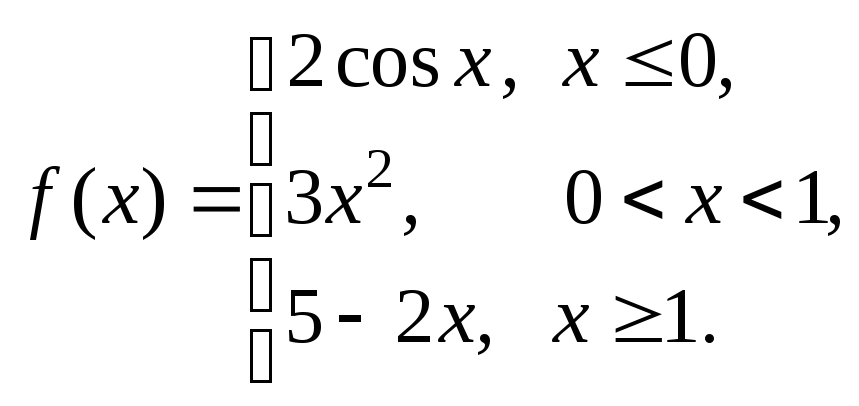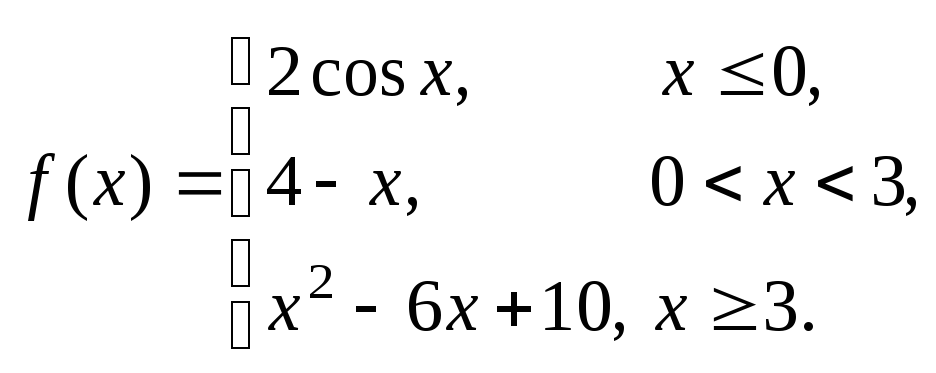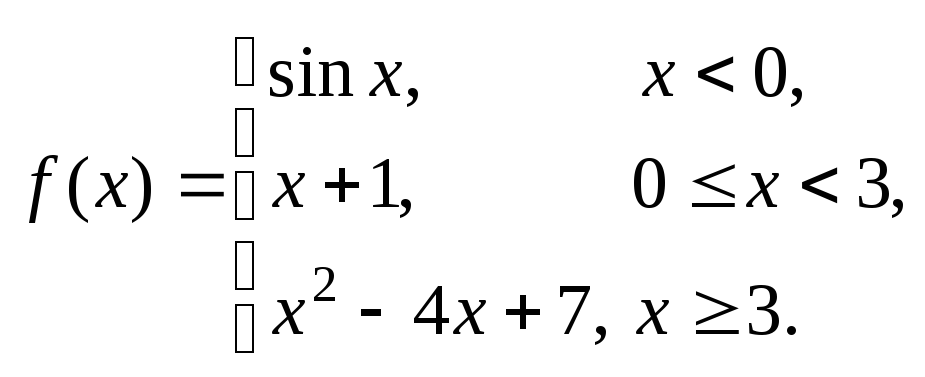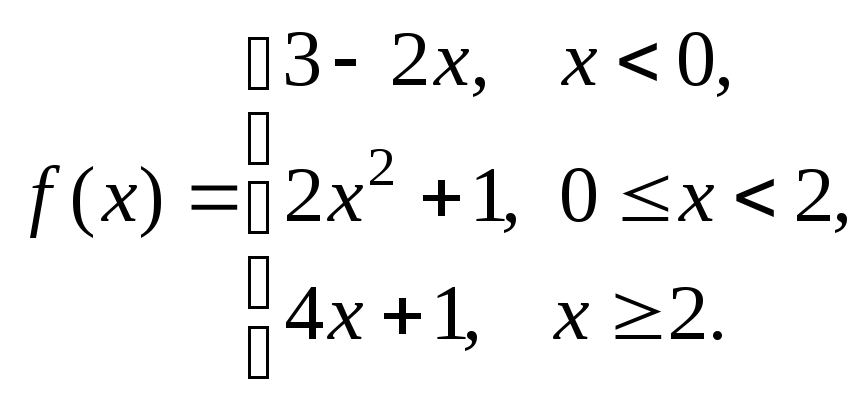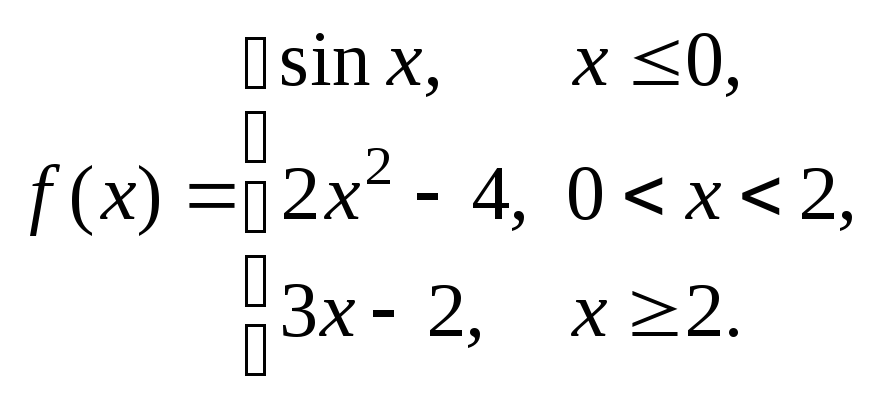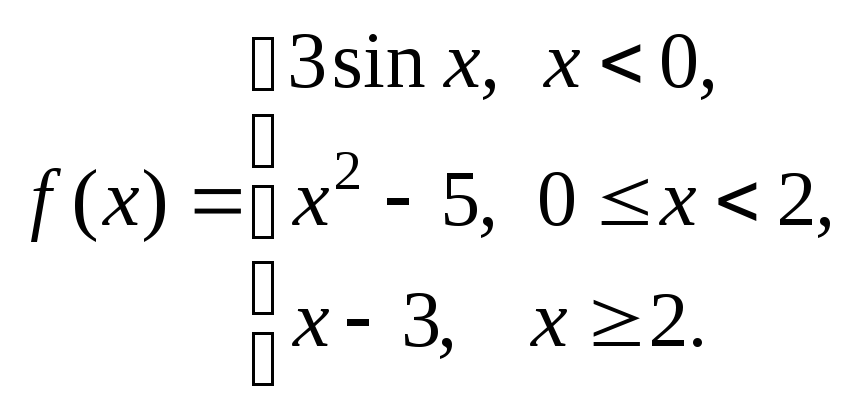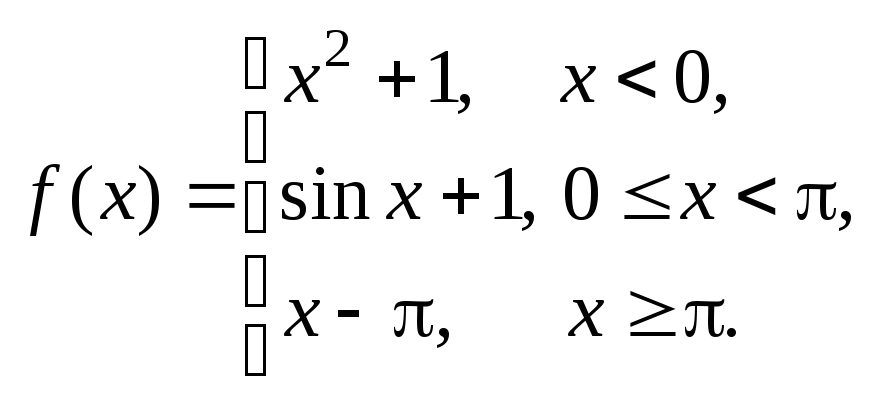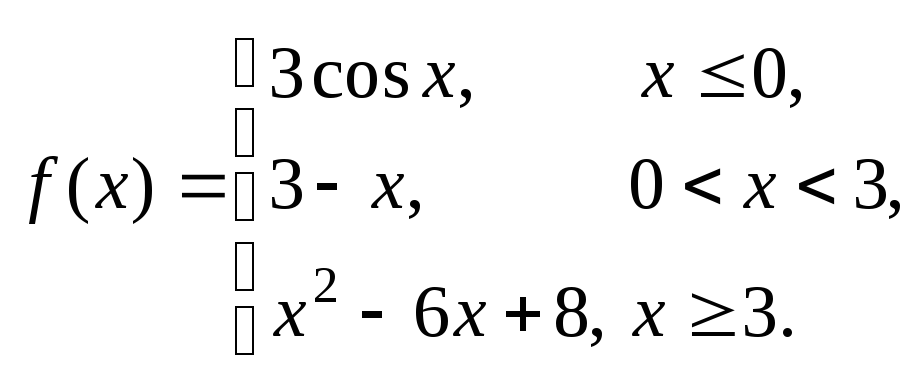- •1. Задания для контрольной работы №1 Задание № 1
- •Задание № 2
- •Задание № 3
- •Задание № 4
- •Задание № 5
- •2. Решение типового варианта кр № 1
- •3. Задания для контрольной работы № 2 Задание № 6
- •Задание № 7
- •Задание № 8
- •Задание № 9
- •4. Решение типового варианта кр № 2
- • Рекомендуемая литература
- •Оглавление
3. Задания для контрольной работы № 2 Задание № 6
Даны комплексные числа z1иz2(таблица 5).
а). Записать их в тригонометрической
форме и отметить полученные числа на
комплексной плоскости;б). Найти
числаz1 +z2,z1 –z2,
построить;в). Найти z1
z2,z1
/z2, записать
в тригонометрической и алгебраической
формах, сравнить результаты;г).
Найти![]() ;д). Найти
;д). Найти![]() ,
построить.
,
построить.
Таблица 5
|
№ варианта |
z1 |
z2 |
№ варианта |
z1 |
z2 |
|
6.1. |
|
|
6.16. |
|
|
|
6.2. |
3 + 3i |
|
6.17 |
– 4 + 4i |
|
|
6.3. |
|
|
6.18. |
|
|
|
6.4. |
|
|
6.19. |
|
|
|
6.5. |
– 2 + 2i |
|
6.20. |
3 – 3i |
|
|
6.6. |
|
|
6.21. |
|
|
|
6.7 |
|
|
6.22. |
|
|
|
6.8. |
– 4 – 4i |
|
6.23. |
2 – 2i |
|
|
6.9. |
|
|
6.24. |
|
|
|
6.10. |
|
|
6.25. |
|
|
|
6.11. |
1 – i |
|
6.26. |
1 + i |
|
|
6.12. |
|
|
6.27 |
|
|
|
6.13. |
|
|
6.28. |
|
|
|
6.14. |
2 + 2i |
|
6.29. |
– 5 + 5i |
|
|
6.15. |
|
|
6.30. |
|
|
Задание № 7
Найти пределы функций.
7.1.а)![]() при
при![]() ,
,![]() ,
,![]() ;
;
б)![]() ;в)
;в)![]() ;г)
;г)![]() .
.
7.2.а)![]() при
при![]() ,
,![]() ,
,![]() ;
;
б)![]() ;в)
;в)![]() ;г)
;г)![]() .
.
7.3.а)![]() при
при![]() ,
,![]() ,
,![]() ;
;
б)![]() ;в)
;в)![]() ;г)
;г)![]() .
.
7.4.а)![]() при
при![]() ,
,![]() ,
,![]() ;
;
б)![]() ;в)
;в)![]() ;г)
;г)![]() .
.
7.5.а)![]() при
при![]() ,
,![]() ,
,![]() ;
;
б)![]() ;в)
;в)![]() ;г)
;г)![]()
7.6.а)![]() при
при![]() ,
,![]() ,
,![]() ;
;
б)![]() ;в)
;в)![]() ;г)
;г)![]() .
.
7.7.а)![]() при
при![]() ,
,![]() ,
,![]() ;
;
б)![]() ;в)
;в)![]() ;г)
;г)![]() .
.
7.8.а)![]() при
при![]() ,
,![]() ,
,![]() ;
;
б)![]() ;в)
;в)![]() ;г)
;г)![]() .
.
7.9.а)![]() при
при![]() ,
,![]() ,
,![]() ;
;
б)![]() ;
в)
;
в)![]() ;г)
;г)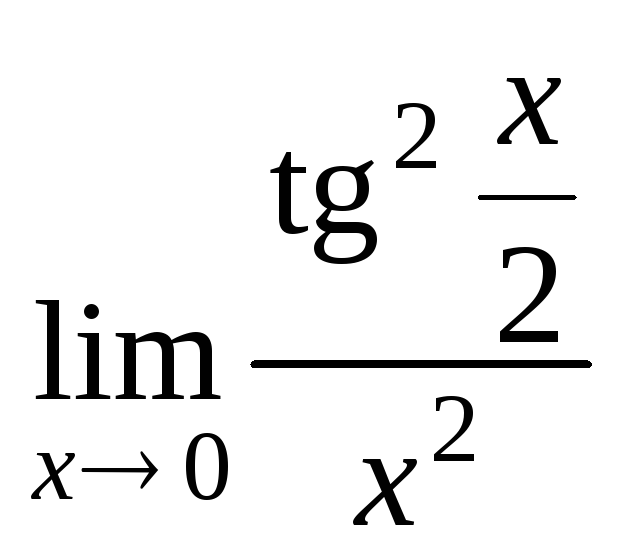 .
.
7.10.а)![]() при
при![]() ,
,![]() ,
,![]() ;
;
б)![]() ;в)
;в)![]() ;г)
;г)![]() .
.
а)
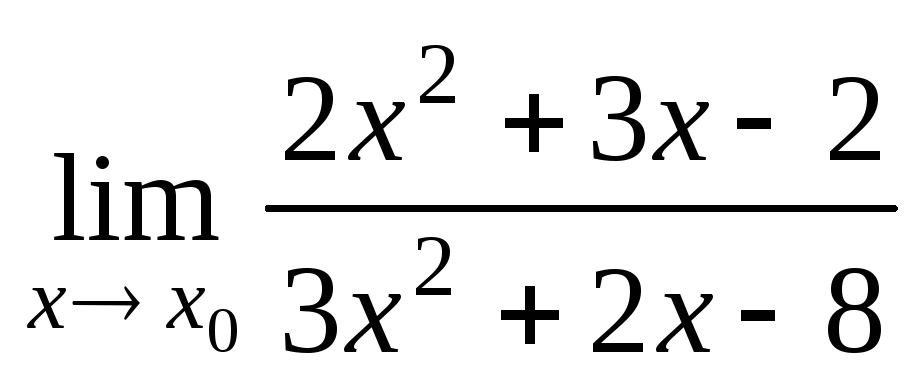 при
при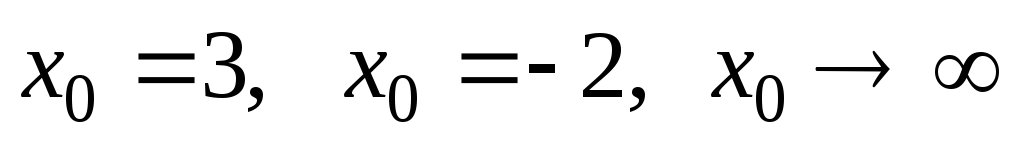 ;
;
б)
![]() ;
в)
;
в) ![]() ;
г)
;
г) ![]() .
.
а)
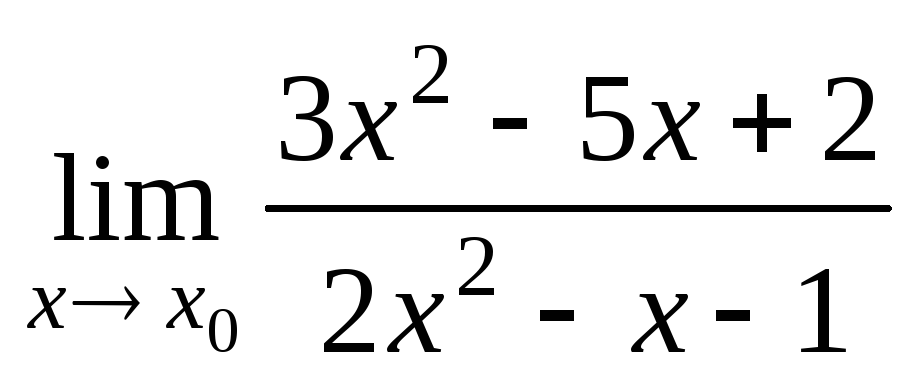 при
при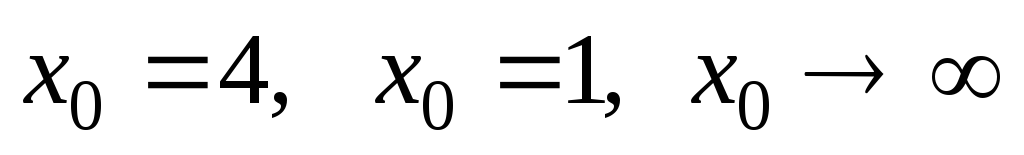 ;
;
б)![]() ;в)
;в)![]() ;г)
;г)![]() .
.
а)
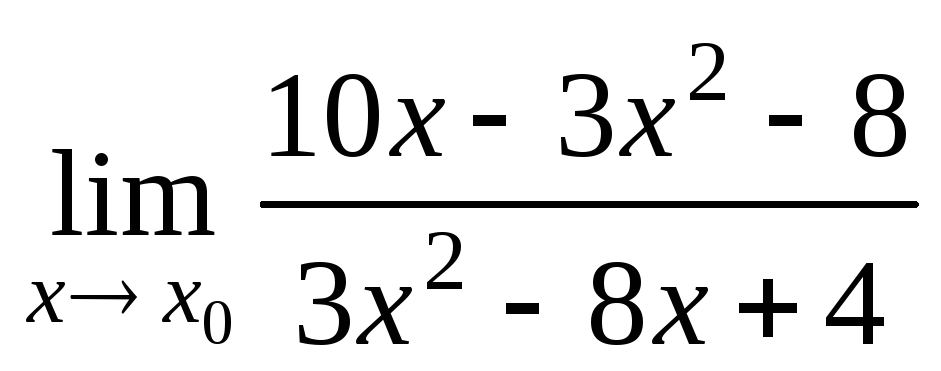 при
при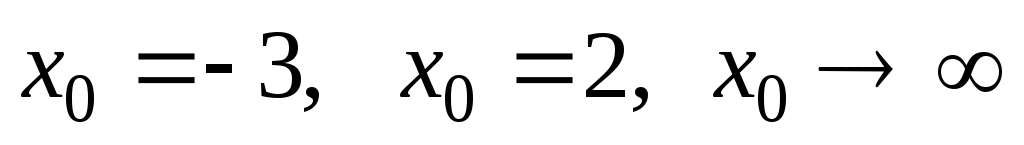 ;
;
б) ![]() ;в)
;в)![]() ;г)
;г)![]() .
.
а)
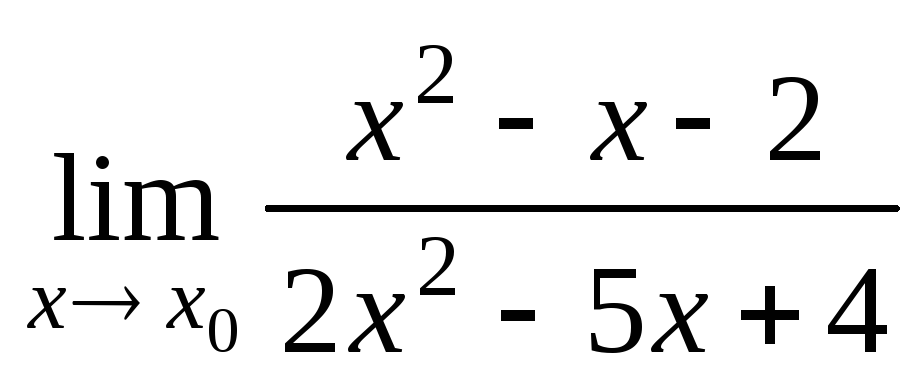 при
при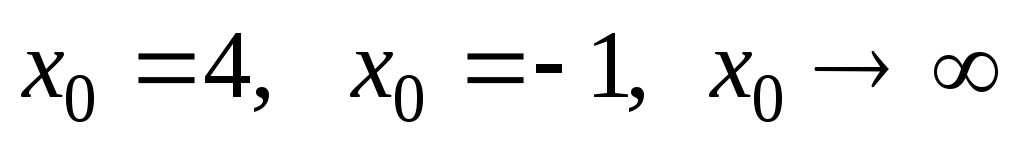 ;
;
б)![]() ;в)
;в)![]() ;г)
;г)![]() .
.
а)
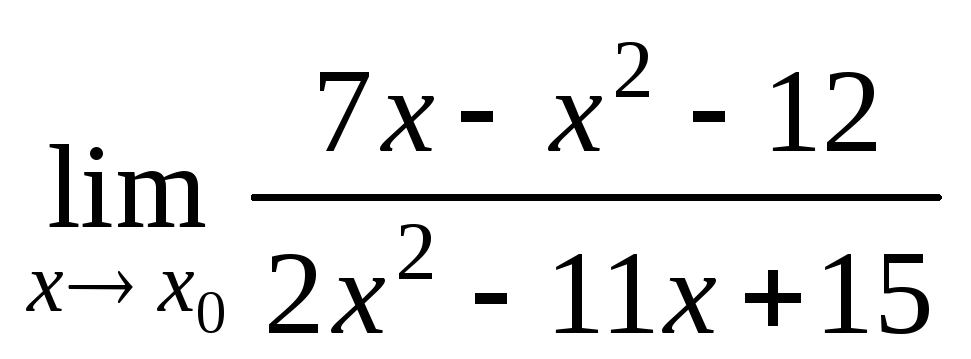 при
при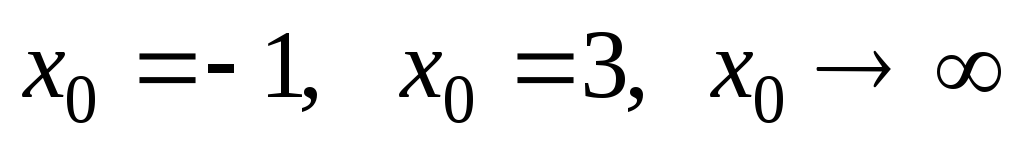 ;
;
б)
![]() ;
в)
;
в) ![]() ;
г)
;
г) ![]() .
.
а)
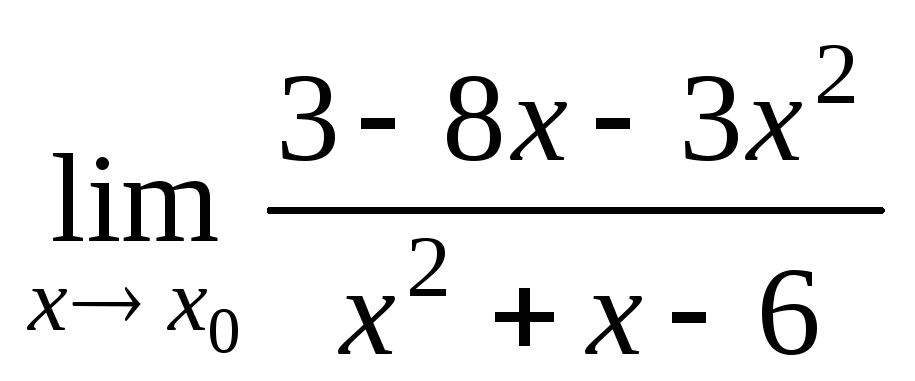 при
при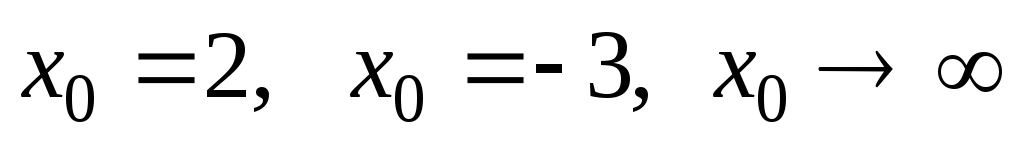 ;
;
б)
![]() ;
в)
;
в) ![]() ;
г)
;
г) ![]() .
.
а)
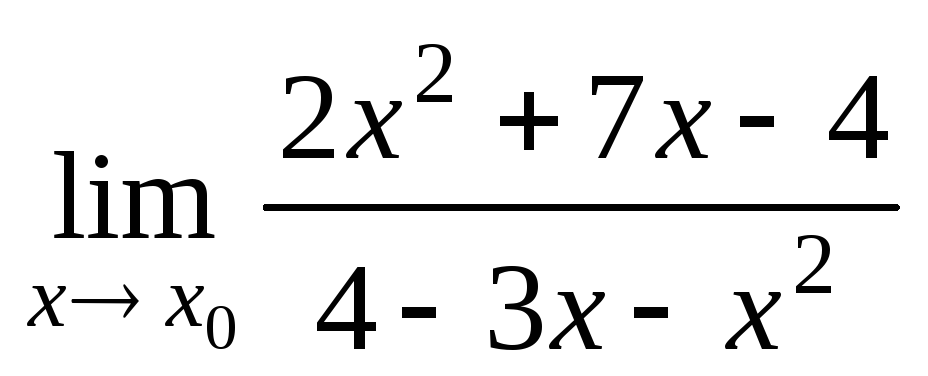 при
при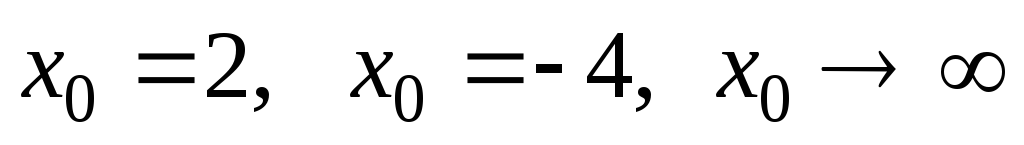 ;
;
б)
![]() ;
в)
;
в) ![]() ;
г)
;
г) ![]() .
.
а)
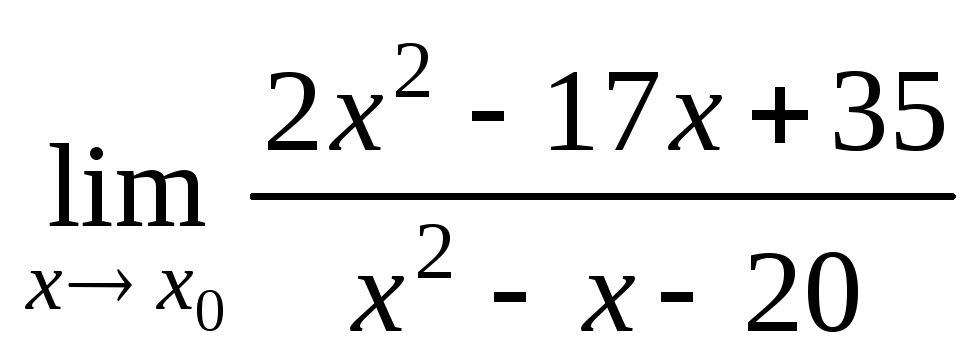 при
при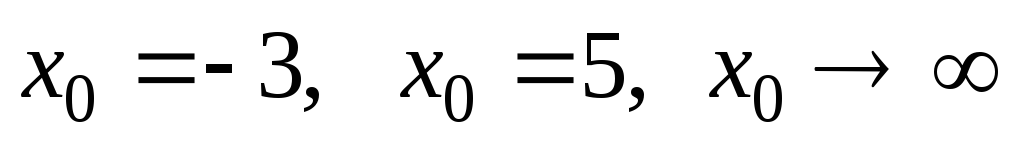 ;
;
б)![]() ;в)
;в)![]() ;г)
;г)![]() .
.
а)
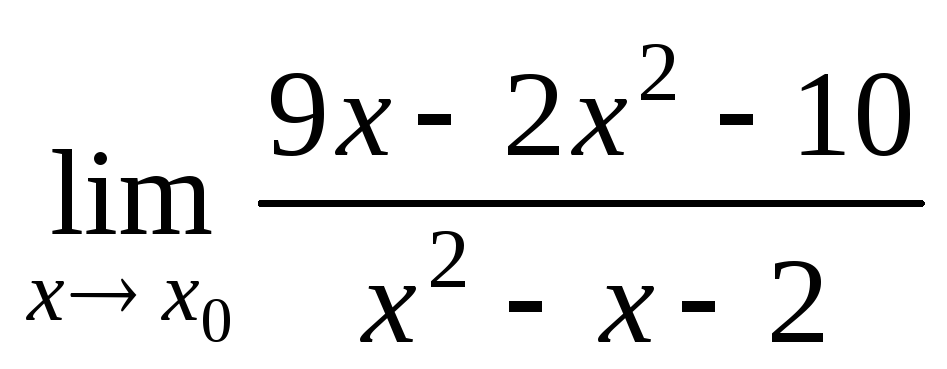 при
при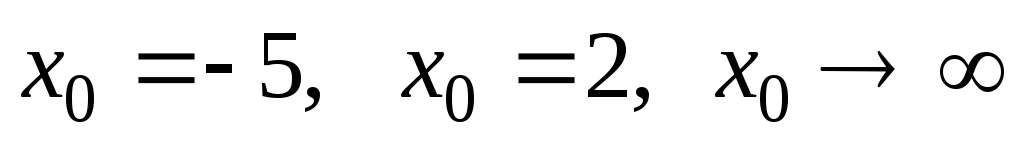 ;
;
б)
![]() ;
в)
;
в) ![]() ;
г)
;
г) ![]() .
.
а)
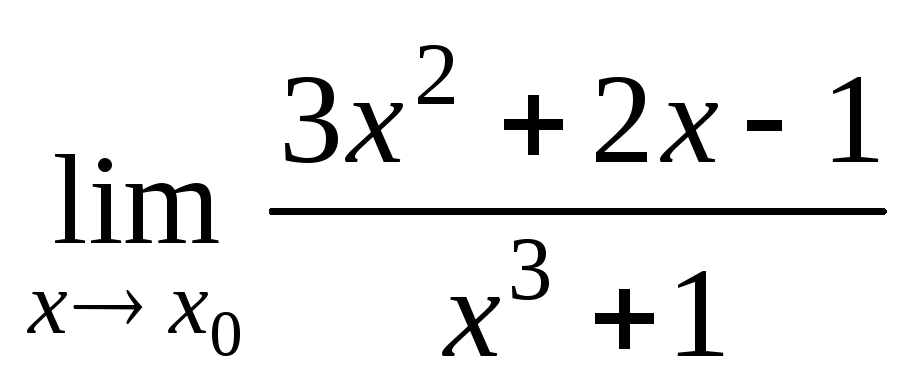 при
при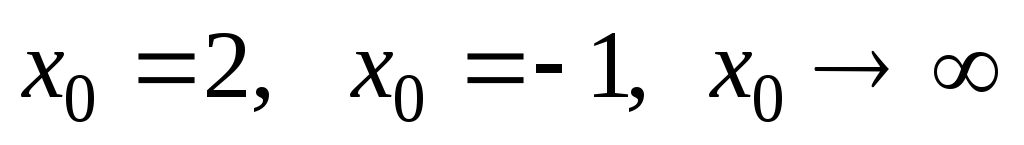 ;
;
б)
![]() ;
в)
;
в) ![]() ;
г)
;
г) ![]() .
.
а)
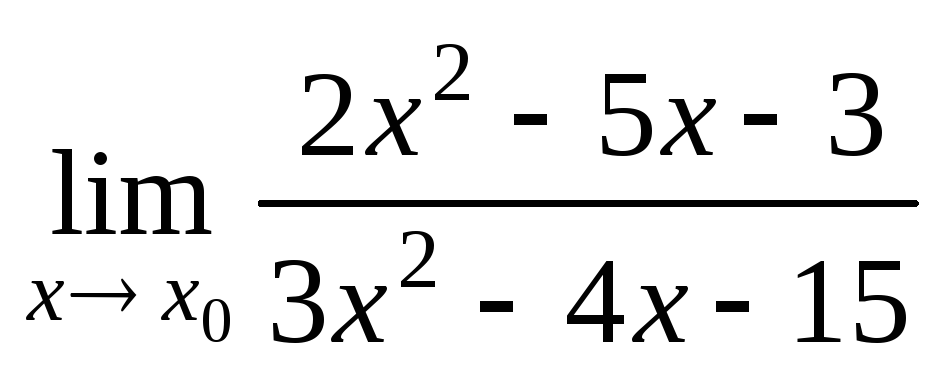 при
при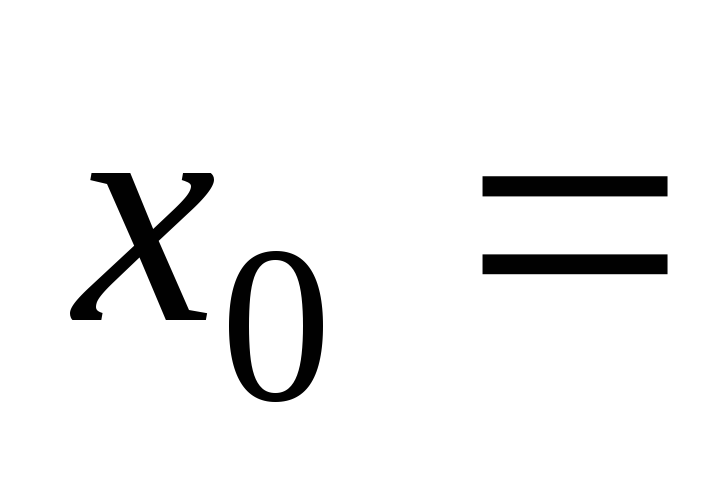 2,
2,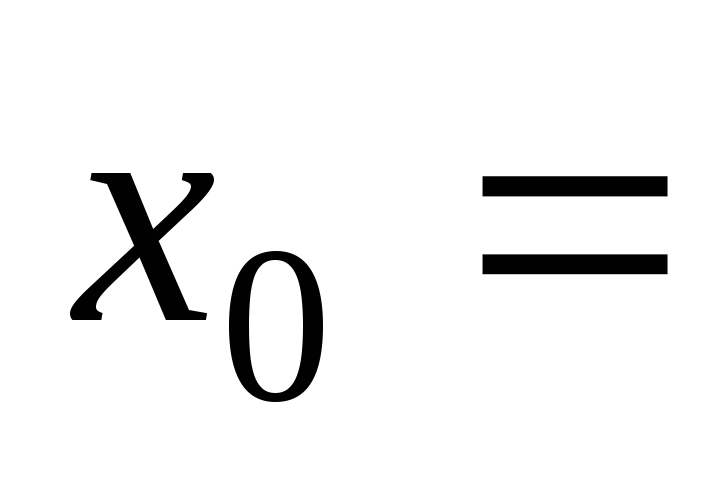 3,
3,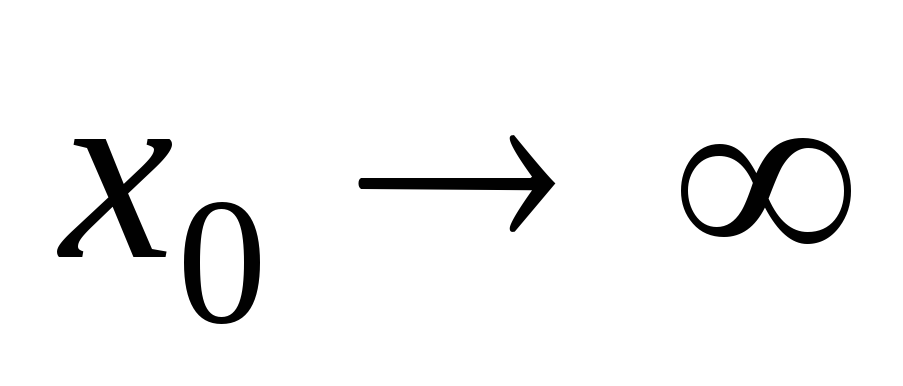 ;
;
б)![]() в)
в)![]()
![]()
а)
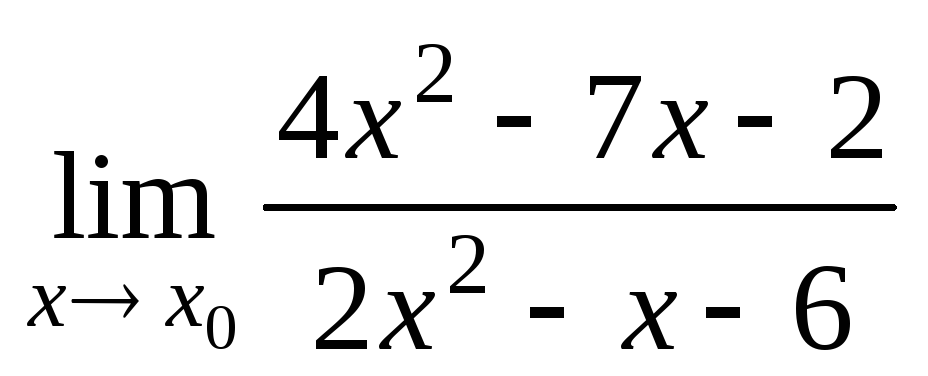 при
при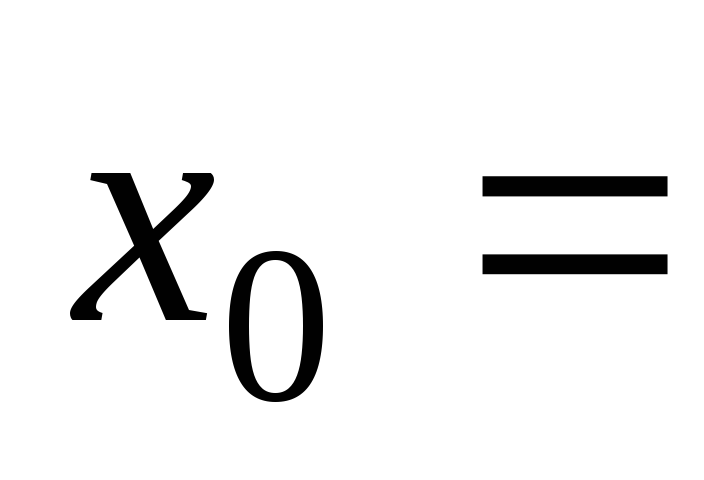 0,
0,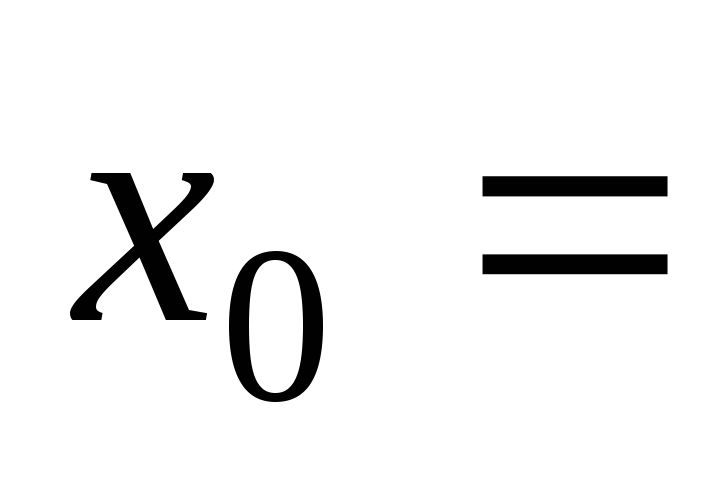 2,
2,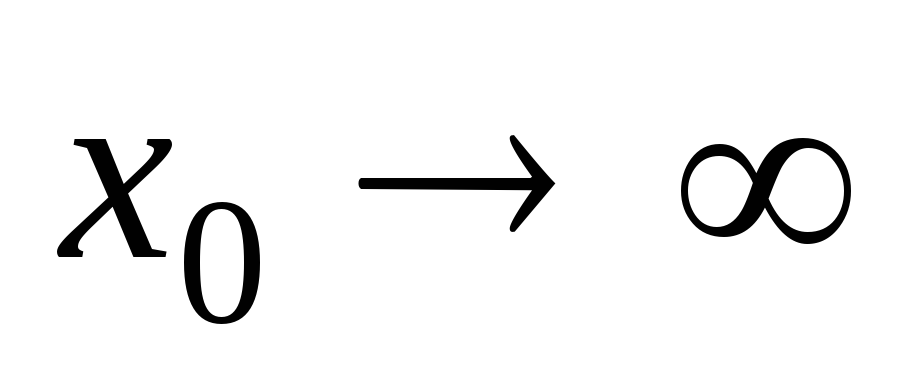 ;
;
б)![]() в)
в)![]()
![]()
а)
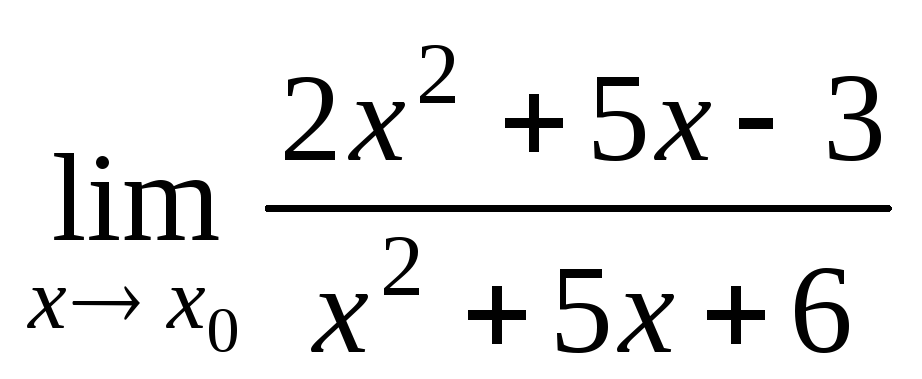 при
при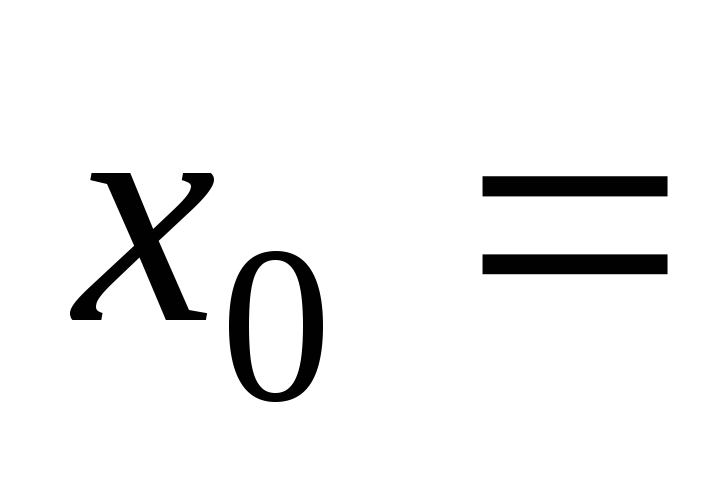 3,
3,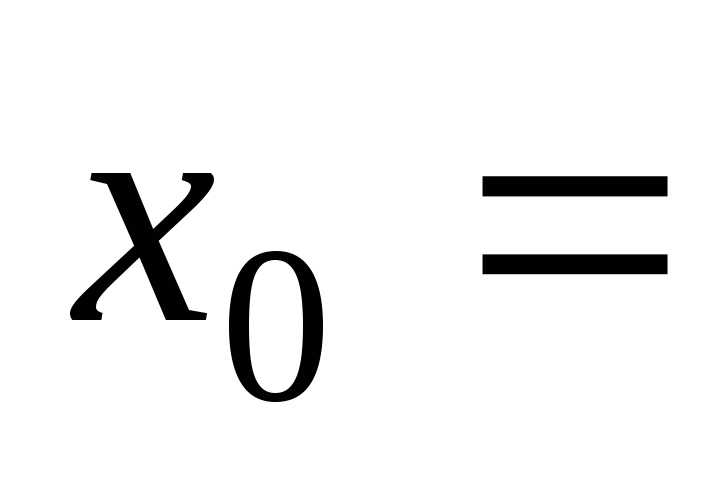 –3,
–3,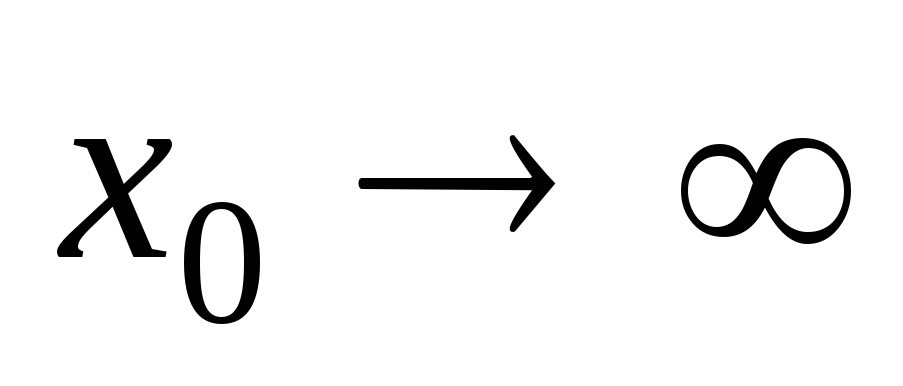 ;
;
б)![]() в)
в)![]()
![]()
а)
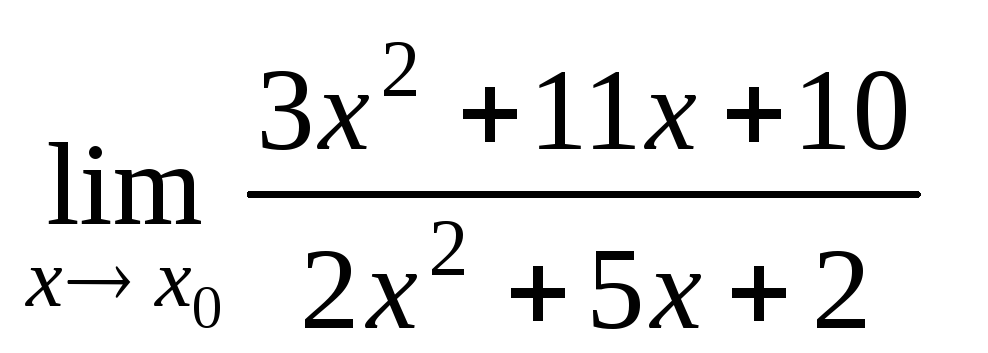 при
при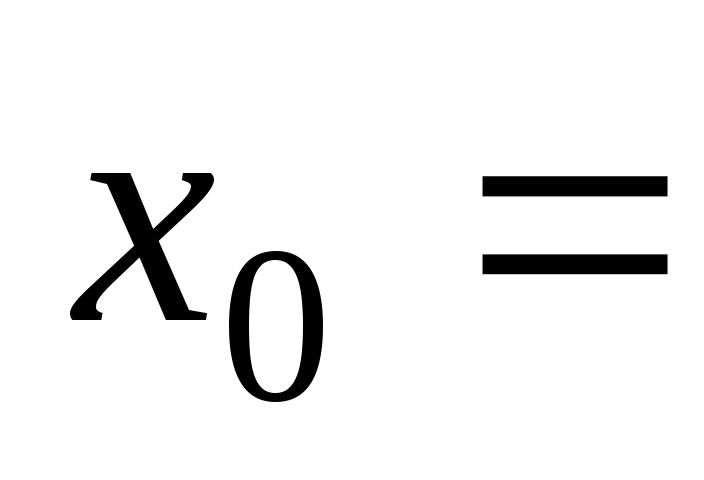 –3,
–3,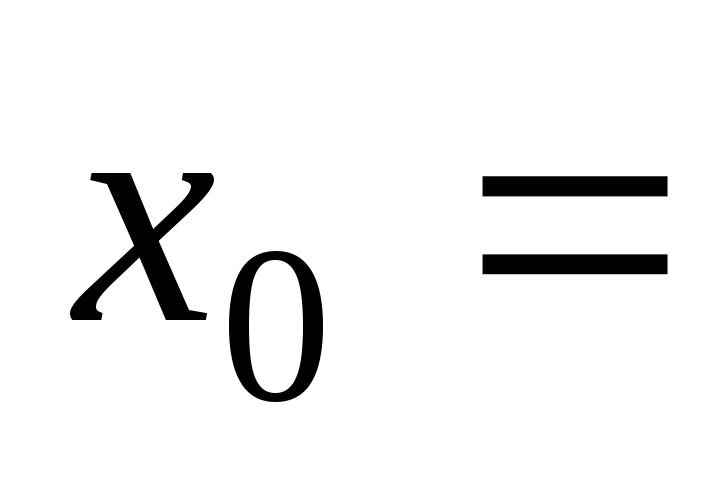 –2,
–2,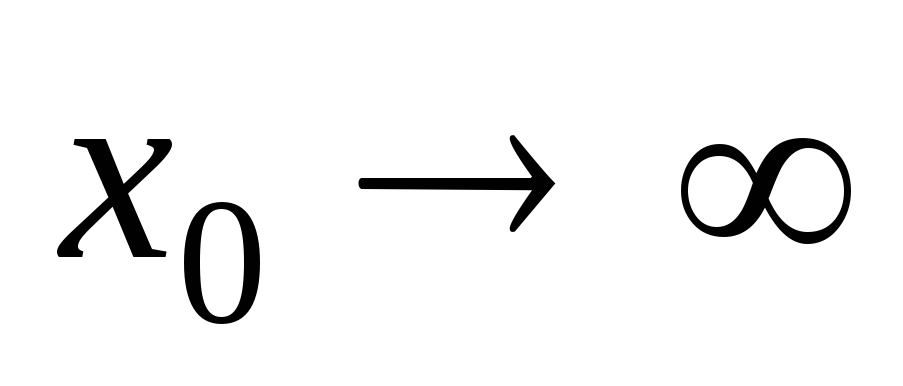 ;
;
б)![]() в)
в)![]()
![]()
а)
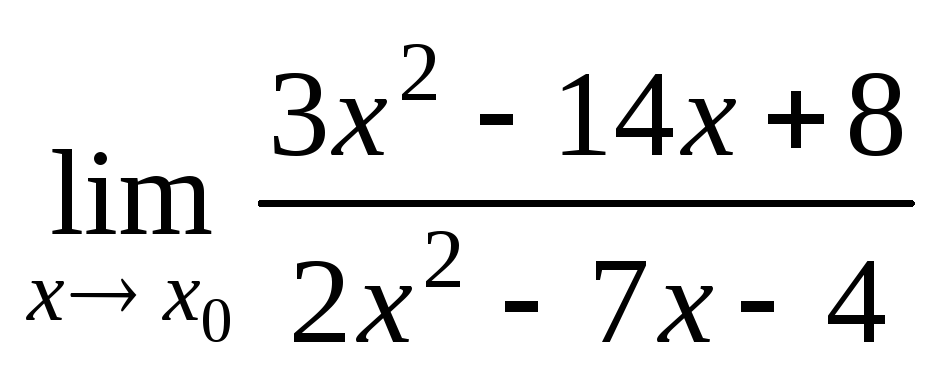 при
при 2,
2,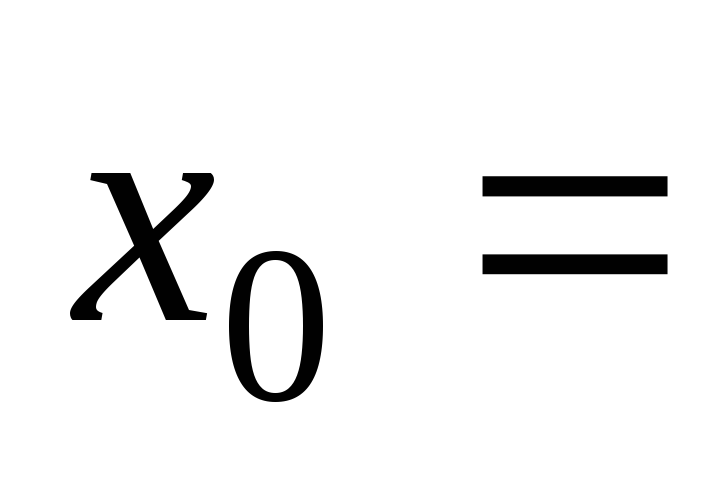 4,
4,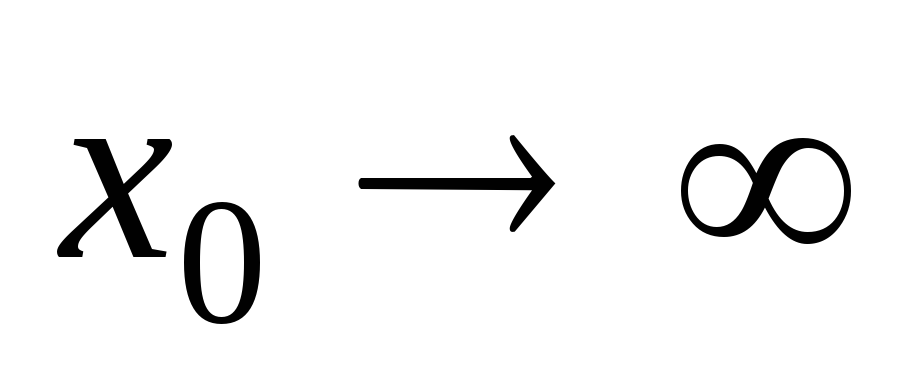 ;
;
б)![]() в)
в)![]()
![]()
а)
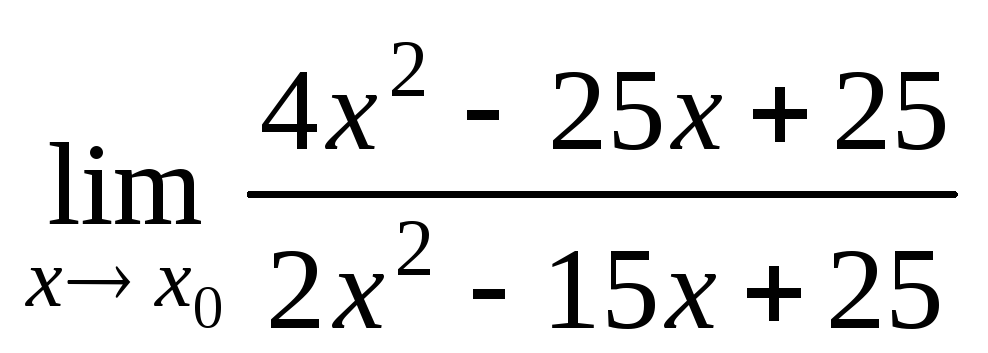 при
при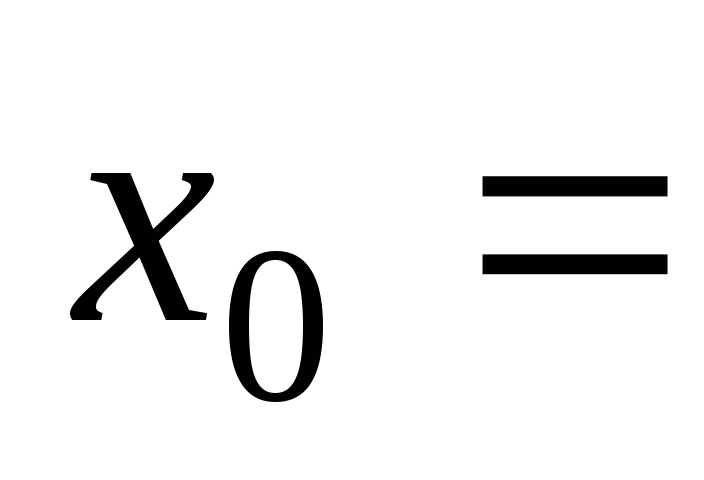 2,
2,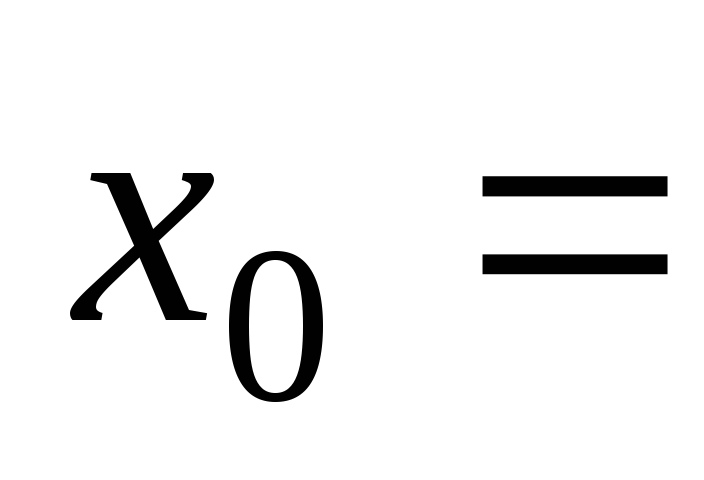 5,
5,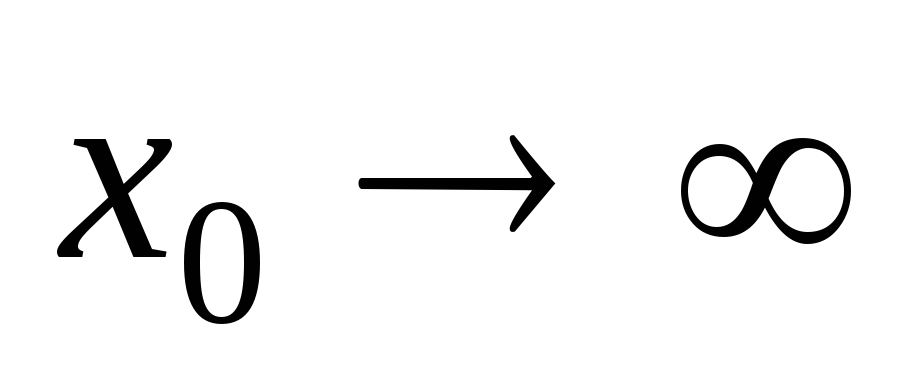 ;
;
б)![]() в)
в)![]()
![]()
а)
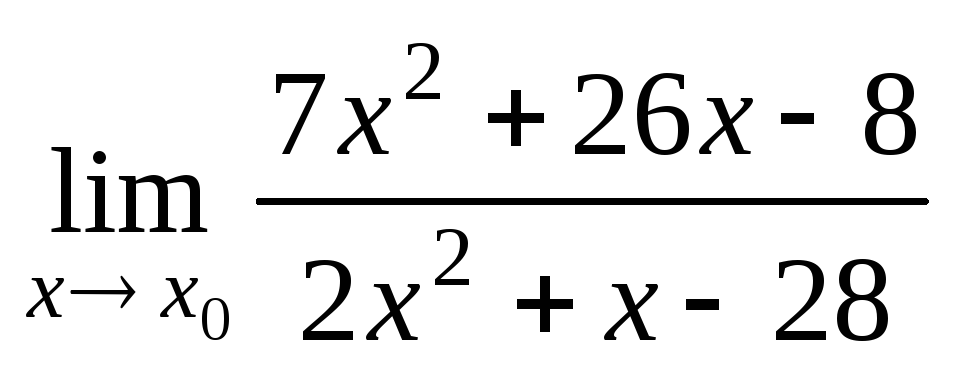 при
при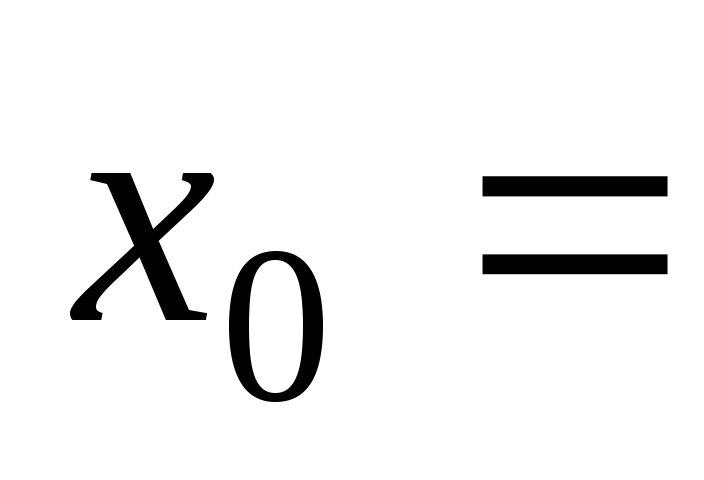 1,
1,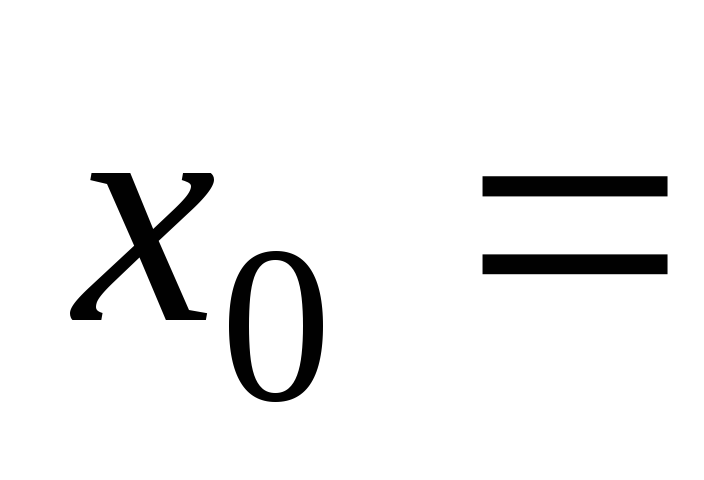 –4,
–4,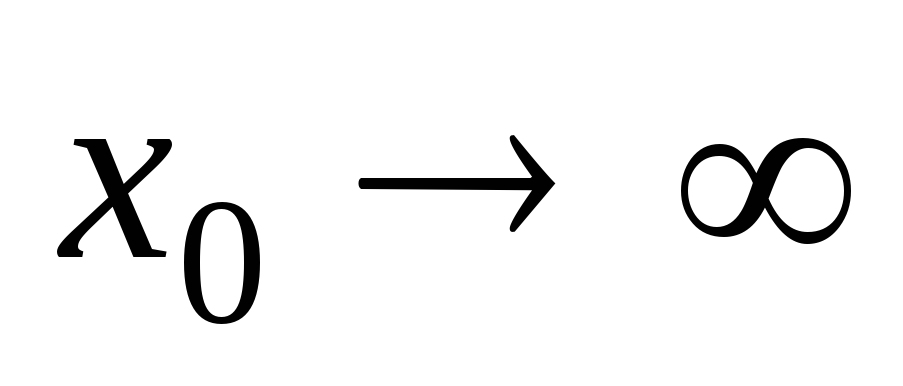 ;
;
б)![]() в)
в)![]()
![]()
а)
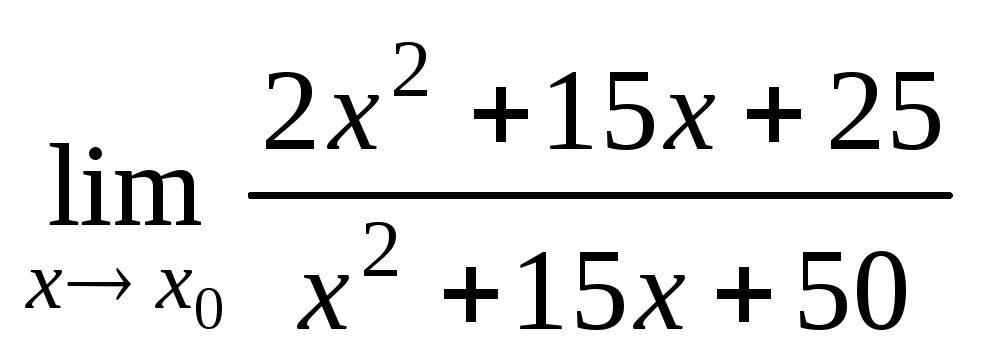 при
при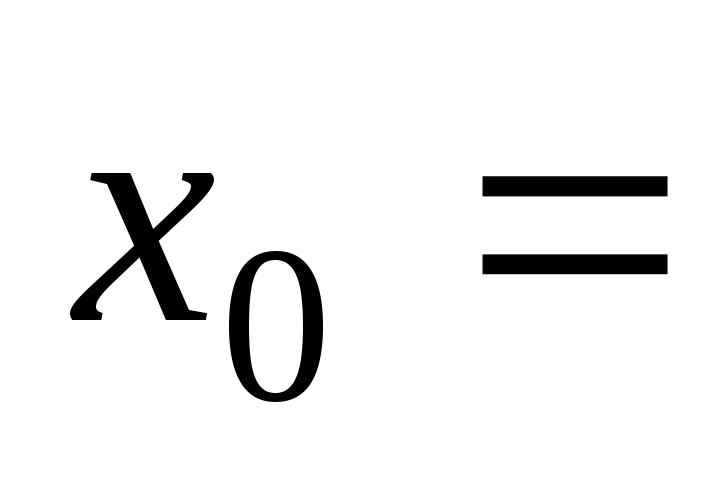 5,
5,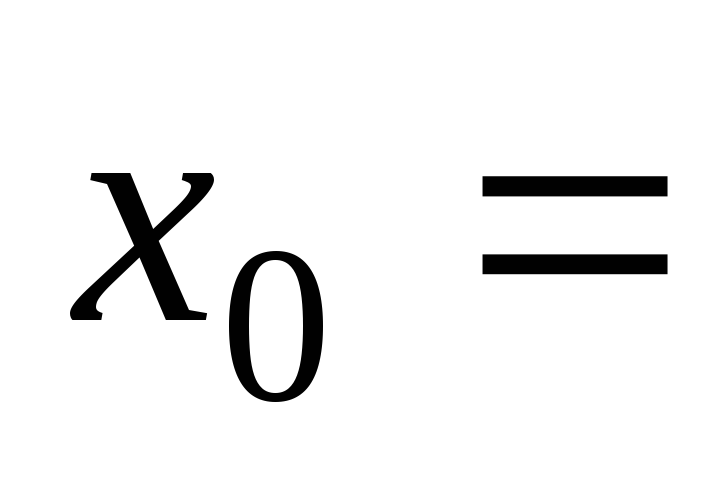 –5,
–5,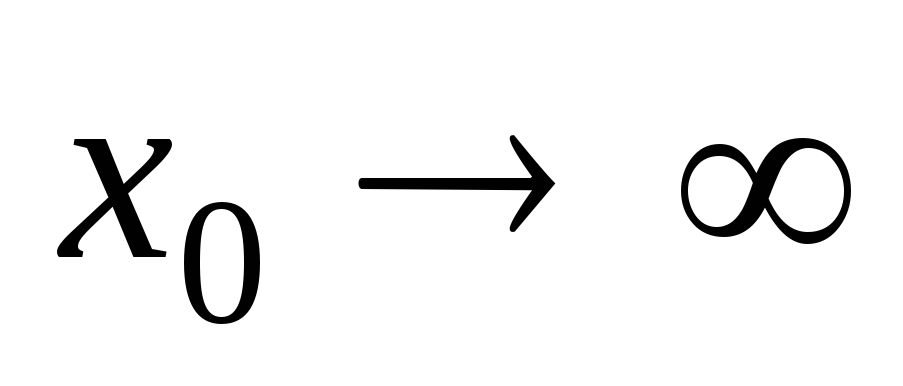 ;
;
б)![]() в)
в)![]()
![]()
а)
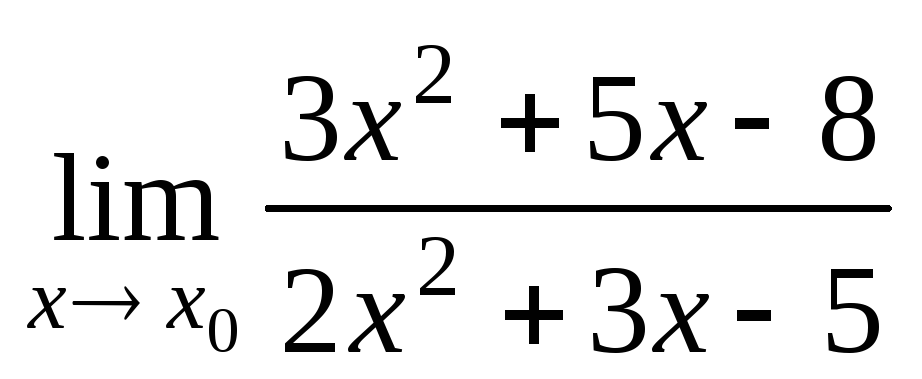 при
при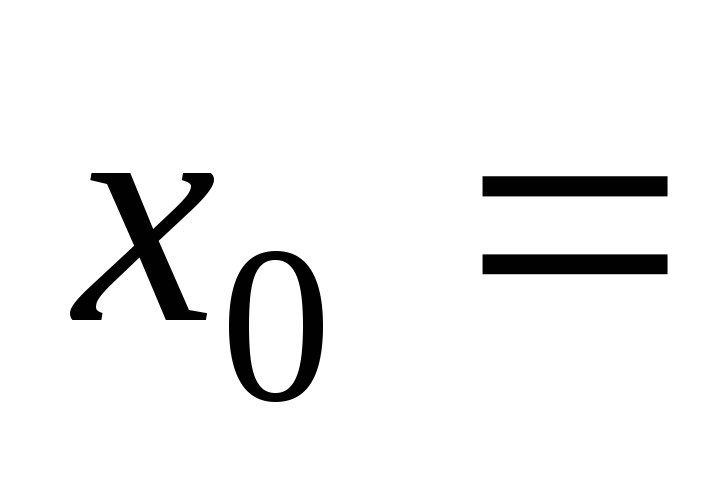 –2,
–2,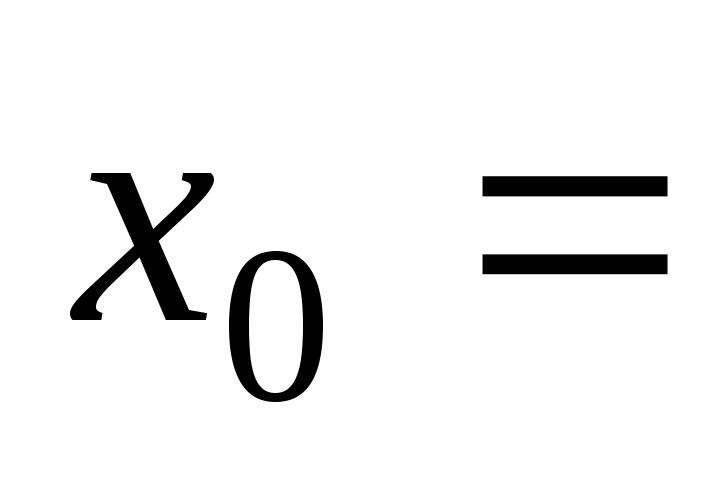 1,
1,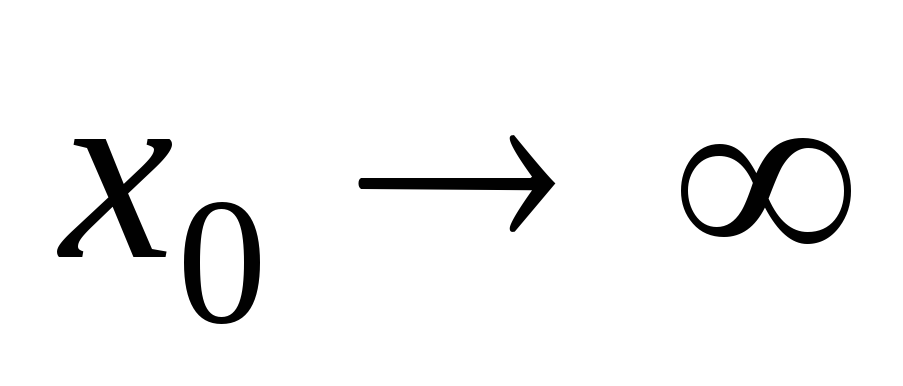 ;
;
б)![]() в)
в)![]()
![]()
а)
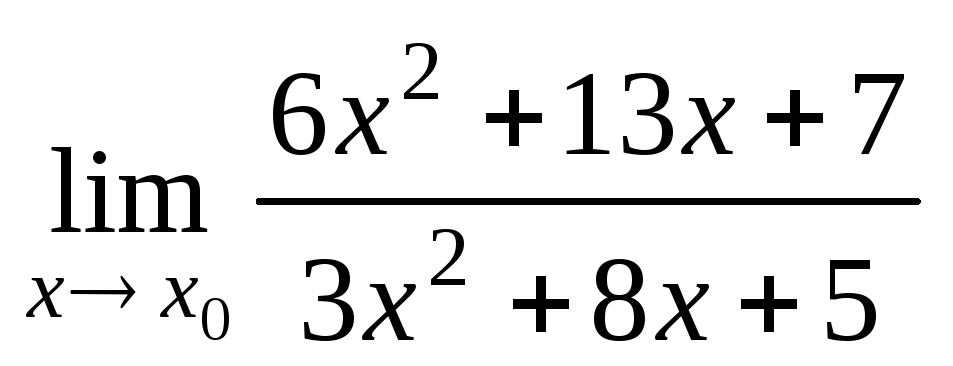 при
при –2,
–2,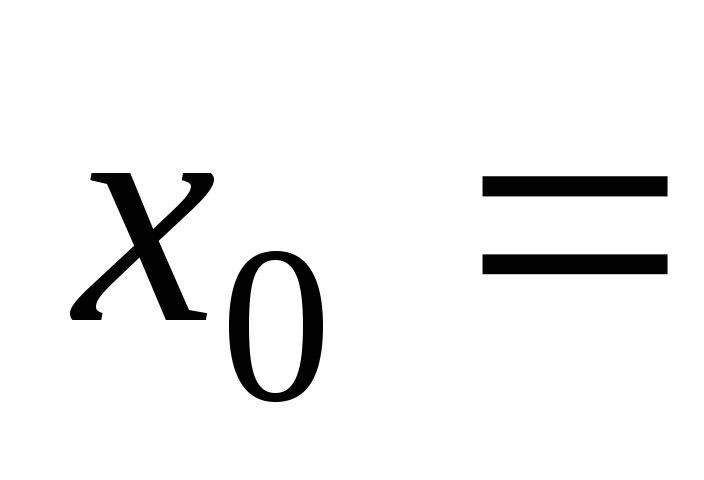 –1,
–1,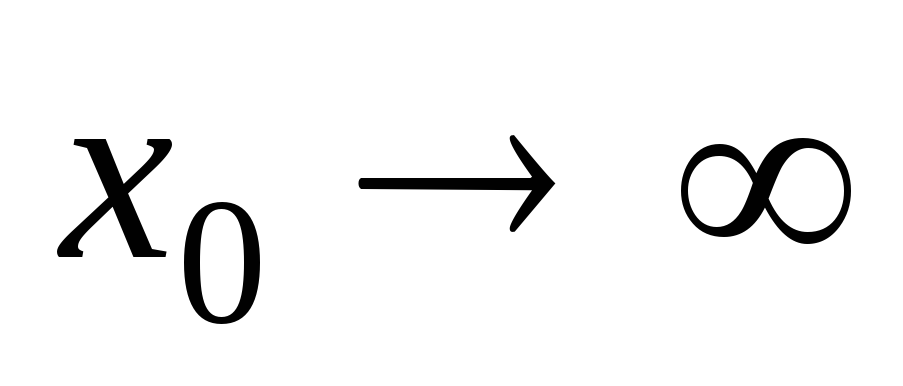 ;
;
б)
![]() в)
в)
![]()
![]()
Задание № 8
Задана функция y = f (x). Установить, является ли данная функция непрерывной. В случае разрыва функции в некоторой точке найти ее пределы слева и справа, классифицировать характер разрыва. Построить схематично график функции.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|