Взаимное пересечение поверхностей

Общим способом построения линий пересечения одной поверхности другой является нахождение точек этой линии при помощи некоторых секущих плоскостей или вспомогательных секущих сфер. Ниже будет показано решение задач на определение линий пересечения поверхностей с помощью вспомогательных секущих плоскостей цилиндрических, конических, сферических поверхностей, а также пример построения линий пересечения с помощью вспомогательных секущих сфер.

Построение линий пересечения поверхности с помощью вспомогательных секущих плоскостей

При построении линии пересечения двух поверхностей вспомогательные секущие поверхности выбирают такими, чтобы они, пересекаясь с данной поверхностью, давали бы простые для построения линии (например, прямые или окружности).

Часто за вспомогательные секущие поверхности принимаются либо плоскости, либо сферы. При решении задач на построение линий пересечения поверхностей вспомогательные секущие плоскости обычно выбирают в виде плоскостей уровня – плоскостей, параллельных плоскостям проекций.

Линии двух поверхностей имеют характерные (опорные, главные) точки, с которых и следует начинать построение линий пересечения. Они позволяют видеть, в каких границах можно изменять положение вспомогательных секущих плоскостей для определения произвольных точек.

Способ определения линии пересечения поверхности с помощью плоскостей, - ось которого – собственная прямая.

Этот способ применяется для построения линий пересечения:

а) двух конических поверхностей;

б) конической и цилиндрической поверхности;

в) конической поверхности с поверхностью пирамиды или призмы;

г) двух цилиндрических поверхностей;

д) цилиндрической поверхности с поверхностью пирамиды или призмы.

Рассмотрим несколько следующих задач.

1. Построить линии пересечения цилиндра и конуса, оси которых не пересекаются (рис.7).

Обе данные поверхности рассечены вспомогательными плоскостями I₂, II₂, III₂ и прочими, параллельными плоскости П₁.

Тогда на горизонтальной проекции конуса получится ряд концентрических окружностей, обозначенных теми же номерами, а на проекции цилиндра – ряд образующих.

В пересечении образующих с соответствующими окружностями определяются горизонтальные проекции точек искомого сечения а, в, с и прочие, по которым затем находят их фронтальные проекции.

Найденные проекции точек соединяют плавными кривыми. Невидимые части линии пересечения проведены штрихами на обеих проекциях.

Границей между видимой и невидимой частями линий пересечения являются крайние образующие цилиндра.

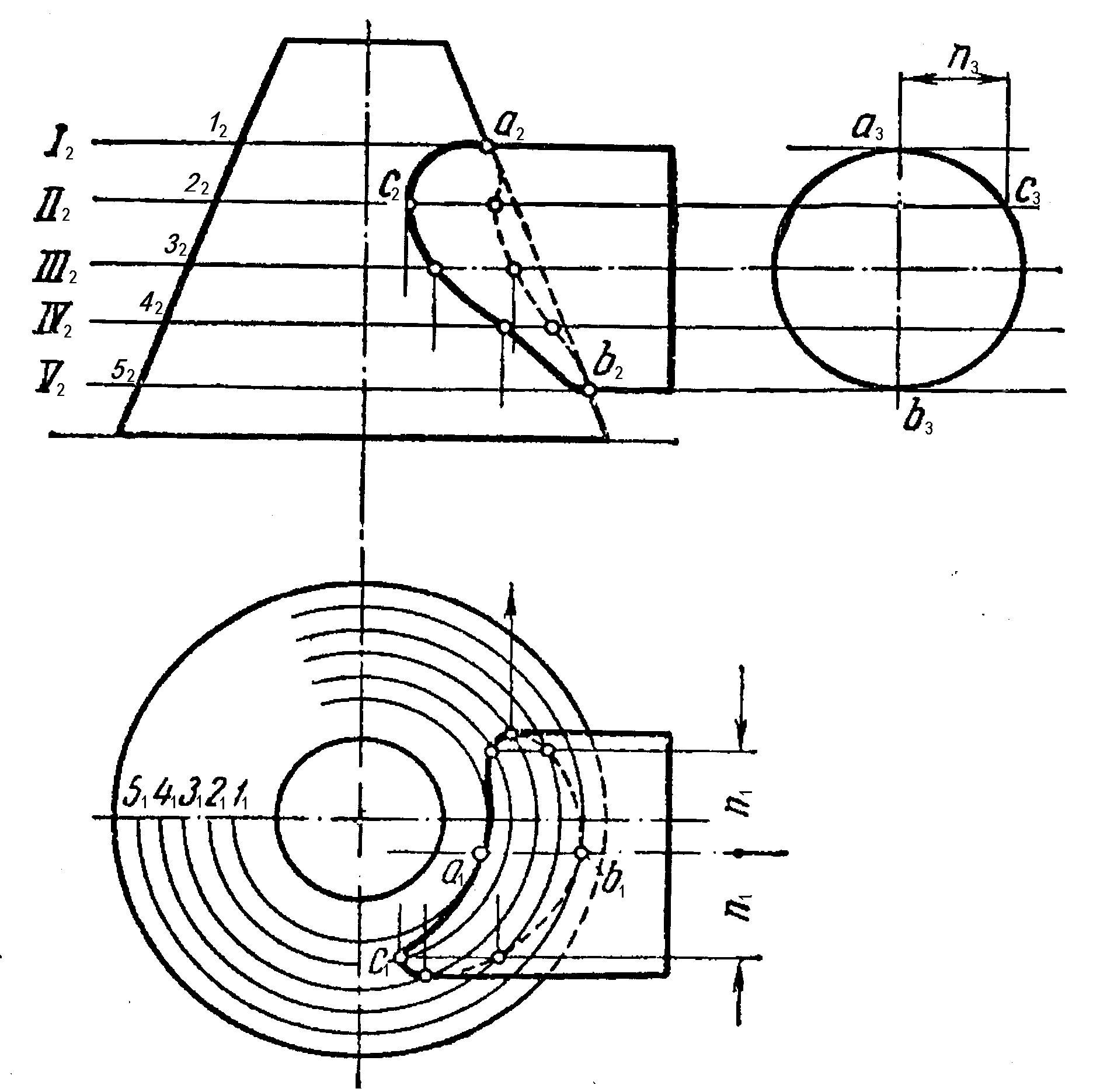
Pис. 7

Такие наиболее характерные точки линий пересечения кривых поверхностей следует строить в первую очередь, т.е. начинать работу с определения точек, в которых крайние (очерковые) образующие каждой поверхности, ограничивающие ее контур видимости на П₁, П_2, пересекают другую поверхность. После этого находят проекции нескольких промежуточных точек.

Если кривая поверхность пересекается с многогранником, то контур линии пересечения состоит из нескольких кривых частей, пересекающихся между собой на ребрах многогранника, следовательно, в этих точках криволинейный контур имеет резкие изломы. Эти характерные точки следует определять в первую очередь.

На рис. 8 таковыми являются точки (1₁, 1₂), (2₁, 2₂), (3₁, 3₂), (4₁, 4₂), в которых ребра призмы пронизывают поверхность конуса.

В обоих рассмотренных примерах легко выбрать вспомогательные секущие плоскости так, чтобы в пересечении их с каждой из данных поверхностей получились простые линии – окружности или прямые. Особенность этих примеров состояла в том, что одна из данных поверхностей была проецирующей (т.е. ее образующие или ребра были перпендикулярны к одной из плоскостей проекций).

Рис.8

В таких случаях одна из проекций искомой линии уже имеется на эпюре: она совпадает с соответствующей проекцией той из данных поверхностей, которая является проецирующей (например, с профильной цилиндра на рис.7 или с фронтальной рис.8).

Вся задача сводится в сущности к нахождению по одной известной заранее проекции линии пересечения других ее проекций.

Затем найдены еще две характерные точки (5₁, 5₂) и (6₁, 6₂), в которых крайняя образующая конуса пересекает грани призмы. После этого можно найти проекции нескольких промежуточных точек, в которых другие образующие конуса пересекают грани призмы (7₁, 7₂; 8₁, 8₂; 9₁, 9₂; 10₁, 10₂).

Рассмотрим еще один пример построения линии пересечения двух поверхностей полусферы и цилиндра (рис.9).

Рис.9

Рисунок 9 иллюстрирует решение задачи по определению линии L=α∩β, при этом β перпендикулярен П₁. Вводя вспомогательные секущие плоскости f₁, f₁¹, f₁¹¹ и т.д. строим фронтальную проекцию L₂ – линии пересечения сферической поверхности α с поверхностью горизонтально-проецирующего прямого кругового цилиндра β.

Точка А₁, принадлежащая линии пересечения поверхностей, и является ближайшей к вертикальной оси ι поверхности сферы, одновременно будет высшей точкой А₂ на фронтальной проекции кривой L₂. Точка В₂ – крайняя правая на линии пересечения является также границей видимой кривой L₂.

Пример: Найти линию пересечения двух цилиндров (рис.10)

Вводим вспомогательные плоскости R₁ R₁¹ параллельно плоскости П₂ и пересекаем поверхности цилиндров по образующим. На их пересечении получаем точки (1₁, 1₂) и (2₁, 2₂). Аналогично находим еще ряд произвольных точек. Затем находим характерные точки а, b, c, d, e, f при помощи вспомогательных плоскостей S₁, S₁¹, S₁¹¹, S₁¹¹¹. Соединив все найденные точки кривой линией, получаем искомую линию пересечения.

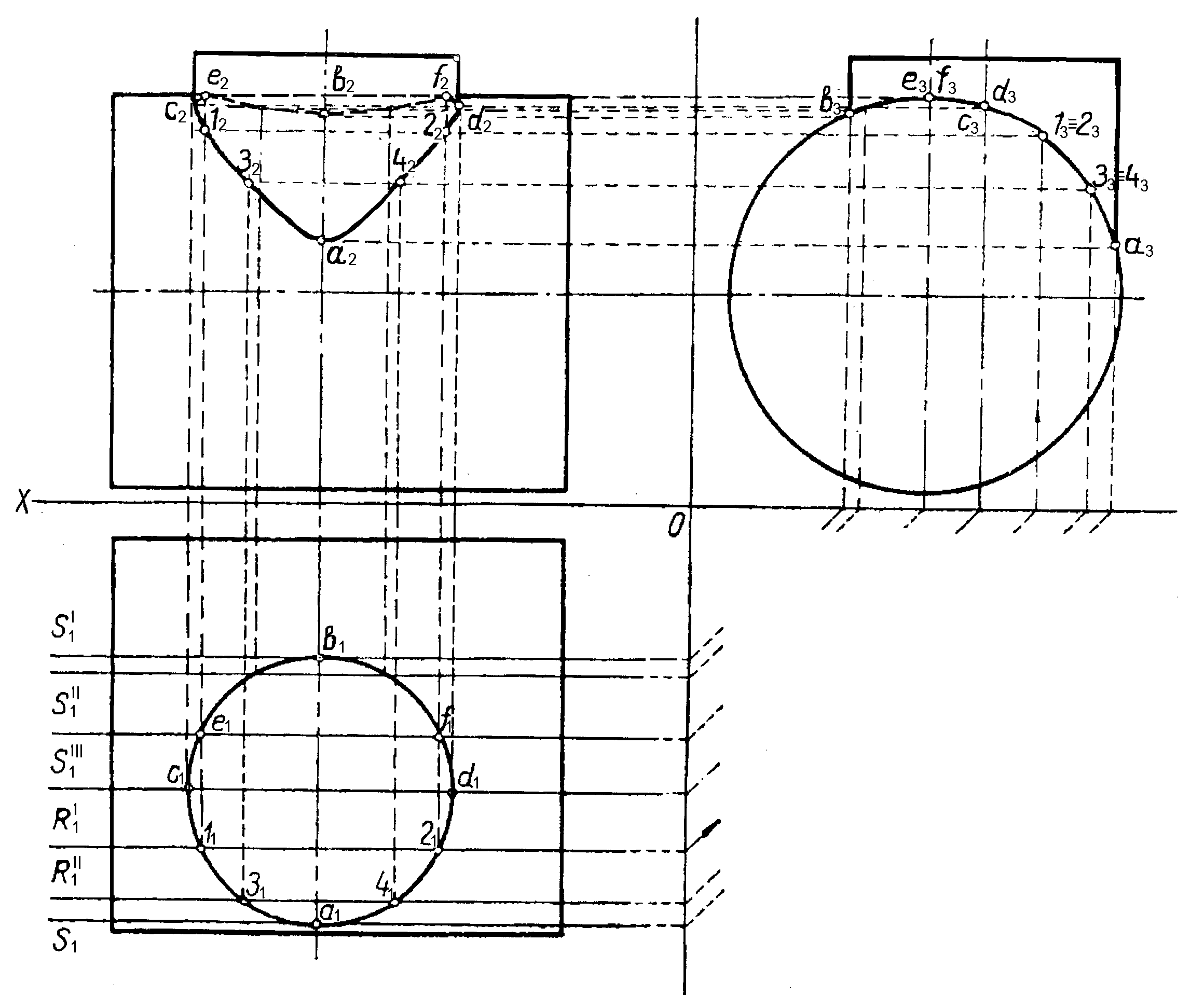
Рис.10

Для построения точек линии, получающейся на одной поверхности при пересечении ее другой поверхностью, пользуются вспомогательными секущими плоскостями частного и общего положения, кривыми поверхностями, прямолинейными образующими кривых линейчатых поверхностей и ребрами гранных поверхностей. При этом прибегают к способам преобразования чертежа, если это упрощает и уточняет построение.