
- •Практикум
- •По курсу
- •«Экономико-математические
- •Методы и модели»
- •Содержание
- •Предисловие
- •1 Модель общей задачи линейного программирования
- •2 Транспортные задачи в моделировании
- •3 Экономико-статистическое моделирование и прогнозирование средствами ms Excel
- •4 Модели управления товарными запасами
- •1 Модели управления однономенклатурными запасами
- •1.1 Простейшая модель оптимального размера партии поставки
- •1.2 Модель с конечной интенсивностью поступления заказа
- •1.3 Модель с учетом неудовлетворенных требований
- •1.4 Модель с потерей неудовлетворенных требований.
- •1.5 Модель с определением точки заказа
- •2 Модели управления многономенклатурными запасами
- •5 Системы массового обслуживания
- •1 Одноканальная смо с ожиданием и ограничением на длину очереди
- •2 Одноканальная смо с ожиданием
- •3 Многоканальная смо с отказами
- •4 Многоканальная смо с ожиданием и ограничением на длину очереди
- •5 Многоканальная смо с неограниченной длиной очереди
- •6 Модели сетевого планирования и управления
- •1 Построение сетевого графика и расчет основных параметров сетевой модели
- •5) Определить, на сколько дней можно отложить выполнение работы a6 без отсрочки завершения проекта в целом?
- •2 Оптимизация сетевого графика по времени
- •7 Применение элементов теории игр при принятии управленческих решений
- •1 Решение матричной игры в чистых и смешанных стратегиях
- •2 Решение статистических игр по различным критериям
- •8 Балансовые модели в экономике
- •Литература
- •Приложение а Критические значения f-критерия (распределение Фишера)
- •Приложение б Распределение Стьюдента (t-распределение)
4 Модели управления товарными запасами
-
Формируемые навыки и умения:
- освоение методики решения моделей управления однономенклатурными запасами;
- освоение методики решения моделей многономенклатурными запасами.
Теоретическая поддержка
Одним из важнейших этапов планирования работы любой производственной или торговой единицы является определение оптимального уровня запасов сырья, полуфабрикатов, товаров или продукции.
Под запасом понимается годный к употреблению, но не используемый в настоящее время ресурс. Создание и хранение запасов обуславливает наличие различного рода издержек, таких как: издержки, связанные с приобретением партии, затраты на оформление заказа, издержки хранения запаса, издержки, связанные с отсутствием запасов, и т. д.
В целом управление запасами включает задачи анализа, прогноза, планирования и нормирования. Перечисленные задачи можно решать с помощью методов и моделей теории управления запасами. Целью теории является разработка методов и моделей выбора таких параметров управления, при которых достигается оптимум (минимум или максимум) какого-либо критерия оптимальности, например минимум затрат, максимум прибыли, минимум времени и др.
Одним из важнейших направлений управления запасами является их оптимизация. Под оптимальным запасом следует понимать минимально необходимый размер товарного запаса, обеспечивающий бесперебойное обеспечение товарами в соответствии со спросом при минимальном уровне затрат на приобретение и хранение, а также минимальными потерями от дефицита.
Решение задач определения оптимальных параметров управления запасами зависит от:
- характера спроса на товарную продукцию (детерминированный или вероятностный);
- времени пополнения запаса (мгновенное или равномерное);
- числа видов продукции (однономенклатурные и многономенклатурные модели).
Многономенклатурные модели могут иметь такие ограничения, как дефицит складских площадей, габаритов упаковки и т.п. В этих случаях в параметры моделей, в частности в размеры оптимальных партий, необходимо внести определённые поправки.
1 Модели управления однономенклатурными запасами
1.1 Простейшая модель оптимального размера партии поставки
Эта модель позволяет определить такой размер заказываемой партии, который минимизирует расходы на организацию заказа и содержание его на складе. Экономичная партия поставки вычисляется при следующих допущениях. Уровень запасов снижается равномерно с интенсивностью v (спрос). В момент, когда все запасы исчерпаны, подается заказ на поставку новой партии размером q ед. Заказ выполняется мгновенно, то есть время доставки заказа пренебрежимо мало и уровень запасов восстанавливается до максимального значения, равного q. Накладные расходы, связанные с размещением заказа и поставкой партии, не зависят от объема партии и равны постоянной величине К. Издержки содержания единицы товара на складе в единицу времени равны s. Срыв поставок недопустим. Пусть I(t) – уровень запасов в зависимости от времени; τ — интервал времени между поставками. Процесс изменения уровня запасов I показан на рисунке 4.1.
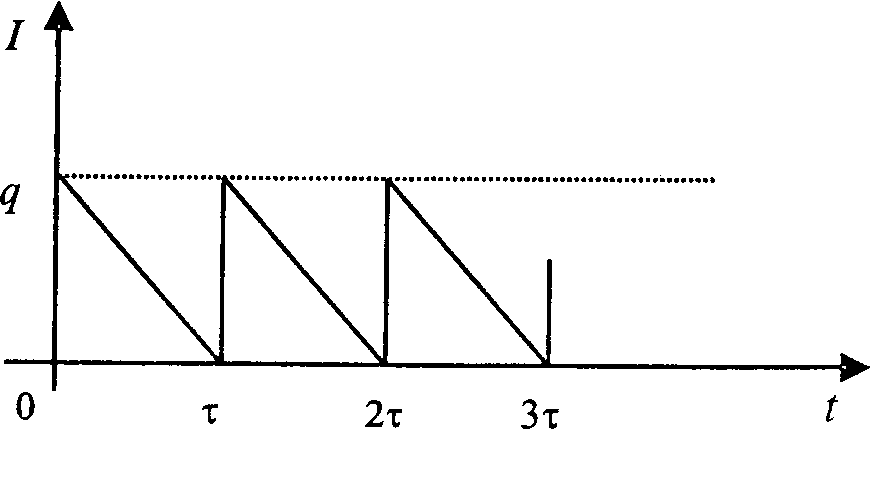
Рисунок 4.1 - Простейшая модель оптимального размера партии поставки
Таблица 4.1 – Показатели модели и формулы для их расчета
|
№ |
Показатели модели |
Формулы для расчета показателей модели |
|
1 |
Интервал времени между поставками |
|
|
2 |
Общие затраты в единицу времени |
|
|
3 |
Общие затраты, связанные с хранением и заказом товара |
|
|
4 |
Оптимальный размер партии заказа (формула Уилсона) |
|
|
5 |
Оптимальный интервал между поставками |
|
|
6 |
Оптимальный средний уровень текущего запаса |
|
|
7 |
Потребление за плановый период |
Q = vТ |
|
8 |
Оптимальное число поставок |
|
|
9 |
Суммарные затраты по формированию поставок и содержанию запасов в единицу времени |
|
Пример решения задачи
Постановка задачи. На склад доставляются бакалейные товары партиями по 1500 т. В сутки со склада потребители забирают 50 т товара. Накладные расходы по доставке партии бакалейных товаров равны 2 млн. ден. ед. Издержки хранения 1 т товара в течение суток равны 100 ден. ед.
Требуется определить:
1) длительность цикла, среднесуточные накладные расходы и среднесуточные издержки хранения;
2) эти же величины для размеров партии в 500 т и в 3000 т;
3) оптимальный размер заказываемой партии и расчетные характеристики работы склада в оптимальном режиме.
Решение задачи
Параметры работы склада:
ν = 50 т/сут.; К = 2 млн. ден. ед.; s = 100 ден. ед./тсут.; q = 1500 т.
1)
Длительность цикла:
![]()
Среднесуточные
накладные расходы:
![]()
Среднесуточные издержки хранения:
![]()
2) Аналогичные расчеты проведем для q1 = 500 т и для q2 = 3000 т.
3) Найдем оптимальный размер заказываемой партии по формуле Уилсона из 4-й строки таблицы 4.1:
![]()
- оптимальный средний уровень запаса по формуле (6-я строка таблицы 4.1):
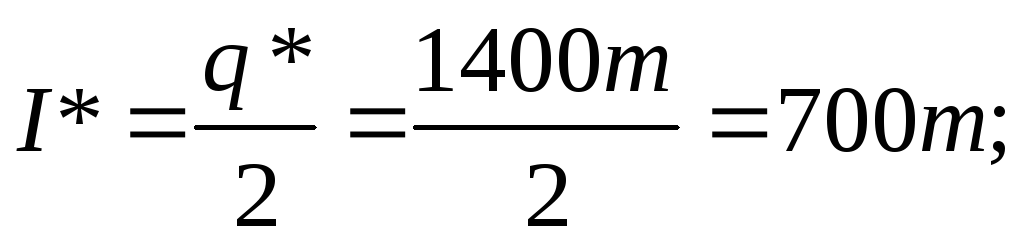
- оптимальную периодичность пополнения запасов по формуле (5-я строка таблицы 4.1):

- оптимальные средние издержки хранения запасов в единицу времени по формуле из 9-й строки таблицы 4.1:
![]()



