20 Лекция №19.Гамильтоновы и эйлеровы графы

Продолжительность:2 часа (90 мин.)

20.1 Ключевые вопросы

20 Лекция №19. гамильтоновы и эйлеровы графы 1

20.1 Ключевые вопросы 1

20.2 Текст лекции 1

20.2.1 Обходы графа 1

20.2.2 Степени вершин 1

20.2.3 гамильтоновы и эйлеровы графы 4

20.2.4 Вопросы для контроля к п. 20.2.1…20.2.3 5

20.2.5 Эйлеровы графы 5

1. Алгоритм построения эйлерова цикла 6

2. Алгоритм построения эйлеровой цепи 6

3. Модифицированный алгоритм построения эйлерова цикла 6

4. Покрытие графа непересекающимися по ребрам цепями 7

20.2.6 вопросы для контроля к п. 20.2.5 9

20.2 Текст лекции

20.2.1 Обходы графа

Обходы графа совершаются с целью поиска вершины или ребра (дуги), обладающей тем или иным признаком. По организации обхода вершин (ребер) различают

• поиск в ширину,

• поиск в глубину.

Для пояснения различий этих поисков по исходному графу построим дерево рис. 20.1 с корнем в вершине – начале обхода (это этаж 1), от этой вершины проводим ребра, инцидентные ей, получаем этаж 2. Затем аналогично строим следующий этаж и т.д.

Рисунок 20.1

Обход в ширину идет просмотром вершин этажа и далее по этажам. Это обслуживание очереди.

Обход в глубину – идем по ветви до конца, если нужная вершина не найдена, то возвращаемся до первого разветвления и далее по новой веточке вниз – обслуживание стека.

20.2.2 Степени вершин

В псевдографе число ребер и дуг (петли либо не учитывают, либо учитывают как два ребра или дуги), инцидентных некоторой вершине х_i, называют степенью вершины (обозначениеdegx_i).

Например, у графа показанного на рис. 20.2

степень вершины: x₁: 6

(ребра е₁,е₂,е₅,е₇,е₈, дугае₃);

степень вершины x₂: 5

(ребра е₁,е₂, дугие₃,e₄,e₆);

степень вершины x₃: 2

(ребро e₅, дуга e₄,);

степень вершины x₄: 6

(ребра е₇, е₈, e₉, дуги e₆, e₁₀, e₁₁);

степень вершины x₅: 3

(ребро e₉, дуга e₁₀, дуга e₁₁).

Р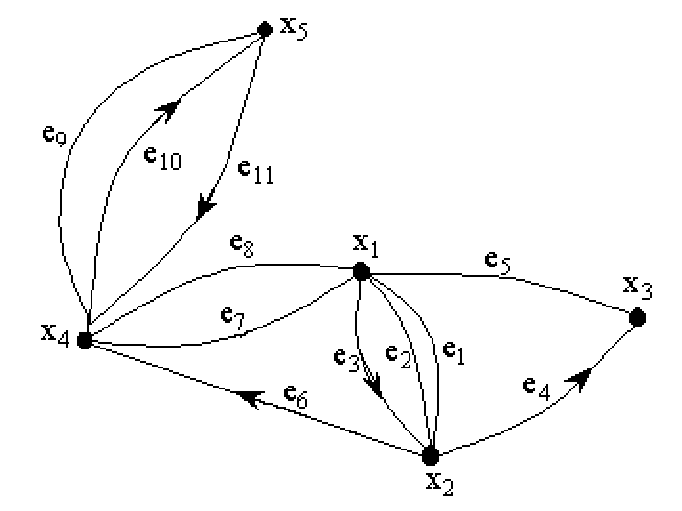исунок 20.2

В неорграфе степень вершины равна числу инцидентных ей ребер, а сумма степеней вершин равна удвоенному числу его ребер

.

Пример, подтверждающий справедливость этой формулы, показан на рис. 20.3.

Рисунок 20.3

Если degv_i= 0 , то эта вершина изолированная.

Если degv_i= 1 , то эта вершина висячая.

Для орграфа вводятся понятия полустепени исхода (deg⁺) и полустепени захода (deg^–) вершины, что соответствует числу выходящих и входящих дуг соответственно.

Для орграфа, показанного на рис. 20.4,

Рисунок 20.4

полустепень исхода вершины a: 2 (две выходящие дуги: 1, 2),

полустепень захода вершины a: 1 (одна заходящая дуга 10),

полустепень исхода вершины b: 1,

полустепень захода вершины b: 2

полустепень исхода вершины c: 2,

полустепень захода вершины c: 0,

полустепень исхода вершины d: 0,

полустепень захода вершины d: 2,

полустепень исхода вершины e: 1,

полустепень захода вершины e: 3,

полустепень исхода вершины f: 3,

полустепень захода вершины f: 0,

полустепень исхода вершины g: 1,

полустепень захода вершины g: 2.

Для орграфа и.

Если deg^–v_i= 0 , то эта вершина – источник.

Если deg⁺v_i= 0, то эта вершина тупиковая – сток.

Если граф имеет вершины одинаковой степени (полустепени исхода и захода), то его называют регулярным.

Вершины графа G(3,6)x₁,x₂,x₃(рис. 20.5) имеют одинаковую степень, равную 4, следовательно,G– регулярный граф.

Регулярный граф, в котором каждая пара смежных вершин имеет одинаковое число общих соседей и каждая пара несмежных вершин имеет свое одинаковое число общих соседей, называют сильно регулярным графом.

У графа, показанного на рис. 20.6, имеем

Смежные вершины Несмежные вершины

x₁иx₂: 2 общих соседа:x₄иx₃ х₁их₃: 2 общих соседа:x₂иx₄

x₁иx₄: 2 общих соседа:x₂иx₃ х₂их₄: 2 общих соседа:x₁иx₃

x₄иx₃: 2 общих соседа:x₁иx₂ x₂иx₃: 2 общих соседа:x₄иx₁

Одинаковое число общих Одинаковое число общих

соседей: 2. соседей: 2.

У смежных вершин и у несмежных вершин одинаковое число общих соседей по 2, следовательно, граф сильно регулярный..

Рисунок 20.5

Рисунок 20.6