19 Лекция № 18. Маршруты, достижимость, связность

Продолжительность:2 часа (90 мин.)

19.1 Ключевые вопросы

19 Лекция № 18. Маршруты, достижимость, связность 1

19.1 Ключевые вопросы 1

19.2 Текст лекции 1

19.2.1 Маршруты, связность, достижимость 1

19.2.2 Вопросы для контроля к п. 19.2.1 4

19.2.3 Метрические характеристики графа 4

19.2.4 Обхват и окружение графа 6

19.2.5 Вопросы для контроля к п. 19.2.3 и п. 19.2.4 6

19.2.6 Маршруты и циклы 7

1. Есть ли в графе маршруты длины k? 7

2. Сколько маршрутов длины k имеется в графе? 7

3. Какие маршруты длины k имеются в графе? 7

19.2.7 Вопросы для контроля к п. 19.2.6 9

19.2.8 Кратчайший маршрут во взвешенном связном графе 10

1. Волновой алгоритм 10

19.2.9 вопросы для контроля к п. 19.2.8 12

19.2 Текст лекции

19.2.1 Маршруты, связность, достижимость

Маршрутом в графе называют связную чередующуюся последовательность вершин и ребер (дуг), которая начинается и заканчивается вершиной, причем каждая соседняя пара – вершина и ребро (дуга), инцидентны друг другу.

Маршрут можно указать также перечислением вершин или ребер (дуг). Каждая пара соседних вершин или ребер (дуг) в таком представлении должны быть смежными.

В графе рис. 19.1 маршрут из точки “a” в точку “b” (а– начальная вершина,b– конечная вершина): последовательность вершинаa, дугаe₇, вершинаd, дугаe₆, вершинаe, дугаe₅, вершинаc, реброe₃, вершинаb.

Рисунок 19.1

Число ребер (дуг) в маршруте называется его длиной.

Маршрут называется цепью, если все его ребра (дуги) различны и простой цепью, если все его вершины различны.

Ориентированную цепь (цепь, состоящую только из дуг, имеющих одинаковое направление) в орграфе называют путем.

Замкнутую цепь называют циклом, если ее длина >2. Цикл называется простым, если все его вершины различны.

Замкнутый путь называют контуром, если его длина >2. Контур называется простым, если все его вершины различны.

В графе на рис. 19.2 маршрут b–e₁–c–e₂–d–e₅–bявляется замкнутым и его вершины (b,c,d) и ребра (e₁,e₂,e₅) различны, а длина маршрута равна 3, следовательно, данный маршрут можно назвать простым циклом.

Рисунок 19.2

Неорграф, в котором, перемещаясь от вершины к вершине по ребрам, можно попасть в каждую вершину, называется связным. В противном случае граф называется несвязным.

Граф G₁(4,5) на рис. 19.3 связный. Он имеет одну компоненту связности. Несвязный графG₂(6,4) на рис. 19.3 состоит из двух компонент связности.

Р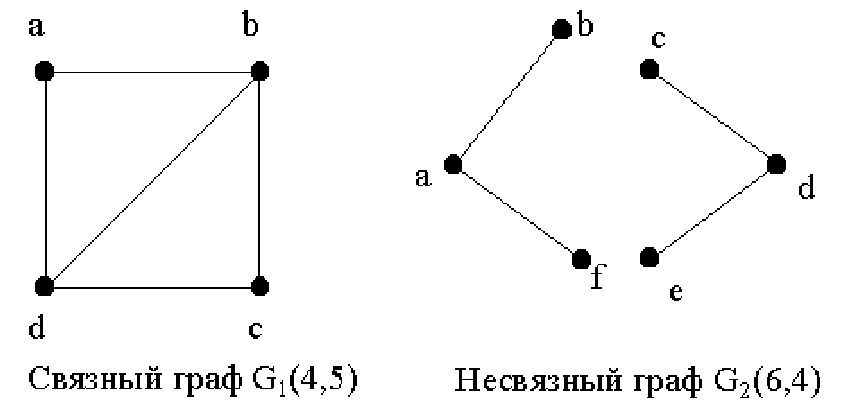исунок 19.3

Орграф связен, если связен неорграф, полученный из него заменой дуг на ребра.

Орграф называется сильно связным, если любые его вершины взаимно достижимы. Вершина yдостижима из вершиныx, если имеется путь отx доy.

Заметим, связный неорграф всегда сильно связен.

Связный орграф слабо связен, если в нем существуют пары вершин с односторонней связью. Примеры сильно связного и слабо связного графов показаны на рис. 19.4.

Вершинной связностью графа называется наименьшее число вершин, удаление которых приводит к несвязному графу или нуль–графу, т.е. графу из одних вершин.

Рисунок 19.4

Вершинная связность графа G(7,7) рис. 19.5 для получения нуль графа равна 2 (результат удаления вершинcиeпоказан на рис. 19.6, а).

Рисунок 19.5

Вершинная связность графа G(7,7) для получения несвязного графа равна 1 (результат удаления вершиныcпоказан на рис. 19.6, б).

Р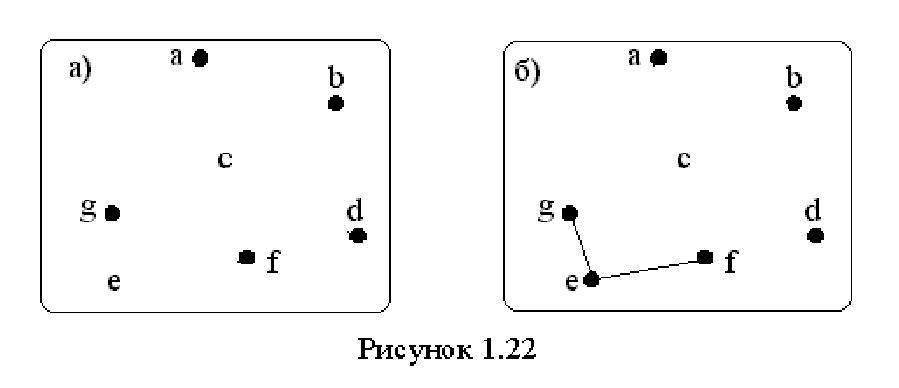исунок 19.6

Реберная (дуговая) связность определяется как наименьшее число ребер (дуг), удаление которых приводит к несвязному или нуль графу. Реберная связность графа G(4,6) показана на рис. 19.7.

Вершина графа, удаление которой увеличивает число компонент связности, называется точкой сочленения, ребро с таким же свойством называется мостом.

На рис. 19.8 показан граф, имеющий мост и три точки сочленения:

вершины x₃,x₄,x₆– точки сочленения, реброx₃,x₄– мост.

Рисунок 19.8