2 - Булева алгебра / Лекция 14 Синтез и Ан

15 Лекция № 14. Синтез и анализ логических схем

Продолжительность: 2 часа (90 мин.)

15.1 Ключевые вопросы

15 Лекция № 14. Синтез и анализ логических схем 1

15.1 Ключевые вопросы 1

15.2 Текст лекции 1

15.2.1 Синтез логических схем 1

15.2.1.1 Схемы на переключателях, диодах и транзисторах 1

15.2.1.2 Схемы на логических элементах 3

15.2.2 Анализ схем 6

15.2.3 Оценка качества схем 6

15.2.4 Вопросы для контроля 8

15.2 Текст лекции

15.2.1 Синтез логических схем

Порядок действий разработчика при синтезе логической схемы таков:

– Слово – Таблица истинности – Формула – Схема.

15.2.1.1 Схемы на переключателях, диодах и транзисторах

логические функции можно реализовывать на элементах различной физической природы. На рис. 15.1,а показаны примеры логических (переключательных) схем на контактах тумблеров или реле, а на рис. 15.1,б и рис. 15.1,в показаны схемы на диодах и транзисторах, реализующие типовые логические функции.

Рисунок 15.1,а – Реализация констант 0, 1, функций

И, ИЛИ, НЕ и на переключателях

Дадим некоторые пояснения к рис 15.1,а.

Контакт, соответствующий логической переменной x, называется замыкающим (на рис. 15.1,а обозначен как x_з). Он замыкается и пропускает ток при x = 1 и размыкается при x = 0.

Контакт, соответствующий логической переменной с отрицанием , называется размыкающим (на рис. 9,а обозначен как x_р). при x = 0 он замкнут и пропускает ток, а при x = 1 размыкается (см. также реализацию функции НЕ).

Константы «0» и «1» представляются постоянно разомкнутым и постоянно замкнутым контактами.

Таким образом, значению 1 соответствует состояние контакта «ток проходит», а значению 0 – «ток не проходит». Функции x₁x₂ соответствует последовательное соединение контактов, а функции x₁x₂ – параллельное соединение контактов (см. рис. 15.1,а).

Положения контактов, указанные на рис. 15.1,а, соответствуют нулевым значениям переменных.

Рисунок 15.1,б – Реализация логических функций на диодах

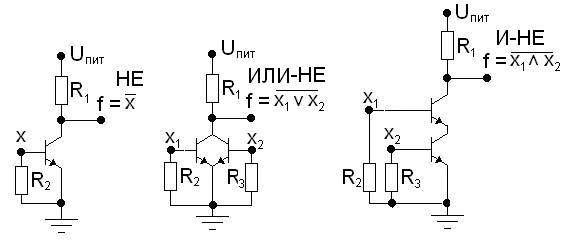
Рисунок 15.1,в – Реализация логических функций на транзисторах

На рис. 15.1,б и рис. 15.1,в даны самые простые варианты логических элементов на диодах и транзисторах. Главное – эти элементы функционируют в соответствии с таблицами истинности логических функций, имеющих те же имена.

Типовые схемы на полупроводниковых элементах принято обозначать в виде условных графических обозначений элементов, показанных в табл. 15.1.

Таблица 15.1
Отечественное обозначение	Функция	Зарубежное обозначение
	НЕ
	ИЛИ
	И
	ИЛИ – НЕ
	И – НЕ
	Исключающее ИЛИ
	Равнозначность

15.2.1.2 Схемы на логических элементах

На рис. 15.2 показана схема, реализующая мажоритарную функцию

,

полученную по табл. 12.1 после минимизации.

Построена она следующим образом.

Считаем, что входные переменные a, b, c имеются.

Рисуем три элемента И на два входа (это элементы с номерами 1, 2, 3) для реализации произведений ab, ac, bc. Подключаем к этим элементам входные переменные согласно формуле.

Рисуем элемент ИЛИ на три входа (элемент 4) и подключаем к нему выходы элементов И. На выходе элемента ИЛИ будем иметь функцию f.

На этом же рисунке показано условное обозначение этой схемы в виде одного элемента 3 – 2И – 3ИЛИ.

Рисунок 15.2 – Реализация мажоритарной функции

на логических элементах

Рассмотрим реализацию еще одной функции.

Пусть имеем функцию .

Реализуем ее на логических элементах, являющихся реализацией различных логических базисов (напомним: логический базис – это функционально полная система логических функций).

а) Реализация функции на элементах И, ИЛИ, НЕ

Порядок действий здесь следующий.

1. Получаем инверсии (1) и (2).

2. Получаем произведения с = a (3) и d = b (4).

3. Получаем сумму (5).

В скобках показаны номера элементов, реализующих операции.

Результат показан на рис. 15.3.

Рисунок 15.3 – Реализация функции

на элементах И, ИЛИ, НЕ

б) Реализация функции на элементах И–НЕ

Для использования этого базиса необходимо преобразовать функцию: взять двойное отрицание и, применив теорему де Моргана, получить выражение, удобное для реализации

(Вверху показаны шаги преобразования формулы, а в последней формуле цифрами указаны номера элементов, реализующих соответствующие ее части.)

1. Берем двойное отрицание (функция не изменяется).

2. Применяем закон де Моргана.

При создании схемы сначала получаем инверсии (1) и (2), затем реализуем с = (3) и d = (4), и, наконец, (5) (в скобках указаны номера элементов, реализующих функции, см. рис. 15.4).

Рисунок 15.4 – Реализация функции

на элементах И–НЕ

в) Реализация функции на элементах ИЛИ–НЕ

Здесь действия аналогичны действиям предыдущего пункта с тем отличием, что двойное отрицание сначала выполняется над частями выражения, а затем и над всем выражением

Реализация схемы показана на рис. 15.5.

Рисунок 15.5 – Реализация функции

на элементах ИЛИ–НЕ

Другой вариант получается, если исходную формулу представить в КНФ

Этот вариант реализован схемой, показанной на рис. 15.6.

Рисунок 15.6 – Реализация на элементах ИЛИ–НЕ функции ,

представленной в конъюнктивной форме

15.2.2 Анализ схем

Порядок действий исследователя при анализе логической схемы таков:

– Схема – Формула – Таблица истинности – Слово.

Итак, дана схема (рис. 15.6). Требуется провести ее анализ.

шаг 1: Обозначить выводы всех элементов именами (показаны на схеме).

шаг 2: Для каждого элемента, записать реализованную им функцию:

1. ; ();

2. ; ();

3. ;

4. ;

5. .

Шаг 3:

Решить систему уравнений и получить y = f(a, b).

Решаем систему логических уравнений методом подстановки с применением законов булевой алгебры

Задание: Проведите самостоятельно анализ схемы, показанной на рис. 15.7.

Рисунок 15.7 – Схема для самостоятельного анализа

15.2.3 Оценка качества схем

Качество схемы оценивается ее сложностью и задержкой сигнала в самой длинной цепочке элементов.

Сложность: C =;

M – количество элементов в схеме;

N_i – количество выводов у i–го элемента.

Задержка сигналов: T = ,

j – индексы элементов самой длинной цепи;

– задержка j–го элемента.

Оценим качество схем, показанных на рис. 15.3, рис. 15.4, рис. 15.5, рис. 15.6 и рис.15.7, приняв, что задержки сигнала у всех элементов одинаковы и равны .

Для схемы рис. 15.3 получаем С = 33 + 22 = 13; Т = 3 .

Для схемы рис. 15.4 получаем С = 35 = 15; Т = 3 .

Для схемы рис. 15.5 получаем С = 36 = 18; Т = 4 .

Для схемы рис. 15.6 получаем С = 35 = 15; Т = 3 .

Для схемы рис. 15.7 получаем С = 34 = 12; Т = 3 .

Пример показывает, что функции в ДНФ выгоднее реализовывать на элементах И–НЕ, а функции в КНФ на элементах ИЛИ–НЕ.

Довольно часто приходится сталкиваться с задачей реализации логических функций при ограничении на число входов элементов, например, имеем элементы И на 2 входа, а надо реализовать И на 6 входов. В таком случае, используя ассоциативный закон, разбиваем функцию на части по два входа. Здесь возможны варианты:

Вариант 1 .

Реализация этого варианта показана на рис. 15.8

Рисунок 15.8 – Вариант 1 реализации функции 6И на элементах 2И

Вариант 2 .

Реализация этого варианта показана на рис. 15.9.

По сложности оба эти варианта одинаковы

С = 3 5 = 15,

а по быстродействию разные:

максимальная задержка

для варианта 1 T₁ = 5τ ,

для варианта 2 T₂ = 3τ .

Рисунок 15.9 – Вариант 2 реализации функции 6И на элементах 2И

15.2.4 Вопросы для контроля

1. Какова последовательность действий в процессе создания и анализа схемы, реализующей логическую функцию?

2. Как реализуются логические функции с помощью контактов переключателей и реле? Приведите примеры.

3. Приведите примеры реализации логических функций на диодах и транзисторах.

4. Приведите условные графические обозначения типовых логических элементов.

5. Какова последовательность действий при реализации логической функции на элементах И, ИЛИ, НЕ?

6. Какова последовательность действий при реализации логической функции на элементах И–НЕ?

7. Какова последовательность действий при реализации логической функции на элементах ИЛИ–НЕ?

8. Какова последовательность действий при реализации логической функции, если имеется ограничение на число входов элементов?

9. Как проводится анализ комбинационной логической схемы?

10. Как оценивается качество логических схем?