
численные методы
.docx1.Что такое Численные методы?
Численные методы – математическая дисциплина, изучающая методы приближённого решения математических задач, сводящиеся к выполнению конечного числа элементарных операций над числами. Численные методы сводят решение математических задач, которые могут быть проведены как в ручную, так и с помощью ЭВМ
2.Перечислите типичные задачи численных методов.
1)Решение уравнений
2)Численное интегрирование
3)Решение дифференциальных уравнений
3.Что такое абсолютная и относительная погрешность вычислений.
Если ![]() -
точное значение некоторой величины,
а
-
точное значение некоторой величины,
а ![]() -
известное приближение к нему, то
абсолютной погрешностью приближения
-
известное приближение к нему, то
абсолютной погрешностью приближения ![]() называют
обычно некоторую величину
называют
обычно некоторую величину ![]() ,
про которую известно, что она удовлетворяет
неравенству:
,
про которую известно, что она удовлетворяет
неравенству:
![]()
Относительной
погрешностью называют некоторую
величину ![]() ,
про которую известно, что она
удовлетворяет неравенству:
,
про которую известно, что она
удовлетворяет неравенству:

Относительную погрешность часто выражают в процентах. Она дает более точное представление о величине ошибки, содержащейся в некоторой величине.
4. Что такое интерполяция функции?
Интерполяцией функции f(x) называется замена ее функцией F(x) определенного класса, совпадающей с f(x) в точках xk. При этом точки xk называются узлами интерполяции.
Геометрически интерполяция заключается в проведении графика интерполирующей функции F(x) через узловую точку: (x0, F(x0)), (x1, F(x1)),…, (xn, F(xn))
5. Прямой метод интерполяции.
Пусть в точка х0, х1 известны значения функций у(х): у0, у1, .., уn. Требуется построить многочлен F(х) такой что
F(x0) = y0
F(x1) = y1
F(xn) = yn Степень многочлена F(x) не должна быть выше n
F(x) имеет вид:
F(x) = a0 + a1x + a2x^2 +…+ anx^n
a0 + a1x0 + a2x0^2 +…+ anx0^n = y0
a0 + a1x1 + a2x1^2 +…+ anx1^n = y1
a0 + a1xn + a2xn^2 +…+ anxn^n = yn
неизвестный а1,..,an
Получим систему из n-линейных уравнений с n-неизвестными.
Такая система имеет единственное решение, т.е. коэффициенты многочлена а0, а1, …, an могут быть найдены единственным образом.
6. Понятие об интерполяционном многочлене Лагранжа. Достоинства и недостатки.
Основная идея этого метода состоит в том, чтобы, прежде всего найти многочлен, который принимает значение 1 в одной узловой точке и 0 во всех других. Он имеет вид:
Ln(х)
=


 Т.
к.
Т.
к.
 при i
= j,
то
при i
= j,
то
 – корень многочлена
– корень многочлена
 .
Тогда
.
Тогда
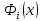 делится на (х -
делится на (х -
 )
при i
= j.
Таким образом многочлен
)
при i
= j.
Таким образом многочлен
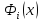 может быть
может быть
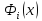 = Const
*
= Const
*

Найдём const в этом многочлене:

 ,
тогда
,
тогда

 = 1
= 1
 Const
=
Const
=


 =
=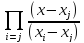
 подставим
в Ln(х)
подставим
в Ln(х)
 Ln(х)
=
Ln(х)
=
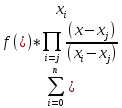 или
или
Ln(х)
=
 *
*

Достоинство – метод наиболее прост в понимании и организации вычислительного процесса, относится к числу итерационных методов и имеет наибольшую точность интерполяции, использование многочленов невысокого порядка и вследствие этого малым накоплением погрешностей в процессе вычислений.
Недостаток метода – при увеличении числа узлов и соответственно степени интерполяционный многочлен Лагранжа требуется строить заново, медленная скорость сходимости, что приводит к значительным затратам машинного времени. 7. Интерполяционный многочлен Ньютона. Достоинства и недостатки.
Можно построить интерполяционный многочлен степени n в виде
 Многочлен
Многочлен ![]() должен
проходить через узлы интерполирования,
т.е.
должен
проходить через узлы интерполирования,
т.е.
![]() =
yi =
f(xi)
(i = 1,2, ………..n).
=
yi =
f(xi)
(i = 1,2, ………..n).
Причём
х
= х0 ; ![]() =
y0 =
а0 .
Отсюда а0 =
y0
.
х
= х1;
=
y0 =
а0 .
Отсюда а0 =
y0
.
х
= х1; ![]()
![]() =
y0 +
а1h,
где
=
y0 +
а1h,
где ![]()
Аналогично можно получить значения и остальных коэффициентов многочлена
![]() ;
; ![]() ………………….
………………….![]() .
.
![]() ,
, ![]() ,………….
,………….![]() -
конечные разности до n-ого порядка.
В
общем случае конечные разности можно
представить
-
конечные разности до n-ого порядка.
В
общем случае конечные разности можно
представить
![]() (i
= 1,2, ………..n-1).
(i
= 1,2, ………..n-1).
![]() =
= ![]() (i
= 1,2, ………..n-1) и разность
порядка к
…………………………………….
(i
= 1,2, ………..n-1) и разность
порядка к
…………………………………….
![]() (i
= 1,2, ………..n-1).
(i
= 1,2, ………..n-1).
Если в интерполяционный многочлен подставить значения коэффициентов, то будет получен первый интерполяционный многочлен Ньютона
![]()
Достоинство: она удобна тем, что число используемых узлов может быть легко увеличено или уменьшено без повторения всего вычисления.
Недостаток: К недостатку формулы Ньютона можно отнести то, что при вычислениях в таблице с постоянным шагом при увеличении количества узлов не всегда удается добиться повышения точности вычислений.
8. Что такое конечные разности?
Конечная разность — математический термин, широко применяющийся в методах вычисления при интерполировании.
Рассмотрим
интерполяционную задачу для функции ![]() :
:
![]()
где ![]() -
шаг интерполяции
-
шаг интерполяции
Конечной
разностью 1-го порядка называют
разность между двумя соседними
значениями ![]() в
узлах интерполяции, то есть
в
узлах интерполяции, то есть
![]()
Конечной разностью 2-го порядка называют разность между двумя соседними конечными разностями 1-го порядка, то есть
![]()
Конечной
разностью порядка ![]() (для
(для ![]() )
называют разность между двумя соседними
конечными разностями порядка
)
называют разность между двумя соседними
конечными разностями порядка ![]() ,
то есть
,
то есть
![]()
9. Понятие об интерполировании сплайнами.
Spline – планка, рейка.
Сплайн – лекало, гибкая металлическая линейка.
Сплайн - функция, область определения которой разбита на конечное число отрезков, на каждом из которых сплайн совпадает с некоторым алгебраическим многочленом. Т.о. сплайн – это функция, собранная из различных функций одного вида.
Чаще всего используются кубические сплайны. В сплайне фрагменты стыкуются гладко.
 (
( )
=
)
=
 (
( )
) (
( )
=
)
=
 (
(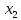 )
)
 (
( )
=
)
=
 (
( )
)
 (
(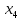 )
=
)
=
 (
( )
– это условие совпадения кусков в
граничащих точках
)
– это условие совпадения кусков в
граничащих точках
10. Что такое аппроксимация?
Аппроксимация (от лат. approximo — приближаюсь), замена одних математических объектов другими, в том или ином смысле близкими к исходным. Аппроксимация позволяет исследовать числовые характеристики и качественные свойства объекта, сводя задачу к изучению более простых или более удобных объектов (например, таких, характеристики которых легко вычисляются или свойства которых уже известны).
11. Два этапа численного решения уравнений: отделение и уточнение корней.


12. Метод половинного деления или дихотомии.
Пусть дано уравнение f(x) = 0, имеющее на отрезке [a,b] один корень. В качестве начального приближения корня х0 рассмотрим середину отрезка [a,b] : х0 = (b + a) / 2

13. Методы численного интегрирования. Их связь с определением определённого интеграла.


14. Описание методов прямоугольников.


Формула левых прямоугольников.

Формула правых прямоугольников.


Формула средних прямоугольников.

15. Метод трапеций.


16. Метод парабол.




17. Сравнение методов численного интегрирования.
Методы левых и правых прямоугольников являются методами первого порядка точности по степени h

Соответственно метод средних прямоугольников и метод трапеций второго порядка точности

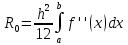
Сравнив методы прямоугольников и трапеций с методом Симпсона, отметим, что последний обладает более высоким порядком точности – четвертым.

