Задачи Тер.вер
.docx1. Закон распределения дискретной двумерной случайной величины (ξ,η) задан таблицей.
|
η \ ξ |
1 |
2 |
5 |
|
-1 |
0,15 |
0,05 |
0,3 |
|
0 |
0,3 |
0,05 |
0,15 |
Найти:
1. Вероятность события Р(1 ≤ ξ < 6; η <0).
2. Вероятность события Р(0 ≤ ξ < 5; -1≤η <1).
3. Условный закон распределения компоненты ξ при условии, что η=0 и условное математическое ожидание М(ξ/η=0); сделать вывод - зависимы или нет ξ и η.
4. Условный закон распределения компоненты η при условии, что ξ=2 и условное математическое ожидание М(η/ξ=2).
2. Закон распределения дискретной двумерной случайной величины (ξ,η) задан таблицей.
|
η \ ξ |
-1 |
0 |
1 |
|
3 |
0.1 |
0.3 |
0.25 |
|
6 |
0.25 |
0.05 |
0.05 |
Найти:
1. Вероятность события Р(ξ < 1; 0 ≤ η <6).
2. Вероятность события Р(-1 ≤ ξ < 2; 6≤η < 8).
3. Условный закон распределения компоненты ξ при условии, что η=3 и условное математическое ожидание М(ξ/η=3); сделать вывод - зависимы или нет ξ и η.
4. Условный закон распределения компоненты η при условии, что ξ=1 и условное математическое ожидание М(η/ξ=1).
3. Для
двумерной случайной величины (ξ,η)
известно следующее: D(ξ)=36,
M(η)=5, M(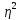 )=36,
)=36,
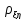 =0,6.
Найти D(2ξ-4η+7).
=0,6.
Найти D(2ξ-4η+7).
4. Для
двумерной случайной величины (ξ,η)
известно следующее: D(2ξ-4)=16,
M(η)=3, M(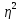 )=13,
)=13,
 =0,5.
Найти cov(3ξ,5η).
=0,5.
Найти cov(3ξ,5η).
5. Случайная выборка из генеральной совокупности представлена в виде вариационного ряда:
|
X |
-2 |
-1 |
0 |
1 |
3 |
5 |
6 |
|
|
3 |
2 |
4 |
6 |
3 |
1 |
1 |
Считая признак Х распределенным нормально, выполнить следующее:
1. Определить по выборке исправленную дисперсию.
2. С надежностью 0,002 построить доверительный интервал для математического ожидания признака Х.
3. С надежностью 0,1 построить доверительный интервал для дисперсии признака Х.
4. С надежностью 0,01 проверить гипотезу
о том, что математическое ожидание
признака Х равно 1 при альтернативной
гипотезе: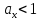 .
.
5. С надежностью 0,025 проверить гипотезу
о том, что дисперсия признака Х равна
4,3 при альтернативной гипотезе:
 >4,3.
>4,3.
6. Случайная выборка из генеральной совокупности представлена в виде вариационного ряда:
|
X |
2 |
4 |
6 |
8 |
10 |
|
|
1 |
3 |
7 |
4 |
1 |
Считая признак Х распределенным нормально, выполнить следующее:
1. Определить по выборке исправленную дисперсию.
2. С надежностью 0,1 построить доверительный интервал для математического ожидания признака Х.
3. С надежностью 0,02 построить доверительный интервал для дисперсии признака Х.
4. С надежностью 0,01 проверить гипотезу
о том, что математическое ожидание
признака Х равно 7,3 при альтернативной
гипотезе:
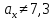 .
.
5. С надежностью 0,05 проверить гипотезу
о том, что дисперсия признака Х равна
4,1 при альтернативной гипотезе:
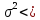 4,1.
4,1.
7. По итогам
исследования выборки, содержащей 22 пары
значений признаков (Х, Y),
получены следующие оценки числовых
характеристик: для признака Х:
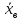 =3,
=3,
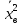 =25;
для признака Y:
=25;
для признака Y:
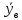 =8,
=8,
 =68;
а так же известно:
=68;
а так же известно:
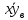 =20,4
=20,4
Выполнить следующее:
1. Определить выборочный коэффициент корреляции, сделать вывод о виде связи между признаками Х и Y.
2. Проверить гипотезу о значимости полученного коэффициента корреляции при уровне значимости 0,01.
8. По итогам
исследования выборки, содержащей 27 пар
значений признаков (Х, Y),
получены следующие оценки числовых
характеристик: для признака Х:
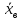 =7,
=7,
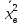 =50;
для признака Y:
=50;
для признака Y:
 =4,
=4,
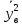 =20;
а так же известно:
=20;
а так же известно:
 =1
=1
Выполнить следующее:
1. Определить выборочный коэффициент корреляции, сделать вывод о виде связи между признаками Х и Y.
2. Проверить гипотезу о значимости полученного коэффициента корреляции при уровне значимости 0,02.
9. Исследуется
зависимость признака Y
от признака Х. Получены статистические
данные по выборке объема 21 значений Y
в виде набора групповых средних признака
Y, вычисленных для 5 значений
признака Х:
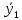 =81,
=81,
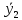 =80,5,
=80,5,
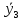 =81,8,
=81,8,
 =81,3,
=81,3,
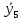 =82.
Объемы групп равны соответственно:
=82.
Объемы групп равны соответственно:
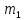 =7,
=7,
 =3,
=3,
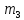 =5,
=5,
 =4,
=4,
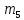 =2.
Кроме того, дано:
=2.
Кроме того, дано:
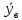 =81,5,
=81,5,
 (Y)=0,71.
(Y)=0,71.
Выполнить следующее:
1. Определить
межгрупповую дисперсию Y
и корреляционное отношение
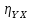 .
В ответе указать
.
В ответе указать
 .
.
2. Проверить
гипотезу о значимости
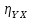 при уровне значимости 0,05.
при уровне значимости 0,05.
10.
Исследуется зависимость признака Y
от признака Х. Получены статистические
данные по выборке объема 15 значений Y
в виде набора групповых средних признака
Y, вычисленных для 35
значений признака Х:
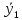 =11,
=11,
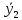 =12,3,
=12,3,
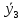 =10,5.
Объемы групп равны соответственно:
=10,5.
Объемы групп равны соответственно:
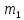 =3,
=3,
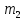 =7,
=7,
 =5.
Кроме того, дано:
=5.
Кроме того, дано:
 =11,5,
=11,5,
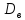 (Y)=7,58.
(Y)=7,58.
Выполнить следующее:
1. Определить
межгрупповую дисперсию Y
и корреляционное отношение
 .
В ответе указать
.
В ответе указать
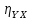 .
.
2. Проверить
гипотезу о значимости
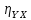 при уровне значимости 0,01.
при уровне значимости 0,01.