3.6. Связность графа

Неориентированный граф называется связным, если каждая пара различных вершин может быть соединена по крайней мере одной цепью.

Ориентированный граф называется сильно связным, если для любых двух его вершин x_i и x_j существует хотя бы один путь, соединяющий x_i с x_j.

Ориентированный граф называется односторонне связным, если для любых двух его вершин по крайней мере одна достижима из другой.

Компонентой связности неориентированного графа называется его связный подграф, не являющийся собственным подграфом никакого другого связного подграфа данного графа (максимально связный подграф).

Компонентой сильной связности ориентированного графа называется его сильно связный подграф, не являющийся собственным подграфом никакого другого сильно связного подграфа данного графа (максимально сильно связный подграф).

Компонентой одностронней связности неориентированного графа называется его односторонне связный подграф, не являющийся собственным подграфом никакого другого односторонне связного подграфа данного графа (максимально односторонне связный подграф).

Пусть G = (X, A) неориентирован­ный граф с множеством вершин X = {x₁,...,x_n}. Квадратная матрица S = (s_ij) порядка n, у которой

s_ij =

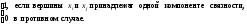
называется матрицей связности графа G.

Для ориентированного графа квадратная матрица T = (t_ij) порядка n, у кото­рой

t_ij =

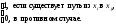
называется матрицей односторонней связности (достижимости).

Квадратная матрица S = (s_ij) порядка n, у которой

s_ij =

называется матрицей сильной связности.

Пример 3.13.

У неориентированного графа, изображенного на рис. 3.8 две компоненты связности. Первая компонента связности включает вершины x₁, x₂, x₄, x₅, а вторая состоит из одной вершины x₃.

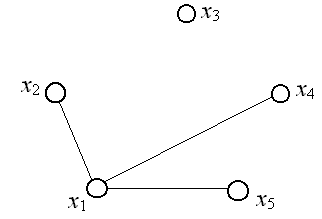
Рис.3.8

Матрица связности этого графа имеет вид:

S =

Мы видим, что 1-ая, 2-ая, 4-ая и 5-ая строки матрицы S одинаковы.

Пример 3.14.

У ориентированного графа, изображенного на рис. 3.9 две компоненты сильной связности. Первая компонента связности включает вершины x₁, x₂, x₃, x₅, а вторая состоит из одной вершины x₄. Действительно, для любой пары вершин из множества {x₁, x₂, x₃, x₅} существует хотя бы один путь, соединяющий эти вершины. Например, путь (x₁, x₂, x₅, x₃, x₁) соединяет все эти вершины. Из вершины x₄ нет пути ни в одну вершину графа.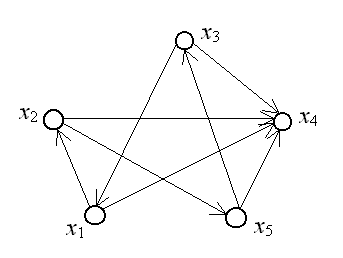

Рис. 3.9

Матрица сильной связности этого графа имеет вид:

S =

Мы видим, что 1-ая, 2-ая, 3-ая и 5-ая строки матрицы S одинаковы.

3.7. Экстремальные пути в нагруженных ориентированных графах

Ориентированный граф называется нагруженным, если дугам этого графа поставлены в соответствие веса, так что дуге (x_i,x_j) сопоставле­но некоторое число c(x_i,x_j) = c_ij, называемое длиной (или весом, или стоимостью дуги). Длиной (или весом или стоимостью) пути s, состоящего из некоторой последовательности дуг (x_i,x_j), называется число l(s), равное сумме длин дуг, входящих в этот путь, т.е.

l(s) = 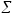c_ij,

причем суммирование ведется по всем дугам (x_i, x_j) s.

Матрица C = (c_ij) называется матрицей длин дуг или матрицей весов.

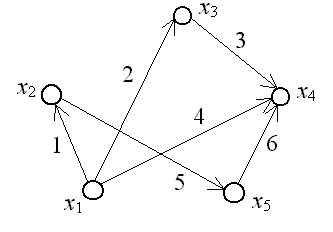
Рис. 3.10

Для графа, изображенного на рис. 3.10, матрица C имеет вид:

C =

Длина пути (x₁, x₂, x₅, x₄) равна 1 + 5 + 6 = 12.

Для ненагруженного графа введем понятие кратчайшего пути. Это путь с минимальным общим числом дуг, причем каждая дуга считается столько раз, сколько она содержится в этом пути.

Для нахождения минимального пути между двумя произвольными верши­нами для случая, когда все c_ij ³ 0 можно воспользоваться простым алгоритмом Дейкстры [2]. В общем случае задача решается с помощью ал­горитмов Флойда, Форда, Беллмана и др. [2,3,5].

Алгоритмы нахождения минимального пути могут быть использованы для поиска кратчайших путей в ориентированном графе без контуров. Для этого нужно каждой дуге приписать вес, равный единице.