Точность сау на установившемся режиме

Рассмотрим структурную схему САУ

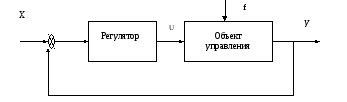
Пусть передаточная функция объекта по управляющему воздействию

Пусть передаточная функция объекта по возмущению

Пусть передаточная функция регулятора

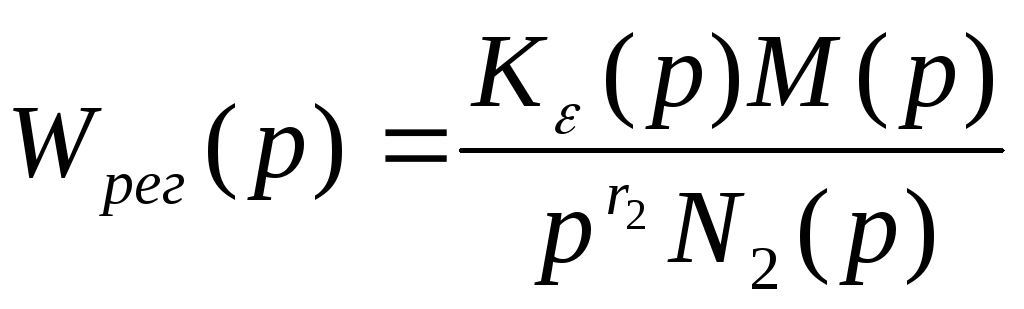
Тогда

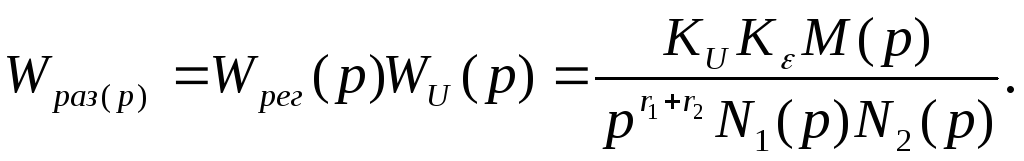
Обозначим общий коэффициент усиления

Тогда

.

Запишем управляющее воздействие

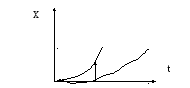
При - т.е. это постоянное воздействие

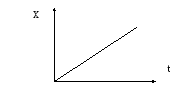
При - это линейное воздействие , т.е. воздействие, изменяющееся с постоянной скоростью, «линейка».

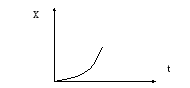
При - это парабола, воздействие, изменяющееся с постоянным ускорением, «парабола».

Для устойчивой системы можно вывести зависимость ошибки на установившемся режиме от структуры системы ( есть или нет в структуре интегрирующие звенья и сколько их) и порядка полинома управляющего и возмущающего воздействий.

Результаты сведем в таблицу.

Зависимость установившейся ошибки

по управляющему воздействию

Таблица 1

1.

2.

3.

4.

Системы, у которых - это астатические системыпорядка.

В статических системах .

Рассмотрим примеры.

Статическая система.

1. . Это - случай.

2. - это2- случай.

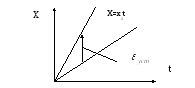
Астатическая система 1-го порядка.

1.,.. Это1-случай . .

2. Это3 случай.

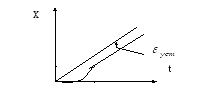
3. Это2 случай.

Таким образом, для повышения точности систем на установившемся режиме по управляющему воздействию надо увеличивать порядок астатизма и коэффициент усиления К. Но эти меры могут привести к нарушению устойчивости, для восстановления которой надо вводить дополнительные корректирующие устройства.

Ошибка системы на установившемся режиме

по возмущающему воздействию.

Возмущающие воздействия описываются также, как и управляющие воздействия:

Ошибки системы по возмущающему воздействию зависят от количества интегрирующих звеньев в регуляторе и порядка полинома воздействия.

При этом приведенные в таблице ниже соотношения определяют установившееся значение выходной величины .

Таблица 2

1. ,

2. ,

3. ,

4. ,

Системы, имеющие регулятор с астатизмом 1-го порядка при постоянном возмущении (- это1-ый случай) имеют установившееся значение

При линейно- возрастающем возмущающем воздействии (это 3-ий случай) изменяется на темменьшую величину, чем больше К.

Пример. Определить ошибку в установившемся режиме для системы

1)

2)

3)

Проверим устойчивость системы.

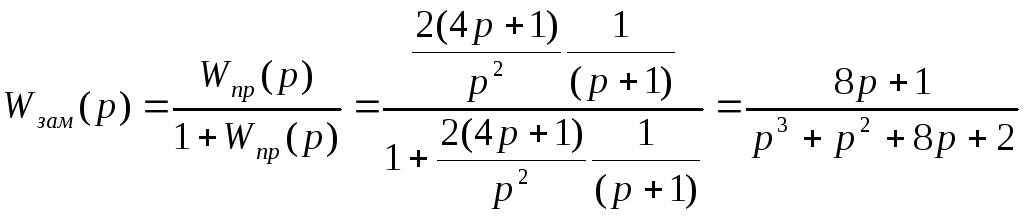
Характеристическое уравнение

По критерию устойчивости Гурвица и САУ устойчива.

1 случай Это 2 случай из таблицы 1.

2 случай Это3 случай из таблицы 1.(К=2)

3 случай Это1=ый случай из таблицы 1.

Коэффициенты ошибок

Точность САУ по управляющему воздействию можно определить по коэффициентам ошибок.

Рассмотрим САУ

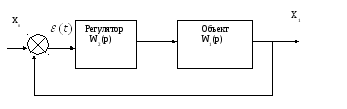
Передаточная функция замкнутой системы по ошибке

Разложим в степенной ряд Маклорена при(). Ряд Маклорена – частный случай ряда Тейлора, когда разложение идет в окрестности

Представим ряд Маклорена иначе:

Здесь С₀, С₁, С₂ …. – коэффициенты ошибок, Их физический смысл – производные передаточных функций в окрестности (), т.е. в установившемся режиме.

Пусть передаточная функция имеет вид:

.

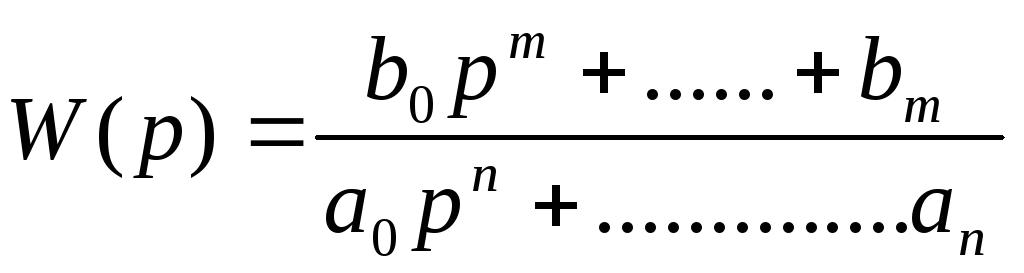Напомним, производная от дроби

=

_,

₍

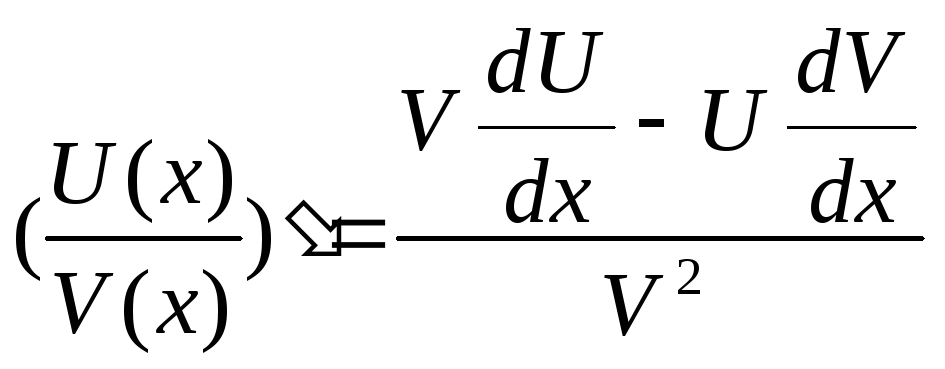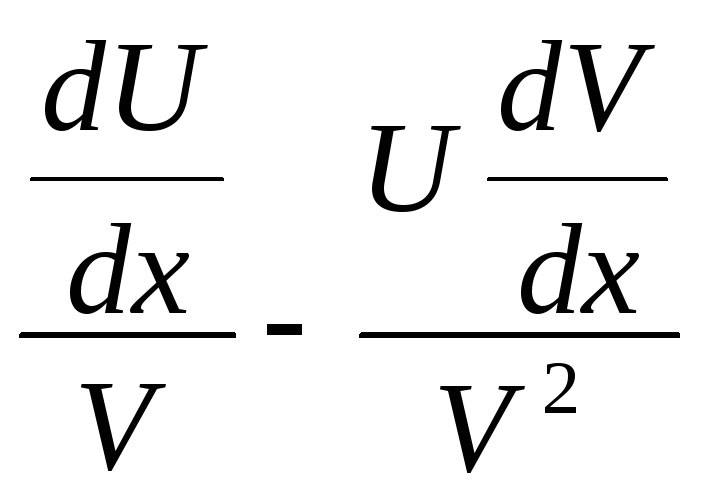
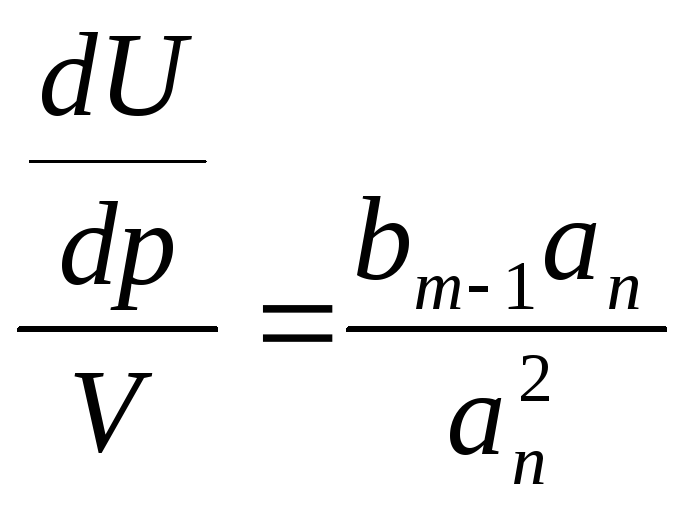
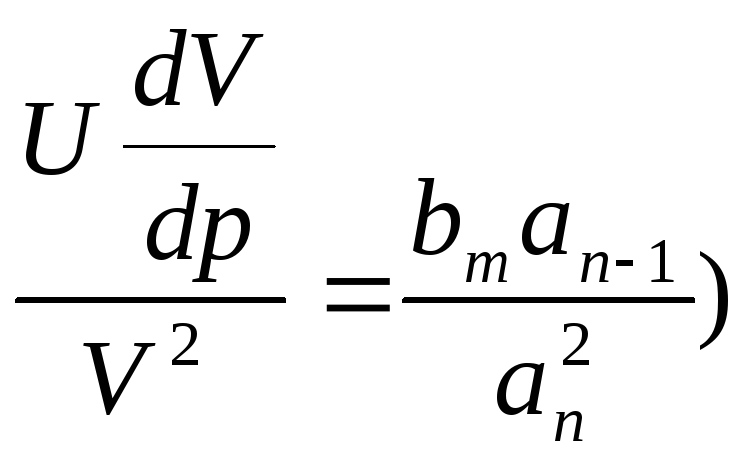
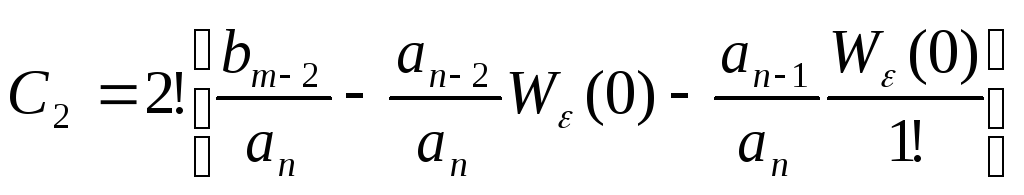
Рассмотрим систему с астатизмом первого порядка.

Пусть ,

Тогда ,

т.е.

Тогда

и т.еи нет статической ошибки.

Рассмотрим систему с астатизмом второго порядка.

Пусть ,

Тогда

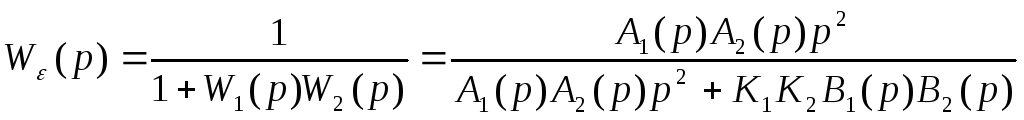
Значит, и

Следовательно , можно сделать вывод:

- статическая ошибка по управляющему воздействию при ступенчатом воздействии,

- статическая ошибка по управляющему воздействию по скорости,

- статическая ошибка по управляющему воздействию по ускорению.

Пример.

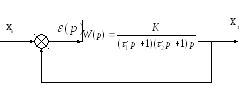
Это система с одним интегрирующим звеном. Причем не отмечено, где оно находится- в объекте или в регуляторе.

Эта система ведет себя одинаково (см. таблицу 3 случаи 2 и 3) при различных управляющих воздействиях: скачке, «линейке», «параболе».

Найдем коэффициенты ошибок и сравним их с таблицей 3.

Передаточная функция замкнутой системы по ошибке:

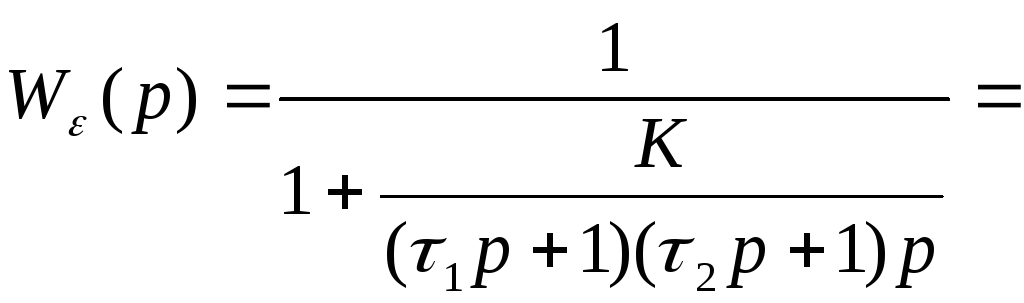
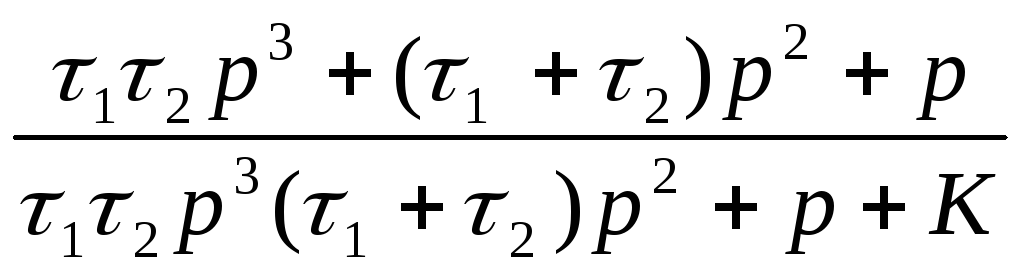
Здесь

Обозначим коэффициенты в числителе

.

Коэффициенты в знаменателе:

Тогда ошибка при скачке:

Ошибка при «линейке» (при сигнале, изменяющемся с постоянной скоростью)

Ошибка при «параболе» (при сигнале, изменяющемся с постоянным ускорением)

==

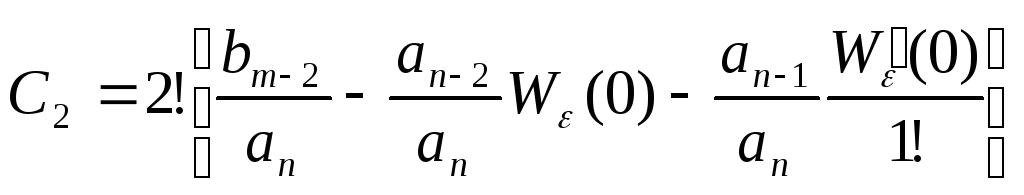Изменение ошибки во времени:

Скачок: ,

«Линейка» ,

«Парабола»

0+

При третий член- постоянная величина, а второй – стремится к бесконечности. Т.о.