12

Московская государственный университет приборостроения и информатики

Кафедра физики

Методическое пособие

для выполнения лабораторных работ по физике

Часть III

Ф.И.О. студента___________________________________________

№ группы ________________________________________________

УКП ____________________________________________________

Ф.И.О. ведущего преподавателя _____________________________

_________________________________________________________

Лаб. работа №401 РАБОТА ЗАЧТЕНА

Лаб. работа №402 РАБОТА ЗАЧТЕНА

Лаб. работа №501 РАБОТА ЗАЧТЕНА

___________________________

Порядок выполнения работ

1. Номер работы, которую студент будет выполнять на следующем занятии, назначает преподаватель, проводящий лабораторные работы.

2. Перед лабораторной работой студент должен знать ответы на контрольные вопросы, приведенные в конце работы и решить домашние задачи, относящиеся к теме работы. Студенты, не выполнившие этих требований, к лабораторной работе не допускаются.

3. Экспериментальные и расчетные данные заносятся в журнал только с разрешения ведущего преподавателя. Все предварительные расчеты выполняются на черновике. Обработка результатов измерений проводится согласно разделу “Элементарная теория оценки ошибок измерения”.

4. После выполнения работы преподаватель должен поставить отметку в журнале.

5. Студенты, не сдавшие в срок лабораторные работы, к экзамену не допускаются.

Элементарная теория оценки ошибок измерений

Целью каждой лабораторной работы является определение некоторой величины y, для которой приводится функциональное соотношение (формула), выражающая ее через одну или несколько величин

. (1)

Непосредственно в эксперименте измеряется не сама искомая величина у, а только величиныx₁, х₂, ...,х_N, которые в дальнейшем называются измерениями. Для измерения величиниспользуются приборы, реальные измерительные возможности которых ограничиваются рядом объективных причин, кроющихся в физической природе измеряемых физических величин. Так при измерении плотности с высокой точностью проявляются флуктуации числа частиц и массы в единице объема. При измерении тока – числа носителей заряда, при измерении интенсивности света – числа фотонов в световых потоках и многое другое.

Поэтому любую из измеряемых на практике физических величин можно представить в виде , где– некоторое истинное точное значение (которое полагается физически существующим) измеряемой величины, аDх– отклонение от истинного значения, обусловленное неточностями лабораторного эксперимента.

Будем считать, что все отклонения истинного значения в лабораторном эксперименте имеют статистически независимый случайный характер, поэтому при многократных повторениях одного и того же измерения значения отклоненияDхбудут иметь случайный разброс в разные от нуля стороны. Даже в результате многократных измерений величиныхнельзя точно указать истинное значение измеряемой величины, но можно указать интервал ее значений, в котором она находится с вероятностью, близкой к единице. Интервал таких значений обычно представляется в виде,

чему соответствует форма записи результатов измерений в виде , гдеx_CP– среднее значение измеряемой величиных. Оно определяется, как среднее арифметическое по всем измерениям: , гдех_i– значение величиных вi-том измерении;n– полное количество измерений.

Величина называется средней абсолютной ошибкой измеряемой величиных. Она определяется, какгде вертикальными скобками обозначен модуль разности. При записи результата измерений необходимо соблюдать следующиеправила:

1. значение абсолютной ошибки 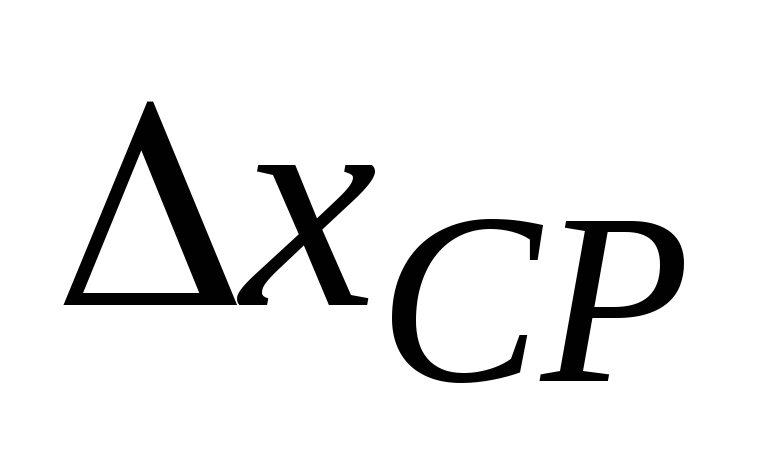необходимо округлить до двух значащих цифр, если первая из них – единица, и до одной – во всех остальных случаях;

2) при записи численного значения величины х_СР необходимо указывать столько же знаков после запятой, сколько использовано для записи. В качестве правильной записи результатов можно привести пример

1) , если, а;

2) , если, а.

Примеры неправильной записи результата измерений:

1) х = (1.11±0.01) м– нарушено правило1;

2) х = (1.11±0.013) м– нарушено правило2;

3) х = (1.11±0.0134) м– нарушено правило1;

4) х = (1.11±0.023) м– нарушено правило1.

  Класс точности измерений характеризуется как величиной абсолютных ошибок, так и относительных, которые вычисляются по формуле: .

Относительная ошибка во многом более наглядна. Например, измерения размеров дома и земного шара с точностью до одного метра совершенно несоизмеримы по величине относительных ошибок, отличающихся почти в миллион раз.

Естественный и линейно поляризованный свет. Поляризаторы

Свет – поперечная электромагнитная волна. Векторы напряженности электрического поля и индукции магнитного поляв любой момент времени взаимно перпендикулярны и колеблются перпендикулярно вектору скорости распространения волны, т.е. колеблются перпендикулярно лучу.

При взаимодействии света веществом основное действие вызывается колебаниями вектора, который в связи с этим иногда называют световым вектором .луч

Поэтому для описания закономерностей поляризации света следят

за поведением вектора . Рис.1.

Вестественном свете направление колебаний векторав плоскости, перпендикулярной лучу неупорядочено (см. рис. 1). В любой момент времени вектор напряженности

можно представить как сумму двух взаимно перпендикулярных векторов (см. рис. 2).

Поэтому естественный (неполяризованный) свет иногда Рис.2

условно обозначают так    луч (точка - вектор , стрелка -вектор).

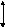
П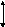оляризатор– оптическое устройство, на выходе из которого вектор напряженности имеет только одну составляющую. Эти приборы полностью или частично задерживают колебания, перпендикулярные этой составляющей. Если на вход поляризатора луч

попадает неполяризованный свет, то на выходе колебания

вектора напряженности будут иметь вид изображенный на рис.3. Рис.3

Такой свет называетсялинейно (или плоско) поляризованным. поляризатор

Плоскость, образованная вектором и лучом называетсяось поляризатора

плоскостью колебаний вектора напряженности. Прямая, лежащая в плоскости поляризатора, вдоль которой происходят колебания вектора , называетсяосью поляризатора.

В зависимости от положения оси поляризатора линейно поляризованный свет обозначается

так    или так .

Лабораторная работа 4-01