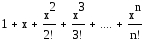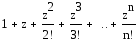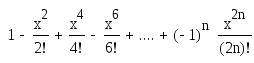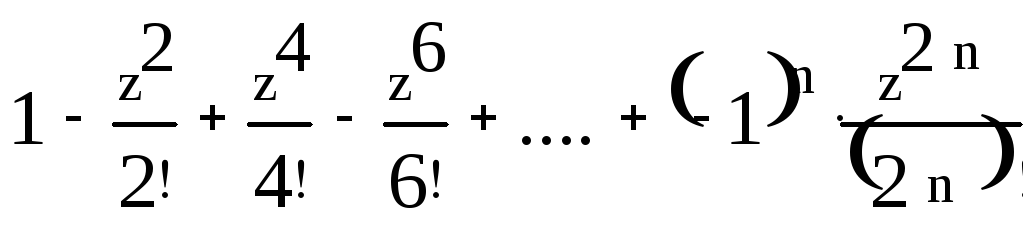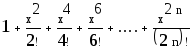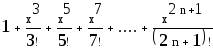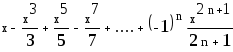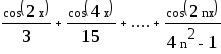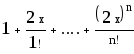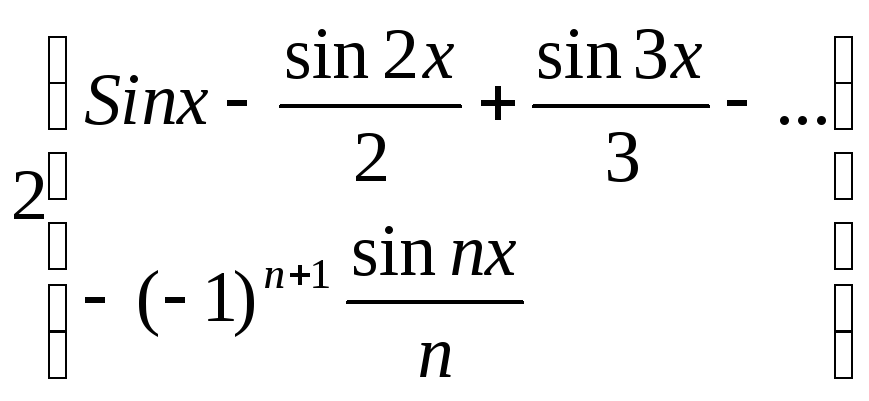Пример оформления лабораторной работы.
Постановка задачи.
Дано:
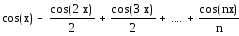
V=
- формула члена ряда.
Y= - ln|2* sin (X/2)| - точное значение.
e=10-4 – точность вычисления.
π/5 < = X < = 9π/5, ∆X= π/5
Блок-схема:
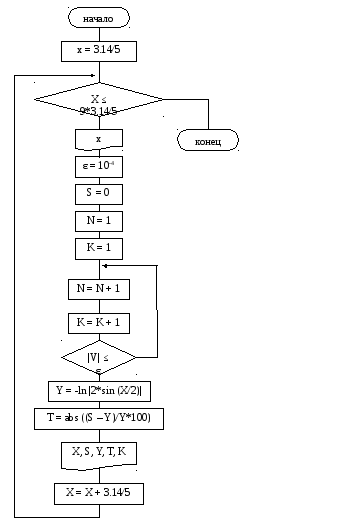
нет
да
Нет
да
Программа.
CLS
PRINT "значение переменной/сумма/точное значение функции/ошибка
расчета/ число шагов "
PRINT "X /S /Y /T /K "
e=0.0001
For X=3.14/5 to 9*3.14/5 step 3.14/5
S=0
N=1
K=0
Do
V=cos (N*X)/N
S=S+V
N=N+1
K=K+1
Loop until ABS (V) < =e
Y = -log (ABS (2*sin (X/2)))
T=ABS (S-Y) (Y*100)
Print X, S, Y, T, K
NEXT X
END
Вывод результатов программы:
|
X |
S |
Y |
T |
K |
|
0.6 1.6 2.6 3.6 4.6 5.6 |
0.4837 -0.3658 -0.6624 -0.6626 -0.3840 0.4492
|
0.48 -0.37 -0.66 -0.66 -0.39 0.44 |
0.4 2.3 0.4 0.1 0.8 1.9 |
753 55 52 192 149 175
|
В приведенном примере вычислена только сумма ряда с определенным значением параметра X, который вводится с помощью оператора input.
При выполнении варианта задания в лабораторной работе значение X меняется от X начального до X конечного с шагом dX.
Вариант для выполнения работы студент получает у преподавателя (см. задание № 1).
Задание №1
Нахождение суммы бесконечного ряда.
|
№ вар |
Сумма S |
Значения аргумента |
Условие окончания |
Функция Y(точное значение) | |
|
|
|
Xн=0.1 Xк=1 |
Шаг 0.1 |
E=10-4 |
ex |
|
|
|
Zн=0 Zк=2 |
Шаг 0.2 |
E=10-4 |
ez |
|
|
|
Xн=0.1 Xк=1 |
Шаг 0.1 |
E=10-4 |
cos (x) |
|
|
|
Zн=1 Zк=2
|
Шаг 0.1 |
E=10-4 |
cos (z) |
|
|
|
Xн=0.1 Xк=1 |
Шаг 0.1 |
E=10-4 |
sin (x) |
|
|
|
Zн=1 Zк=2 |
Шаг 0.1 |
E=10-4 |
sin (z) |
|
|
|
Xн=0 Xк=2 |
Шаг 0.1 |
E=10-4 |
(1-2x2)ex^2 |
|
|
|
Xн=π/5 Xк= (9π)/5 |
Шаг π/5 |
E=10-3 |
-ln|2sin (x/2)| |
|
|
|
XН=0.1 XК=1 |
Шаг 0.1 |
E=10-4 |
ch x= (ex + e-x)/2 |
|
|
|
Xн=0.1 Xк=1 |
Шаг 0.1 |
E=10-4 |
sh x= (ex - e-x)/2 |
|
|
3x+ 8x2+….+n(n+2)xn |
Xн=0.1 Xк=0.8 |
Шаг 0.1 |
E=10-4 |
|
|
|
|
Xн = π/10 Xк = π/4
|
Шаг π/20 |
E=10-4 |
π2/8 – (π*|x|)/4 |
|
|
|
Xн=0.2 Xк=0.6 |
Шаг 0.05 |
E=10-4 |
arctg (x) |
|
|
|
Xн=0.1 Xк=0.8 |
Шаг 0.1 |
E=10-4 |
1/2 - (π/4)*|sin x| |
|
|
|
Xн=0 Xк=1 |
Шаг 0.1 |
E=10-4 |
e 2x |
|
|
|
Xн=0.1 Xк=1 |
Шаг 0.1 |
E=10-4 |
(x2/4+x/2+x) *e x/2 |
|
|
|
Xн=0.2 Xк=1 |
Шаг 0.1 |
E=10-4 |
|
|
|
|
Xн = π/5 Xк = π |
Шаг π/10 |
E=10-4 |
1/4*(x2-(π2/3)) |
|
|
|
Zн=0.1 Zк=0.5 |
Шаг 0.05 |
E=10-3 |
1-z*ln (2) |
|
|
|
Zн=0 Zк=1 |
Шаг 0.1 |
E=10-4 |
|
|
|
|
Xн=0.1 Xк=1 |
Шаг 0.1 |
E=10-4 |
|
|
|
|
Xн=0.5 Xк=2 |
Шаг 0.1 |
E=10-4 |
e-x |
|
|
|
Xн=0.1 Xк=1 |
Шаг 0.1 |
Е=10-4 |
(1+x2)/2* arctg (x) - x/2 |
|
|
|
Xн=0.1 Xк=0.8 |
Шаг 0.1 |
Е=10-3 |
|
|
|
1+3x2+…+ (2n+1) x2n/n! |
Xн=0.1 Xк=1 |
Шаг 0.1 |
E=10-4 |
|
|
|
|
Xн=0.2 Xк=1.2 |
Шаг 0.1 |
Е=10-4 |
|
|
|
-(x+(x2/2)+(x3/3)+…+(xn/n)…) |
Xн=0.1 Xк=1.1 |
Шаг 0.1 |
Е=10-4 |
|
|
|
-ln 2- cos 2x- cos (4x/2) – cos(2nx/n) |
Xн=0 Xк= π |
Шаг π/8 |
Е=10-3 |
ln |sin x| |
|
|
|
Xн=0.2 Xк=2 |
Шаг 0.2 |
E=10-4 |
ax |
|
|
|
Xн = -π Xк = π |
Шаг π/4 |
E=10-4 |
x |
Задание.
Вычислить сумму ряда с точностью ε для всех значений аргумента x, меняющегося от x начального до x конечного с шагом ∆x. Вычислить точное значение функции для каждого x, подсчитать ошибку вычислений по формуле
t= ((|сумма ряда – точное значение|)/точное значение)*100%
и количество шагов для достижения заданной точности.
Результат выполнения программ должен быть представлен в следующем виде:
|
Значение x |
Сумма ряда S |
Точное значение y |
Относительная ошибка в % t |
Количество шагов n |
|
|
|
|
|
|
|
|
|
|
|
|