
Итерационные методы решения систем линейных
.docИтерационные методы решения систем линейных
алгебраических уравнений
Метод простых итераций
Альтернативой
точным методам решения систем линейных
алгебраических уравнений являются
итерационные методы, основанные на
многократном уточнении
![]() – приближенно заданного решения системы
– приближенно заданного решения системы
![]() .
Верхним индексом в скобках здесь и далее
по тексту обозначается номер итерации
(совокупности повторяющихся действий).
.
Верхним индексом в скобках здесь и далее
по тексту обозначается номер итерации
(совокупности повторяющихся действий).
Суть простейшего итерационного метода – метода простых итераций, состоит в выполнении следующих процедур.
1. Исходная система
![]() преобразуется к равносильному виду:
преобразуется к равносильному виду:
![]() ,
(2.1)
,
(2.1)
где
![]() – квадратная матрица,
– квадратная матрица,
![]() – вектор,
– вектор,
![]() .
Это преобразование может быть выполнено
различными путями, но для обеспечения
сходимости итераций нужно добиться,
чтобы норма матрицы
.
Это преобразование может быть выполнено
различными путями, но для обеспечения
сходимости итераций нужно добиться,
чтобы норма матрицы
![]() была меньше единицы, то есть
была меньше единицы, то есть
![]() ,
где
,
где
 или
или
 .
.
2. Вектор
![]() принимается в качестве начального
приближения
принимается в качестве начального
приближения
![]() и далее многократно выполняются действия
по уточнению решения согласно рекуррентному
соотношению
и далее многократно выполняются действия
по уточнению решения согласно рекуррентному
соотношению
![]() ,
,
![]() (2.2)
(2.2)
или в развернутом виде

3. Итерации прерываются при выполнении условия
 ,
(2.3)
,
(2.3)
где
![]() – заданная точность, которую необходимо
достигнуть при решении задачи, или более
простого условия
– заданная точность, которую необходимо
достигнуть при решении задачи, или более
простого условия
![]() .
(2.4)
.
(2.4)
Замечания.
1) Процесс (2.2)
называется параллельным
итерированием,
так как для вычисления
![]() -го
приближения всех неизвестных учитываются
вычисленные ранее их
-го
приближения всех неизвестных учитываются
вычисленные ранее их
![]() -е
приближения.
-е
приближения.
2) Начальное
приближение
![]() может выбираться произвольно или из
некоторых соображений. При этом может
использоваться априорная информация
о решении или просто «грубая» прикидка.
может выбираться произвольно или из
некоторых соображений. При этом может
использоваться априорная информация
о решении или просто «грубая» прикидка.
Теорема 2.1.
(достаточное
условие сходимости метода простых
итераций). Метод простых итераций,
реализующийся в процессе последовательных
приближений (2.2), сходится к единственному
решению исходной системы
![]() при любом
начальном приближении
при любом
начальном приближении
![]() со скоростью не медленнее геометрической
прогрессии, если норма матрицы
со скоростью не медленнее геометрической
прогрессии, если норма матрицы
![]() меньше единицы, то есть
меньше единицы, то есть
![]() .
.
Замечания.
1) Условие теоремы
2.1, как достаточное, предъявляет завышенные
требования к матрице
![]() ,
и поэтому иногда сходимость будет, если
даже
,
и поэтому иногда сходимость будет, если
даже
![]() .
.
2) Сходящийся процесс обладает свойством самоисправляемости, то есть отдельная ошибка в вычислениях не отразится на окончательном результате, так как ошибочное приближение можно рассматривать как новое начальное.
3) Условия сходимости
выполняются, если в матрице
![]() преобладают диагональные элементы, то
есть
преобладают диагональные элементы, то
есть
![]() ,
,
![]() ,
(2.5)
,
(2.5)
и хотя бы для одного
![]() неравенство строгое. Иначе, модули
диагональных коэффициентов в каждом
уравнении системы больше суммы модулей
недиагональных коэффициентов (свободные
члены не рассматриваются).
неравенство строгое. Иначе, модули
диагональных коэффициентов в каждом
уравнении системы больше суммы модулей
недиагональных коэффициентов (свободные
члены не рассматриваются).
4) Чем меньше
величина нормы
![]() ,
тем быстрее сходимость метода.
,
тем быстрее сходимость метода.
5) Из неравенства
(2.3) еще до начала расчета можно получить
число итераций
![]() ,
требуемых для достижения заданной
точности:
,
требуемых для достижения заданной
точности:
 ,
(2.6)
,
(2.6)
где норма вектора
![]() определяется следующим образом:
определяется следующим образом:
![]() или
или
 .
.
Преобразование
системы
![]() к виду
к виду
![]() с матрицей
с матрицей
![]() ,
удовлетворяющей условиям сходимости,
может быть выполнено несколькими
способами. Приведем способы, используемые
наиболее часто.
,
удовлетворяющей условиям сходимости,
может быть выполнено несколькими
способами. Приведем способы, используемые
наиболее часто.
1. Уравнения,
входящие в систему
![]() ,
переставляются так, чтобы выполнялось
условие (2.5) преобладания диагональных
элементов. Затем первое уравнение
разрешается относительно
,
переставляются так, чтобы выполнялось
условие (2.5) преобладания диагональных
элементов. Затем первое уравнение
разрешается относительно
![]() ,
второе – относительно
,
второе – относительно
![]() и т.д. При этом получается матрица
и т.д. При этом получается матрица
![]() с нулевыми диагональными элементами.
с нулевыми диагональными элементами.
Пример 1. Система

с помощью перестановки уравнений приводится к виду

где
![]() ,
,
![]() ,
,
![]() ,
то есть диагональные элементы преобладают.
,
то есть диагональные элементы преобладают.
Выражая
![]() из первого уравнения,
из первого уравнения,
![]() – из второго,
– из второго,
![]() – из третьего, получим систему
– из третьего, получим систему

где
 ,
,
 .
.
Заметим, что
![]() ,
то есть условие теоремы 2.1. выполнено.
,
то есть условие теоремы 2.1. выполнено.
2. Уравнения
преобразуются так, чтобы выполнялось
условие преобладания диагональных
элементов, но при этом коэффициенты
![]() не обязательно равнялись нулю.
не обязательно равнялись нулю.
Пример 2. Систему

можно записать в форме

для которой
![]() .
.
Пример 3.
Методом простых итераций с точностью
![]() решить систему линейных алгебраических
уравнений
решить систему линейных алгебраических
уравнений

Предварительно определить число итераций.
Решение.
Так как
![]() ,
,
![]() ,
,
![]() ,
условие (2.5) не выполняется. Переставим
уравнения местами так, чтобы выполнялось
условие преобладания диагональных
элементов:
,
условие (2.5) не выполняется. Переставим
уравнения местами так, чтобы выполнялось
условие преобладания диагональных
элементов:

Получим
![]() ,
,
![]() ,
,
![]() .
Выразим из первого уравнения
.
Выразим из первого уравнения
![]() ,
из второго
,
из второго
![]() ,
из третьего
,
из третьего
![]() :
:

 ,
,
 .
.
Заметим, что
![]() ,
,
![]() ,
,
следовательно, условие сходимости выполнено.
По формуле (2.6) вычислим число итераций, обеспечивающих заданную точность:
 ;
;
![]() .
.
Таким образом, для решения задачи необходимо выполнить не менее пяти итераций.
Зададим
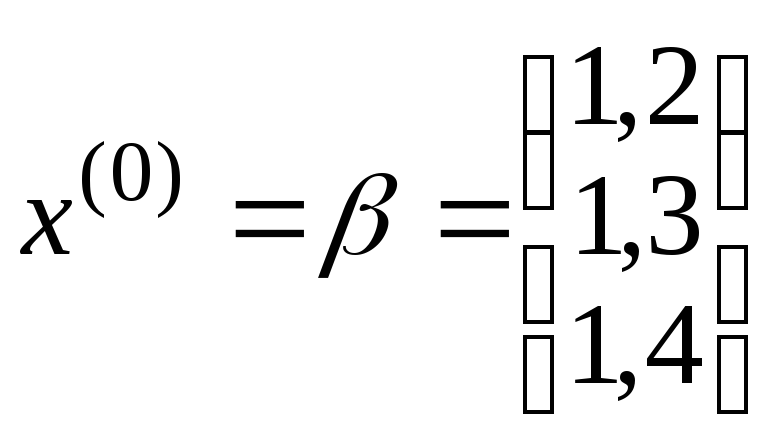 .
В поставленной задаче
.
В поставленной задаче
![]() .
.
Выполним расчеты по формуле (2.2):
 ,
,
![]() ,
,
или

![]()
Результаты вычислений оформим в виде таблицы 2.1.
Таблица 2.1
|
|
|
|
|
|
|
0 |
1,2000 |
1,3000 |
1,4000 |
- |
|
1 |
0,9300 |
0,9200 |
0,9000 |
0,5 |
|
2 |
1,0180 |
1,0240 |
1,0300 |
0,13 |
|
3 |
0,9946 |
0,9934 |
0,9916 |
0,0384 |
|
4 |
1,0015 |
1,0020 |
1,0024 |
0,0108 |
|
5 |
0,9996 |
0,9995 |
0,9993 |
0,0027< |
Таким образом, приближенное решение задачи:
![]() .
.
Очевидно, точное
решение:
![]() .
.
