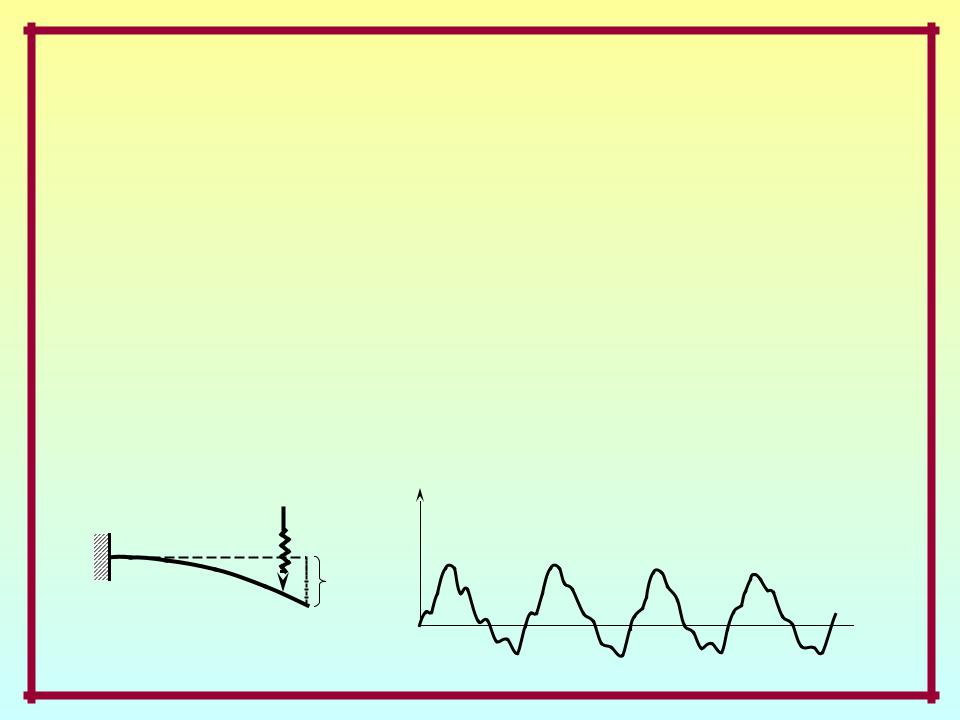
Колебания (механические) –
частный случай движения, характеризующийся некоторой повторяемостью во времени параметров НДС системы.
F(t) y(t)
y(t)
0 
t
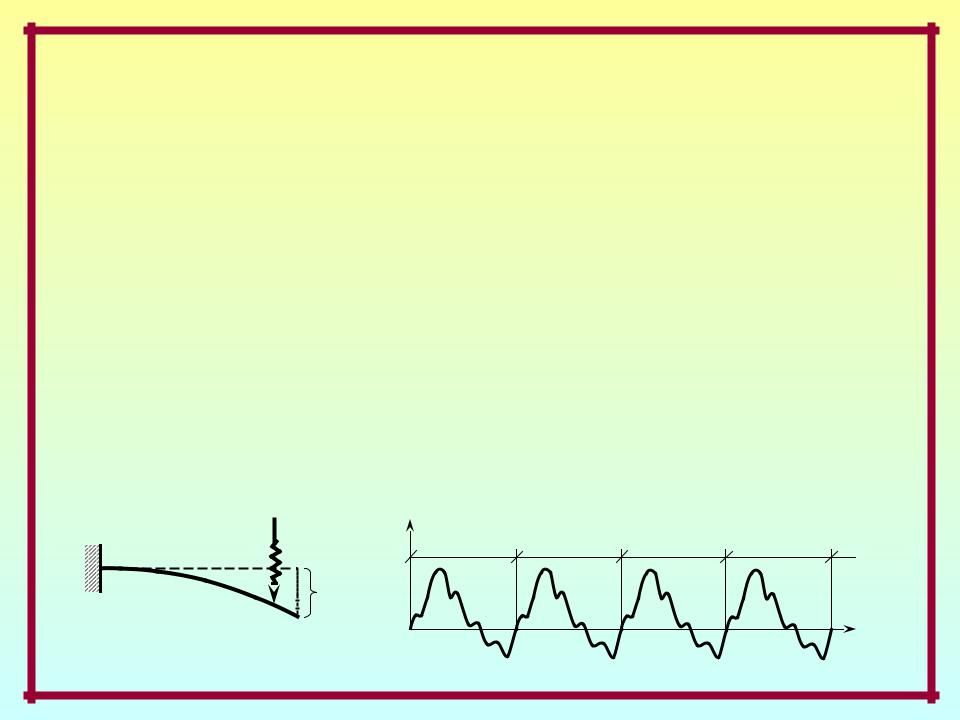
Периодические колебания –
колебания, при которых значения некоторого (любого) параметра Р(t)
НДС системы в точности повторяются
через один и тот же промежуток времени Т, называемый периодом колебаний:
P(t) = P(t +kT ), где k – любое целое число.
F(t) |
y(t) |
Т |
Т |
Т |
|
Т |
|||
|
y(t) |
|
|
|
|
0 |
|
|
t |
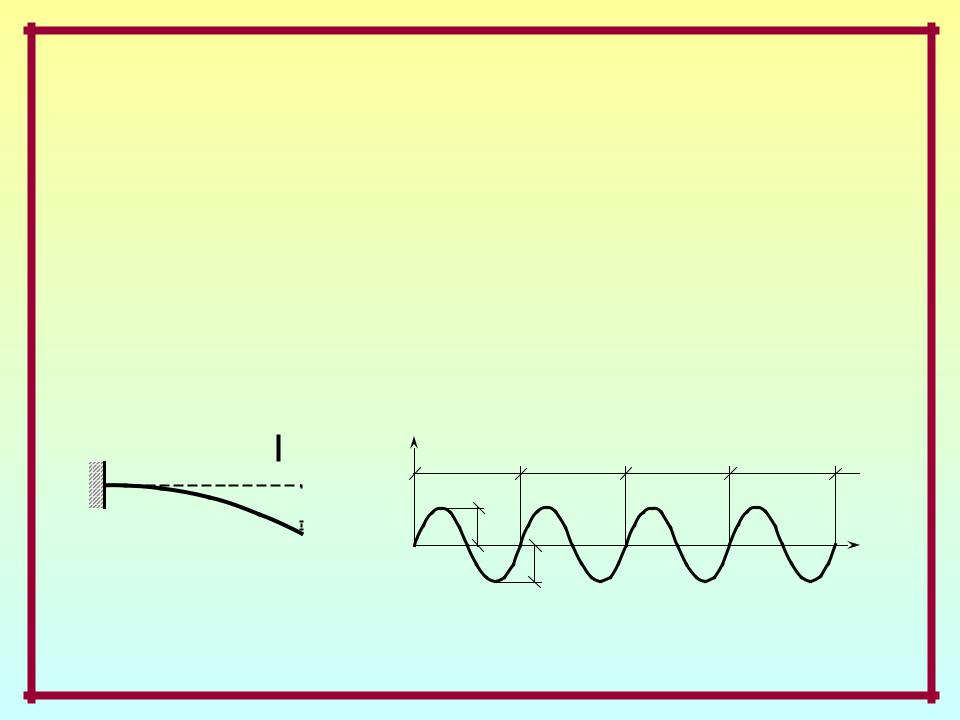
Гармонические колебания –
колебания, при которых динамические составляющие параметров НДС системы изменяются во времени
по гармоническому закону
(синуса или косинуса).
F(t)
y(t)
y(t) y sin(ωF t 0 )
(cos)
F – угловая частота
гармонического
воздействия
y(t) |
Т |
Т |
Т |
Т |
|||
0 |
y |
|
t |
y |
|
||
|
|
|
|
y – амплитуда перемещения |
|||
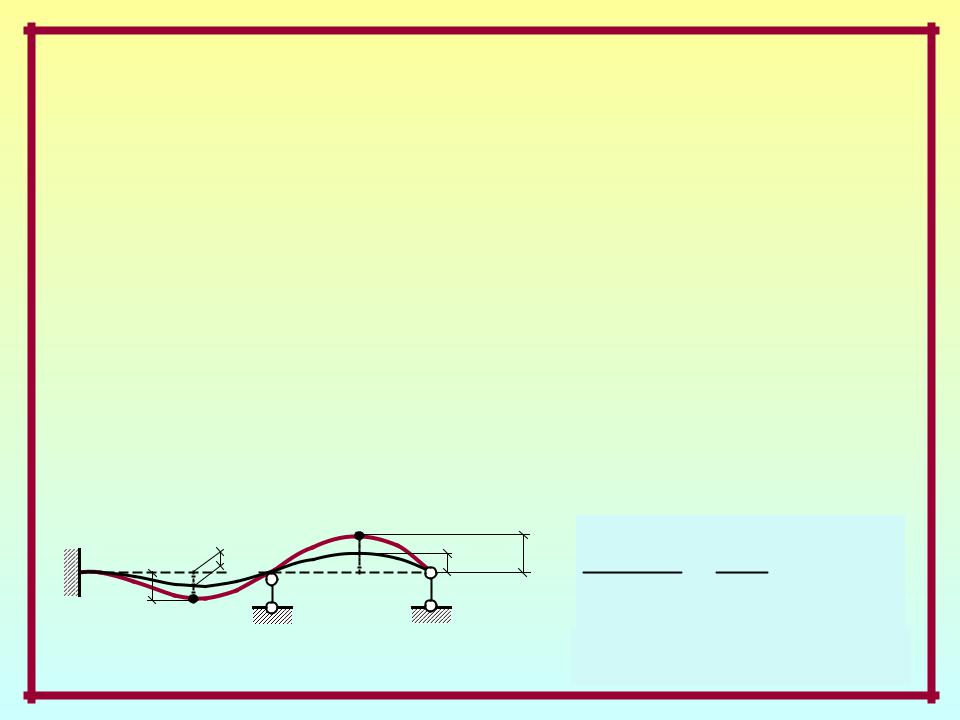
Собственные колебания –
частный случай свободного движения, характеризующийся
синфазным моногармоническим
движением всех масс системы (то есть гармоническим движением масс
с одной общей частотой и в одной фазе (t)): yi (t) = yi sin (t), i = 1, 2, ... , n; (t) = t + 0.
– угловая частота собственных колебаний |
|||||||
|
y |
(t) |
k |
y |
|
yi (t) |
yi |
|
yk(t) |
|
|||||
yi |
i |
|
|
k |
yk (t) |
yk const |
|
|
i |
|
|
|
|
(стоячая волна) |
|
|
|
|
|
|
|
||
Главная форма колебаний –
определенный вид стоячих волн, образуемых осевыми линиями или срединными поверхностями элементов системы
при собственных колебаниях с некоторой частотой.
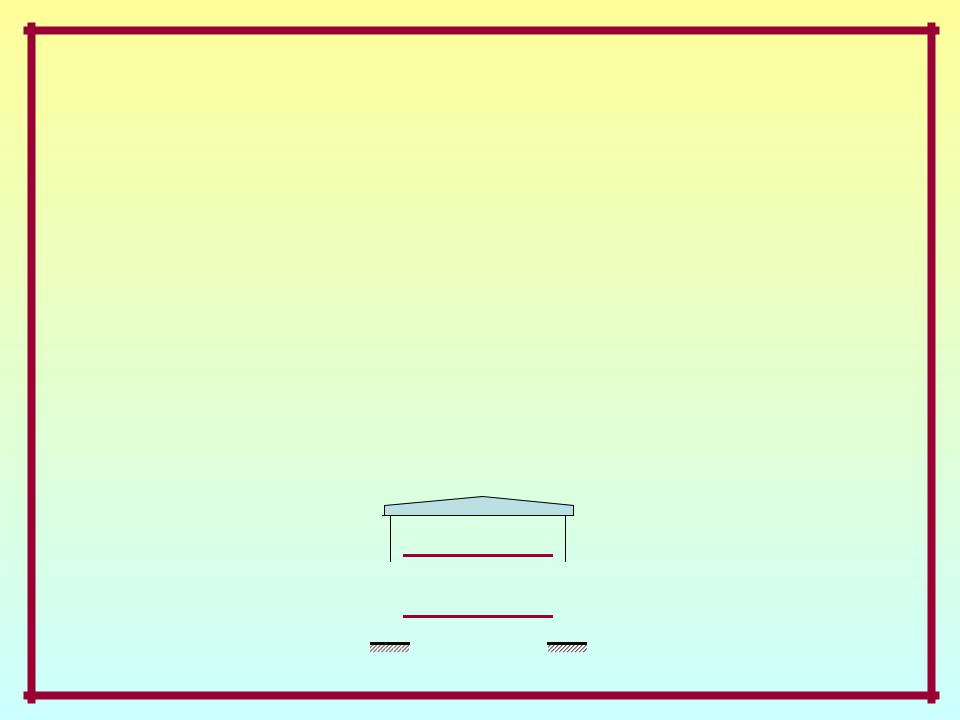
Степени свободы масс –
независимые геометрические параметры, полностью определяющие положение масс системы в произвольный момент движения.
Системы с распределёнными массами
n 
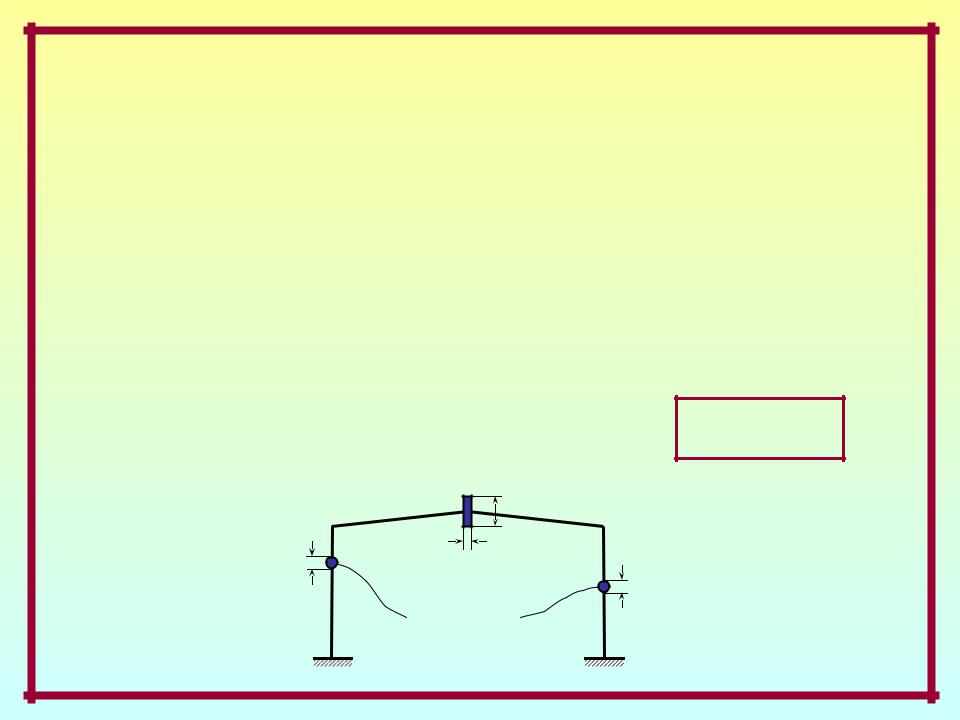
Степени свободы масс –
независимые геометрические параметры, полностью определяющие положение масс системы в произвольный момент движения.
Системы с сосредоточенными массами:
Неточечная |
h |
|
||
масса |
|
|
||
ds |
ds |
|
ds |
|
Точечные |
||||
|
||||
массы |
|
|
||
1 n
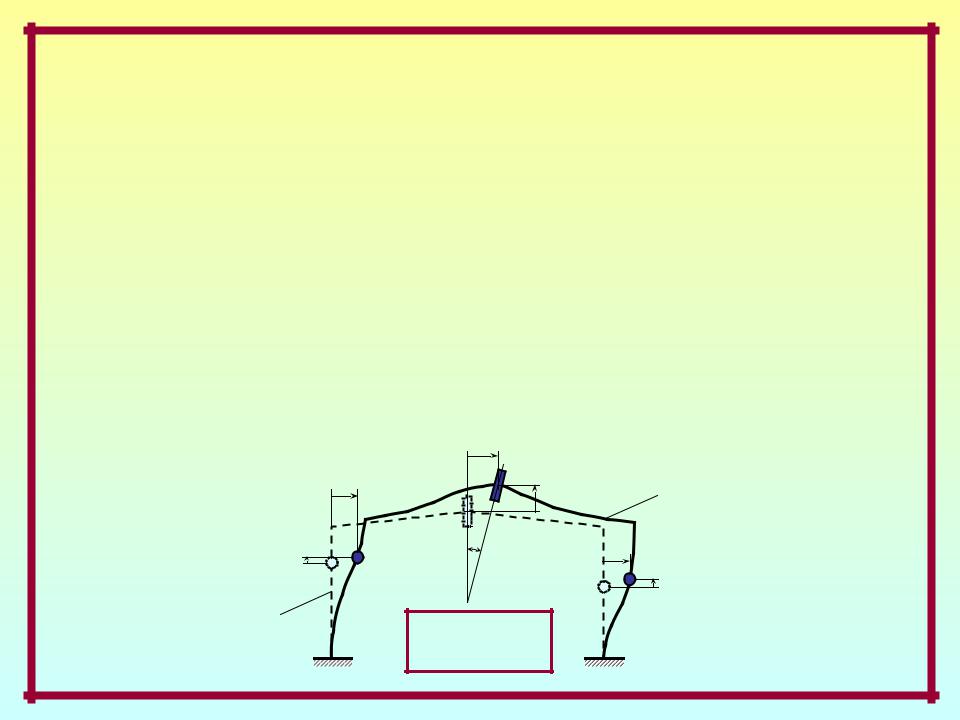
Степени свободы масс –
независимые геометрические параметры, полностью определяющие положение масс системы в произвольный момент движения.
y1(t) |
y3(t) |
|
|
y4(t) |
В момент |
||
|
|
времени t |
|
y2(t) |
y5(t) |
y6(t) |
|
y7(t) |
|||
До начала |
n = 7 |
||
движения |
|
||
|
|
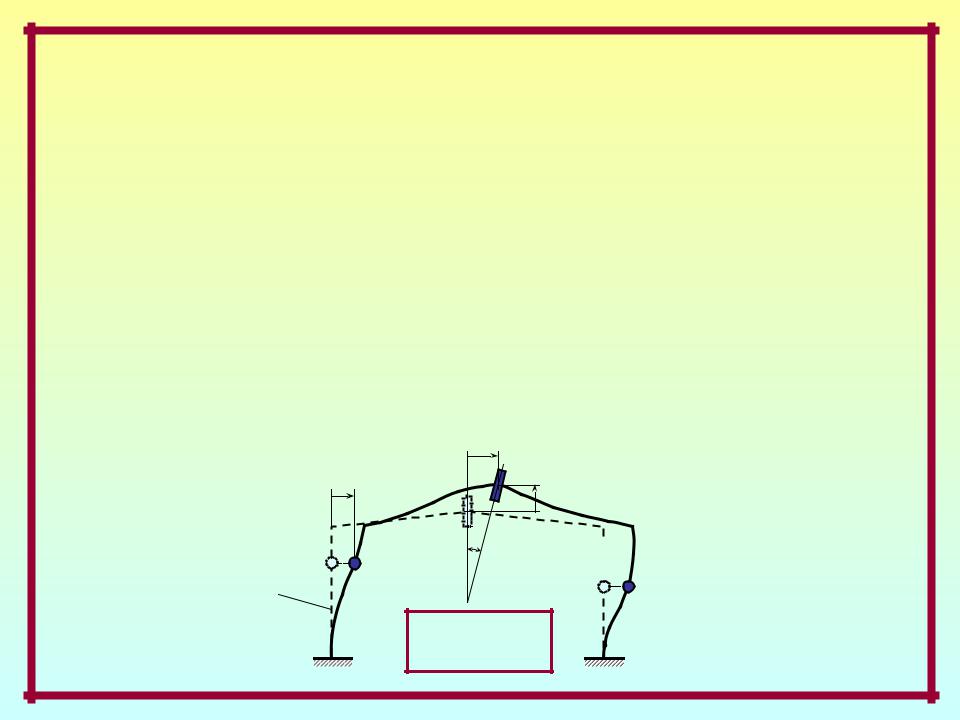
Степени свободы масс –
независимые геометрические параметры, полностью определяющие положение масс системы в произвольный момент движения.
В случае применения |
|
y2(t) |
гипотезы l j l j : |
y1(t) |
y3(t) |
|
||
До начала |
|
y4(t) |
движения |
|
n = 5 |
|
|
В момент 
времени t
y5(t)
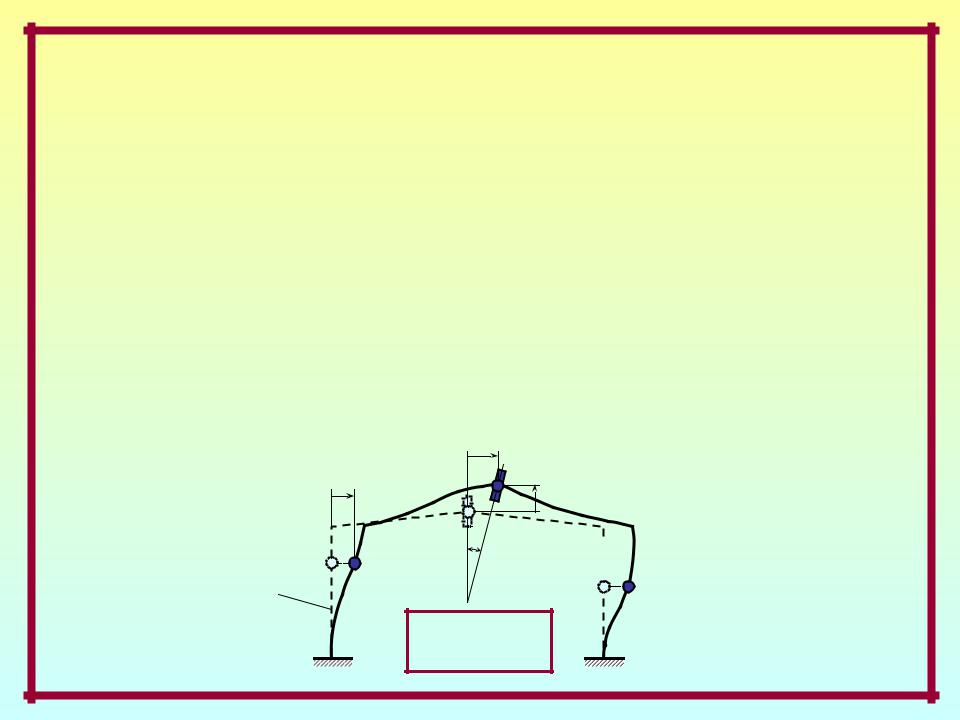
Степени свободы масс –
независимые геометрические параметры, полностью определяющие положение масс системы в произвольный момент движения.
В случае применения |
|
|||
гипотезы |
l j |
l j |
: |
|
|
|
y1(t) |
||
Если не учитывать |
||||
инерцию поворота |
|
|||
средней |
|
|
||
массы: До начала |
|
|||
движения |
|
|||
y2(t) |
y3(t) |
y4(t) |
n = 54 |
В момент 
времени t
y54(t)