Строительная механика.
Часть III
ДИНАМИКА
СООРУЖЕНИЙ
ДИНАМИКА СИСТЕМ
С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ МАСС
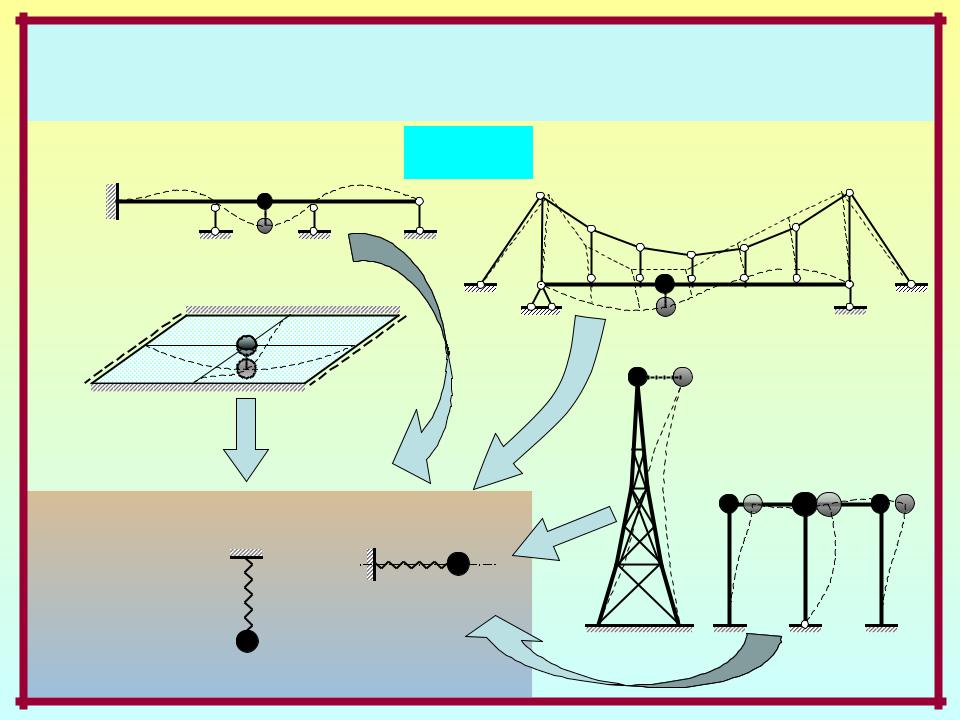
Динамика систем с одной степенью свободы масс
n = 1
Обобщённая расчётная модель |
|
|
c |
c |
m |
m
Динамика систем с одной степенью свободы масс
Предпосылки и рабочие гипотезы
линейной теории динамических расчётов систем с конечным числом степеней свободы масс
(в том числе с n = 1)
1.Рассматриваются линейно деформируемые системы.
2.Массы сосредоточенные, элементы системы невесомые.
3.Сопротивление внешней среды и внутреннее трение в системе
учитываются по модели вязкого трения.
4. Исследуется движение системы относительно её исходного состояния, в качестве которого принимается
состояние равновесия, вызванное статическими воздействиями
(постоянными и временными нединамическими ).
5.Определению подлежат динамические составляющие
напряжённо-деформированного состояния движущейся системы (перемещения, усилия, напряжения, деформации ).
Динамика систем с одной степенью свободы масс
Определение характеристики жёсткости обобщённой расчётной модели линейно деформируемой системы с одной степенью свободы масс
F = 1 |
|
|
F = 1 |
||
|
|
|
|
||
11 |
|
|
|
|
11 |
F = 1 |
|
|
|
11 |
|
|
|
F = 1 |
11 – упругая |
||
|
|
|
|||
|
11 |
|
|
податливость системы |
|
|
|
|
|
||
|
|
|
|
в точке расположения |
|
|
|
|
|
|
массы по направлению |
Обобщённая расчётнаяcмодель |
|
|
F = 1 её11 движения |
||
|
|
|
|||
c |
c 1 |
m |
|
|
|
|
|
|
|
|
|
m |
δ11 |
|
|
|
m = mj |
|
|
|
|
|
Динамика систем |
|
|||
с одной степенью свободы масс |
|||||||||
|
Обобщённая |
|
Математическа |
|
|||||
расчётная модель |
|
|
я |
|
|||||
|
( свободное |
|
модель |
|
|||||
|
движение ) |
1. Статическая сторона задачи |
|||||||
|
|
( уравнение равновесия ) |
|
||||||
статическогоПоложение |
|
c |
|
|
y = 0: |
|
|||
m 0 |
|
|
|
||||||
равновесия |
|
|
R(t) y(t) |
J(t) + FD (t) + R(t) = 0 ( 1 ) |
|||||
|
|
|
|
|
|||||
Вязкая |
m |
|
|
2. |
Геометрическая сторона задачи |
||||
|
R(t) – реакция |
( условие совместности |
|
||||||
среда |
|
|
|
|
|||||
|
|
FD (t) |
|
дискретной связи |
деформации дискретной связи |
||||
Сила |
|
|
и перемещения массы ) |
|
|||||
|
|
|
|
J(t) – сила инерции |
lc (t) = y(t) |
( 2 ) |
|||
сопротивле- |
|
y |
|
|
|||||
ния (реакция) |
|
|
|||||||
вязкой среды |
|
3. Физическая сторона задачи |
|
||||||
– закон Гука ( для дискретной упругой связи ): |
R(t) c lc (t) |
( 3 ) |
|||||||
– закон инерции ( для силы инерции Д’Аламбера ): |
J (t) m y(t) |
||||||||
– закон вязкого сопротивления ( по модели Фойгта ): |
FD (t) k f y(t) |
||||||||
|
|
|
|
|
|
|
W. Voigt |
kf – коэффициент сопротивления |
|
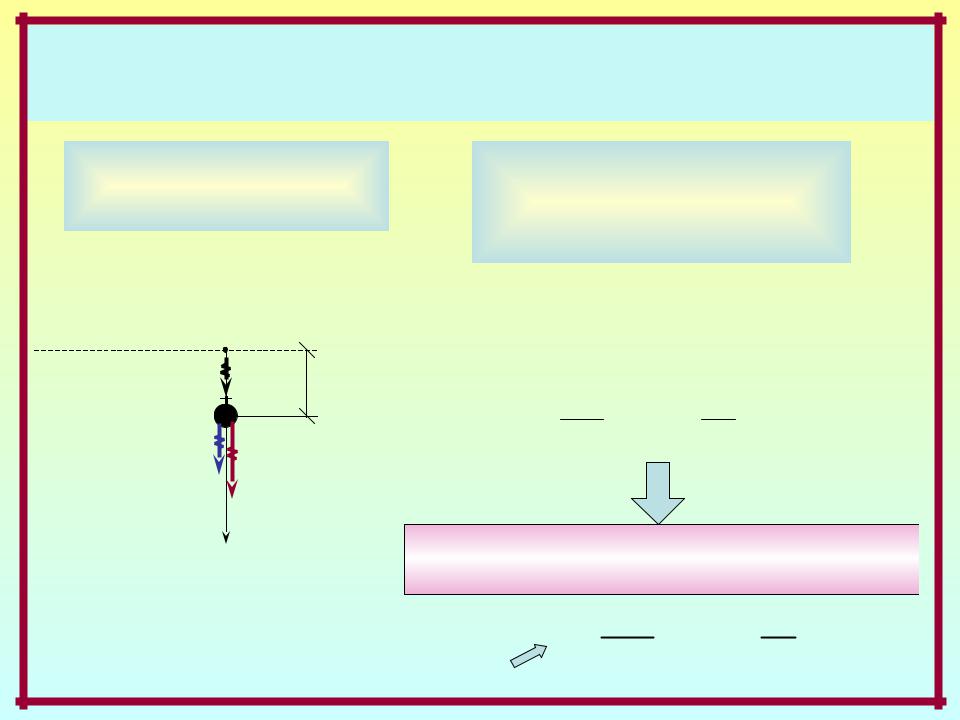
Динамика систем с одной степенью свободы масс
Обобщённая |
Математическа |
||||
расчётная модель |
|
я |
|
||
( свободное |
|
модель |
|||
движение ) |
Разрешающее уравнение – |
||||
дифференциальное уравнение |
|||||
Положение |
0 |
свободного движения: |
|||
m y(t) k f y(t) c y(t) 0 |
|||||
|
|||||
статического |
|
|
|
||
равновесия |
R(t) y(t) |
|
или |
c y(t) 0 |
|
|
y(t) |
||||
m |
|
k f y(t) |
|||
|
|
m |
m |
||
FD (t) |
J(t) |
|
|
|
|
|
y(t) 2β y(t) ω1 y(t) 0 |
||||
|
y |
|
|
2 |
|
Коэффициент демпфирования |
β k f ; |
ω12 c |
|||
2m |
m |
||||
Динамика систем с одной степенью свободы масс
Решение дифференциального уравнения свободного движения системы
с одной степенью свободы масс
y(t) 2β y(t) ω12 y(t) 0.
Характеристическое уравнение:
r β β2 |
ω2 |
β i ω , |
|
||||||||
1,2 |
|
1 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
c |
|
|
k f |
2 |
|
где ω ω2 |
β2 |
|
|||||||||
|
|
||||||||||
1 |
|
|
|
|
m |
|
|
||||
|
|
|
|
|
|
2m |
|||||
Уравнение свободного движения
при 2 < c /m:
y(t) = a0e – t sin ( t + 0 )
– угловая частота свободных колебаний системы с одной степенью свободы
Динамика систем с одной степенью свободы масс
Уравнение свободного движения при 2 < c /m:
y(t) = a0e – t sin ( t + 0 ),
|
|
|
|
|
βv0 |
|
2 |
|
|
y0 |
|
|
a0 |
y0 |
; |
0 |
arcsin |
||||
|
где |
y02 |
|
ω |
|
a0 |
||||
|
|
|
|
|
|
|
|
|||
y(t) a0e – t |
начальная амплитуда |
|
|
начальная фаза |
||||||
T |
|
|
|
|
|
|
|
|||
|
|
|
ln ai |
T – логарифмический |
||||||
а0 y0 |
|
аi |
|
|
ai 1 |
|
|
|
декремент |
|
|
|
ai +1 |
|
|
|
затухания |
||||
T |
0 |
|
|
|
|
|
|
|
|
t |
0 2π |
|
|
|
– a0e |
|
|
|
|||
а0 |
T |
|
T |
|
– t |
|
|
|||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||
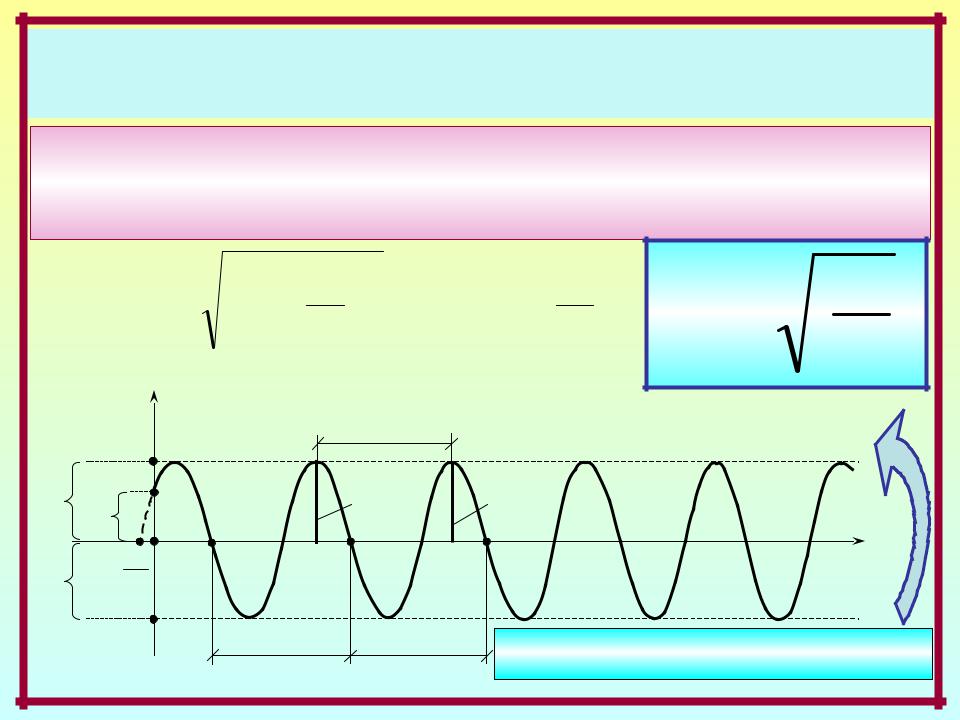
Динамика систем с одной степенью свободы масс
Уравнение свободного движения при = 0 ( kf = 0 ):
y(t) = a0 sin ( t + 0 )
|
|
|
|
a0 |
|
y0 |
|
2 |
; |
0 arcsin |
y0 |
; |
ω |
c |
|
|
|
где |
y02 |
ω |
|
|
a0 |
||||||||
|
|
|
|
|
|
|
|
|
|
m |
|||||
|
|
|
y(t) |
Логарифмический |
|
|
|
|
|||||||
|
|
|
|
|
декремент затухания = 0 |
– частота (угловая) |
|||||||||
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
собственных |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
колебаний |
|
а |
0 |
y0 |
|
|
|
|
а |
i |
|
ai +1 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|||
а0 |
|
T |
|
|
|
|
|
|
|
|
|
|
|
||
0 2π |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
T |
|
|
|
|
T |
СОБСТВЕННЫЕ КОЛЕБАНИЯ |
||||
|
|
|
|
|
|
|
|
|
|
|
|||||
Динамика систем с одной степенью свободы масс
Обобщённая |
|
Математическа |
|||
расчётная модель |
|
я |
|||
( вынужденное |
|
модель |
|||
движение ) |
|
Статическая сторона задачи |
|||
|
( уравнение равновесия ) |
||||
|
|
c |
|
|
y = 0: |
статическогоПоложение |
|
|
J(t) + FD (t) + R(t) + F(t) = 0 |
||
m |
0 |
|
|||
равновесия |
|
R(t) y(t) |
|
|
|
|
|
Дифференциальное уравнение |
|||
Вязкая |
m |
J(t) |
|
||
среда |
|
|
вынужденного движения |
||
FD (t) |
F(t) |
y(t) 2β y(t) ω2 y(t) F(t)/m |
|||
|
|
||||
|
|
y |
|
β k f |
1 |
|
|
|
; ω12 c |
||
|
|
|
|
2m |
m |