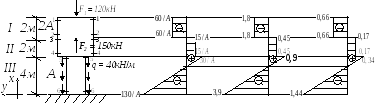
2. Построение эпюры напряжений

Зная, что при центральном сжатии (растяжении) σ=σ_x=N_x/A и учитывая заданное соотношение между площадями на грузовых участках (I, II - 2А, III - А), построим эпюру напряжений через отношения N_x/A. Это эпюра строится с целью нахождения опасных сечений. Выполним необходимые вычисления.

Эп. N[кН] Эп. σ

σ_1-1=σ_2-2=N_1-1/2А=-120/2А=-60/А;

σ_3-3=σ_4-4= N_3-3/2А =30/2А=15/А;

σ_5-5= N_5-5/А =30/А;

σ_6-6= N_6-6/А =-130/А;

С помощью эпюры напряжений (σ=N/A) найдем опасные сечения. В настоящей задаче будет два опасных сечения (σ_max и σ_min), т.к. во-первых, материал хрупкий (R_t≠R_c), а во-вторых, эпюра напряжений имеет два знака, следовательно, материал необходимо рассчитать для работы и на сжатие и на растяжение. Если материал пластичный (R_t=R_c), то будет одно опасное сечение (/σ/_max). Также одно опасное сечение для хрупкого материала будет в том случае, когда эпюра напряжений имеет один знак («+» σ_max или «-» σ_min).

Опасное сечение в растянутой зоне σ_max=σ_5-5=30/А;

Опасное сечение в сжатой зоне σ_min=σ_6-6=-130/А.

3. Определение площади поперечного сечения

С целью нахождения площади поперечного сечения запишем условия прочности.

Условие прочности на растяжение

Условие прочности на сжатие

Сравним две найденные площади и примем к последующему расчету наибольшую, найденную из условия прочности на растяжение А=0,0333м².

Зная площадь поперечного сечения можно получить числовые значения напряжений и выставить их на эпюру.

4. Построение эпюры деформаций

По закону Гука σ=Еε, тогда ε=σ/Е. Определим значения деформаций в сечениях с помощью эпюры напряжений.

ε_1-1= ε_2-2=σ_1-1/Е=-1,8/(2,7·10⁴)=-0,66·10^-4;

Ε_3-3=ε_4-4=σ_3-3/Е=0,45/(2,7·10⁴)=0,17·10^-4;

ε_5-5=σ_5-5/Е=0,9/(2,7·10⁴)=0,34·10^-4;

ε_6-6=σ_6-6/Е=-3,9/(2,7·10⁴)=-1,44·10^-4.

Опираясь на выполненные расчеты, построим эпюру деформаций.

Эп. σ Эп. σ[МПа] Эп. ε×10⁴

5. Построение эпюры перемещений

Перемещения представляют собой сумму интегралов от функции внутреннего усилия, отнесенного к жесткости стержня. Интегрирование ведется в пределах грузового участка.

При построении эпюры перемещений u необходимо строго следить за выполнением дифференциальных зависимостей:

Геометрическим смыслом первой производной функции является тангенс угла наклона касательной к графику функции. В случае, когда первая производная обращается в ноль, функция имеет экстремум.

Геометрическим смыслом интеграла является площадь, ограниченная графиком функции.

Для получения перемещений можно интегрировать функцию продольных сил, функцию напряжений или функцию деформаций. В данном случае рациональнее всего работать с функцией деформаций. Помня о геометрическом смысле интеграла можно найти значения перемещений, суммируя площади эпюры деформаций. Определение перемещений всегда начинают с того сечения, в котором известно перемещение, в нашем случае – это заделка (u_6-6=0). В пределах грузовых участков, где деформация (напряжение, продольное усилие) постоянна, перемещение определяют как .

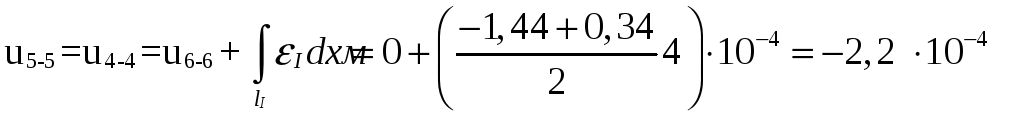, затем определим перемещения при x=3,25м ;

;

.

Найдя значения перемещений во всех сечениях (параболу строят по трем точкам) приступают к построению эпюры перемещений.

Эп. N[кН] Эп. σ[МПа] Эп. ε×10⁴ Эп. u[10^-4м]

6. Учет собственного веса колонны при построении эпюр Эп. N[кН]

Определим вес колонны на грузовых участках:

I грузовой участок Р_I=р·2Аx₁=25 2 0,03x₁=1,6x₁,

при x₁=0 Р_I=0, при x₁=2м Р_I=3,3кН;

II грузовой участок Р_II=р 2Аx₂=25 2 0,03x₂=1,6;

при x₂=0 Р_II=0, при x₂=2м Р_II=3,3кН;

III грузовой участок Р_III=р Аx₃=25 0,03x₃=0,825x₃;

при x₃ =0 Р_III=0 при x₃=4м Р_III=3,3кН.

Вес всей колонны составляет Р_I+Р_II+Р_III=3,3+3,3+3,3=9,9кН.

Эпюра продольных сил только от собственного веса колонны приведена справа.

Эп. N(Р)[кН] Эп. σ(Р)[МПа] Эп. u(Р)[10^-4м]

Построим эпюру продольных сил с учетом собственного веса:

N_I=-F₁-р 2Аx₁, тогда N_1-1=-120кН, N_2-2=-120-Р_I=-120-3,3=-123,3кН

N_II=-F₁-Р_I+F₂-р 2Аx₂=-120-3,3+150-р 2Аx₂, тогда

N_3-3=-123,3+150=26,7кН, N_4-4=26,7-3,3=23,4кН

N_III=-F₁- Р_I+F₂-Р_II-qx-р Аx₃=-120-3,3+150-3,3-40x₃-р Аx₃,

тогда N_5-5=23,4кН, N_6-6=23,4-40 4-3,3 =-139,9кН. В пределах третьего грузового участка внутреннее усилие меняет знак, найдем расстояние от заделки до сечения, в котором N=0: N_III=-139,9+40x₃+25 0,03x₃=0 => x₃=139,9/4075=3,4м (при этом значении x функция перемещений u имеет экстремум).

Построим эпюру напряжений с учетом собственного веса:

σ_1-1= N_1-1/2А=(-120 10^-3)/(2 0,033)=-1,8МПа;

σ_2-2=N_2-2/2А=(-123,3 10^-3)/(2 0,033)=-1,85МПа;

σ_3-3= N_3-3/2А=(26,7 10^-3)/(2 0,033)=0,4МПа;

σ_4-4= N_4-4/2А=(23,4 10^-3)/(2 0,033)=0,35МПа;

σ_5-5= N_5-5/А=(23,4 10^-3)/0,033=0,7МПа;

σ_6-6= N_6-6/А =(-139,9 10^-3)/0,033=-4,2МПа.

Построим эпюру перемещений с учетом собственного веса:

Рассмотрим два способа.

Первый способ. Получим перемещения путем интегрирования функции продольной силы. .

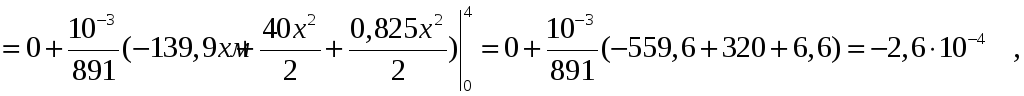
затем определим перемещения при x=3,4м

.

Далее перемещения получают аналогично.

Второй способ. Расчет произведем с помощью эпюры напряжений, помня о том, что геометрический смысл интеграла - это площадь, а перемещение на грузовом участке можно представить в виде .

, затем определим перемещения при x=3,4м ;

;

.

По данным строят эпюру перемещений.

20