Расчёт на прочность и жёсткость при осевом растяжении (сжатии)

Осевое или центральное растяжение (сжатие) относят к простым видам сопротивления. Название этого вида деформации обусловлено тем, что линия действия сил, приложенных к стержню, совпадает с осью стержня (ось стержня проходит через центры тяжести поперечных сечений). При осевом растяжении (сжатии) в силу принятых гипотез σ_y=σ_z=τ_yx=τ_yz=0, σ_x≠0, поэтому напряженное состояние в элементе объёма – линейное (только одно из главных напряжений отлично от нуля). Нормальное напряжение в поперечном сечении при данном виде деформации является функцией от продольного внутреннего усилия N_x и зависит от геометрической характеристики поперечного сечения – площади А. Определяют напряжение по формуле σ=σ_x=N_x/A.

При растяжении (сжатии) различают абсолютные ∆l и относительные ε деформации. Абсолютная деформация – это разница между длиной стержня до и после деформации, т.е. та величина, на которую он изменил свою длину ∆l=/l₁-l/. Относительная деформация – это, как ясно из названия, отношение абсолютной деформации к первоначальной длине стержня ε=∆l/l.

Для расчета на прочность пользуются условием прочности, которое при данном виде сопротивления имеет вид:

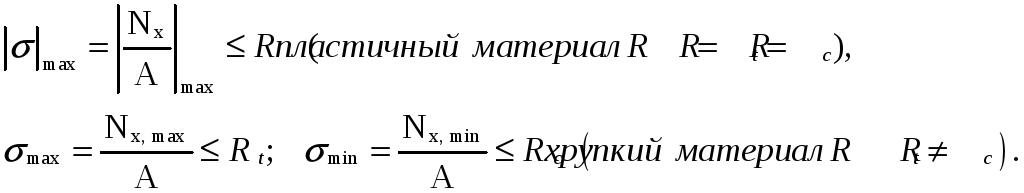
В этих выражениях , , - расчетные сопротивления по нормальным напряжениям для хрупкого и пластичного материала соответственно. Максимальное значение напряжения определяют с помощью эпюры напряжений, полученной через отношения N_x/A.

В расчете на жесткость применяют условия жесткости: .

Первое условие для полного перемещения стержня, а второе - для максимального перемещения сечения. В квадратных скобках приведены допустимые значения. Для определения опасного сечения, в котором возникает, строят эпюру перемещений. Ниже приведен пример выполнения статически определимой задачи, входящей в состав индивидуального задания № 2.

Задача 2. Расчет на прочность и жесткость при осевом растяжении (сжатии). Построение эпюр продольных сил, напряжений, деформаций и перемещений

Дано: F₁=120кН, F₂=150кН, q=40кН/м, Е=0,27×10⁵МПа,

удельный вес р=25кН/м³; материал хрупкий, поэтому

расчетное сопротивление растяжению ,

расчетное сопротивление сжатию

Требуется: определить площадь поперечного сечения

из условия прочности (соотношение площадей задано),

построить эпюры продольной силы, напряжений,

деформаций и перемещений с учетом собственного веса и без него.

Эп. N[кН] Эп. σ Эп. σ[МПа] Эп. ε×10⁴ Эп. u[10^-4м]

Решение

1. Построение эпюры внутренних усилий (продольной силы)

Эпюрой внутреннего усилия называют график функции, описывающей внутреннее усилие. Под действием внешних нагрузок (сосредоточенные и равномерно распределенные нагрузки), приложенных таким образом, что стержень подвергается центральному растяжению (сжатию), в нем возникает внутренние усилия – продольные силы. Для построения эпюры необходимо на всех грузовых участках составить уравнения внутренних усилий. Используем метод сечений. Суть метода заключается в следующем. Рассматриваемый элемент мысленно рассекают на две части (проводят сечение), одну часть отбрасывают (целесообразно отбрасывать ту часть, на которую действует больше нагрузок), а действие отброшенной части заменяют положительно направленными внутренними усилиями (в данном случае N). Любой элемент должен находиться в равновесии, поэтому составляют уравнения статики (уравнения равновесия) из которых находят значения внутренних усилий. Правило знаков для продольного внутреннего усилия следующее: внутреннее усилие (N) будет положительным при растяжении элемента и отрицательным в случае сжатия.

Продольное внутреннее усилие (N) в любом сечении равно алгебраической сумме проекций всех внешних сил (включая опорные реакции), взятых по одну сторону от сечения, на продольную ось стержня.

Расчет начнем с верхней части, нижнюю часть мысленно отбросим. Рассмотрим первый и второй грузовые участки.

Рассмотрим первый грузовой участок: N_I=-F₁=-120кН – const, т.е. N_1-1= N_2-2=-120кН

Рассмотрим второй грузовой участок: N_II=-F₁+ F₂=-120+150=30кН – const,

т.е. N_3-3=N_4-4=30кН

Рассмотрим третий грузовой участок: N_III=-F₁+ F₂-qx₃=30- qx₃ – линейное уравнение, т.е. N_5-5=30кН, N_6-6=30-40×4=-130кН. В пределах третьего грузового участка внутреннее усилие меняет знак, найдем расстояние от заделки до сечения, в котором N=0: x₃=130/40=3,25м (при этом значении x функция перемещений u имеет экстремум).

Все необходимые для построения эпюр внутренних усилий вычисления выполнены. При построении эпюры N необходимо соблюдать некоторые правила. Если на расчетной схеме приложена сосредоточенная сила (опорная реакция), то на эпюре соответственно в этом сечении будет скачек равный величине этой силы. Грузовому участку, в пределах которого действует равномерно распределенная нагрузка, на эпюре N соответствует участок с наклонной прямой (прямолинейная зависимость).