4. Расчет гидравлического удара с учетом закона закрытия затвора

Самым эффективным способом борьбы с гидравлическим ударом является подбор такого закона закрытия затвора, при котором повышение давления при гидравлическом ударе не приведет к разрушению материала трубы.

При закрытии затвора происходит сложный нестационарный процесс, при котором наблюдается наложение прямой и обратной волн повышенного давления.

В курсовой работе рассматриваются три варианта закрытия затвора. Для каждого варианта строится график изменения давления у затвора и определяется величина максимального давления при постепенном закрытии.

Определяется толщина стенок водовода по приведенным выше формулам для каждого варианта закрытия затвора. Из полученных значений принимается максимальная толщина стенок водовода.

Порядок расчета:

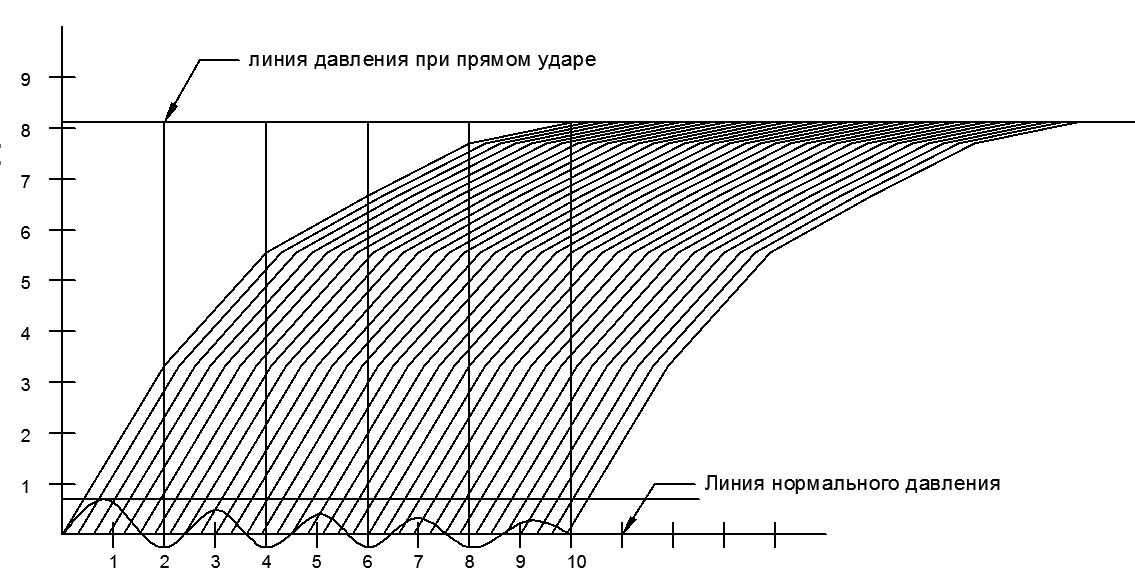
Строится график изменения скорости в зависимости от времени V = f(t): 1 - изменение скорости по линейному закону; 2 – изменение скорости по нелинейному закону (благоприятное); 3 – изменение скорости по нелинейному закону (менее благоприятное).

Если t_ф < T_з то волна понижения давления возникает у затвора раньше, чем последний будет закрыт, т.е. удар будет непрямым. Поэтому увеличение давления в водоводе не достигнет величины ΔР = Р_уд - Р₀ = ρС_удV₀ = 12,83 МПа.

Поскольку скорость изменяется по зависимости v=f(t), то повышение давления у задвижки в момент времени t определяется по зависимости

ΔP_t=ρ∙C_уд(V₀–V_t), Па, [1.23]

где V₀ определена выше;

Далее строится график зависимости V=f(t).

Для линейной зависимости V=f(t) с ее графика снимаются значения скоростей V_t в различные моменты времени и рассчитываются величины изменения давления ΔP_t.

Рассчитаем таким же образом ΔP_t при наилучшей (нижней) и наихудшей (верхней) зависимостях, сняв значения скоростей V_t с графика функции V = f(t).

Для каждой зависимости за промежуток времени от t = 0 до t = T_з = 10 с изменение давления будет выражено ломаной линией OABCDE, в координатах P-t

2 СЛУЧАЙ
t c	Vt	∆Pt
0	6,5	0
2	4,0	3,0
4	2,2	5,2
6	1,0	6,0
8	0,2	7,6
10	0	12,83

1 СЛУЧАЙ
t c	Vt	∆Pt
0	6,5	0
2	4,0	3,0
4	2,2	5,2
6	1,0	6,0
8	0,2	7,6
10	0	12,83

3 СЛУЧАЙ
t c	Vt	∆Pt
0	6,5	0
2	4,0	3,0
4	2,2	5,2
6	1,0	6,0
8	0,2	7,6
10	0	12,83

2. Волновое явление в открытых деривационных каналах гэс

2.1. Определение наибольших отметок уровней воды в деривационном канале при внезапном уменьшении нагрузки (расхода гэс)

Рассматривается приближенный расчет, поэтому наличием холостого сброса в виде быстротока пренебрегается. Рассматривается переходный процесс (от одного стационарного режима к другому), начинающийся при равномерном движении водного потока, которое соответствует режиму Q₀=0,8(Q_ГЭС)_max и характеризуется нормальной глубиной h₀. Таким образом, рассматривается один из частных случаев изменения расхода в сечении О–О.

При внезапном уменьшении расхода от Q₀=0,8(Q_ГЭС)_max =152м³/с до Q₀'=0,4(Q_ГЭС)_max = 76 м³/с их разность ΔQ=Q₀–Q₀' = 76 м³/с идет на пополнение деривационного канала. Первоначально возникшее в сечении О–О возмущение распространяется от напорного бассейна до водохранилища (сечения L–L) с некоторой скоростью, так называемой обратной положительной волны перемещения.

Увеличение уровня свободной поверхности в напорном бассейне в сечении О–О начинается (в рассматриваемом случае) от отметки ₀, соответствующей равномерному движению в канале, и продолжает увеличиваться в течение промежутка времени, за который обратная положительная волна при перемещении достигнет водохранилища в сечении L–L, отразится и в виде прямой положительной волны достигнет вновь сечения O–O, то есть напорного бассейна. Этому моменту и отвечает максимальная отметка (₀)_max уровня воды в напорном бассейне. Скорость распространения обратной и прямой волн перемещения одинаковая.

Расчет ведется по двум створам: O–O (створ ГЭС) и L –L (головное сечение деривационного канала). Отметка (₀)_max рассчитывается по следующей зависимости:

(₀)_max=₀''+(₀''–₀–ζ₀), м Б.С. [2.1]

где (₀)_max– искомая наибольшая отметка в створе О–О (створе ГЭС);

₀'' – отметка горизонта воды в створе О–О в тот момент времени, когда возникшая у ГЭС волна добежит до створа L–L (пройдет всю длину канала от ГЭС до головы);

₀=Пор – отметка горизонта воды в створе О–О в начальный момент времени, то есть тогда, когда происходит внезапное изменение расхода ГЭС (сброс нагрузки).

₀=Пор +i₀∙L_д+ ζ_L, м Б.С., [2.2]

ζ₀ – высота волны в створе О–О в начальный расчетный момент, то есть в момент внезапного изменения расхода.

₀ считается заданной, а ₀'', (₀)_max, ζ₀ и ζ_L (высота волны в сечении L–L в момент достижения его обратной положительной волны, то есть в момент добегания этой волны) должны вычисляться.

Необходимо вычислить высоту волны ζ₀ и скорость ее распространения C₀ для створа О–О в момент возникновения этой волны (в момент уменьшения расхода). Для этого решается совместно два уравнения (2.3) и (2.4) вида

ΔQ=Q₀–Q₀'=C₀∙B₀'∙ζ₀, м³/с, [2.3]

, м/с, [2.4]

где ω₀ – площадь поперечного сечения русла деривационного канала в начальный момент времени, определяется по формуле

ω₀=(b+m∙h₀)∙h₀ = (30+2×2,27)2,27 = 105,6 м², [2.5]

где b – ширина деривационного канала по низу, b=b_д=42 м);

m – коэффициент заложения откосов деривационного канала, m=m_д=2);

h₀ – глубина потока в головном сечении деривационного канала (L–L), h₀=h_н=2,27 м;

B₀' – ширина деривационного канала в сечении О–О по верху при глубине наполнения, равной 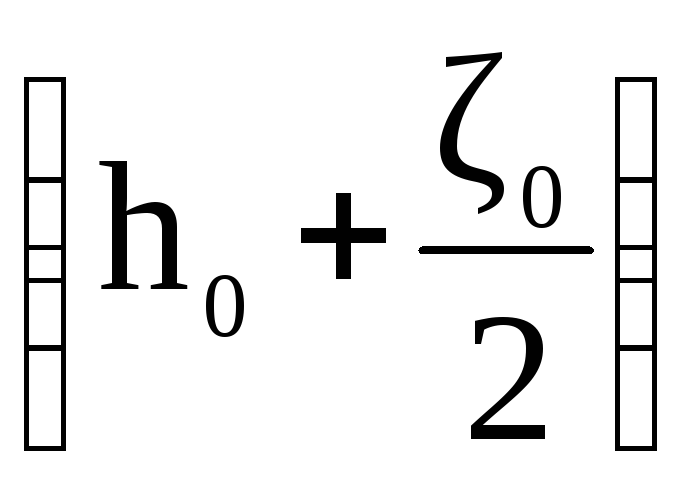м,

, м; [2.6]

V₀ – скорость установившегося движения потока при расходе в канале, равном Q₀, то есть до начала переходного процесса,

, м/с. [2.7]

Решение проведем графоаналитически, задавшись для этого рядом значений высоты волны ζ₀ и вычислив C₀ по формуле [2.4]. Затем подставив полученное значение C₀ в формулу [2.3], вычисляется ΔQ и строится график зависимости ΔQ=f(ζ₀), из которого находится искомое значение высоты волны , соответствующее величине ΔQ=Q₀–Q₀'=190-76 = 76м³/с (график 2.1).

Расчет сведен в таблицу 2.1.

V₀ = 176/105,6 = 1,7 м/с.

Таблица 2.1 – Определение высоты волны ζ₀ в створе О–О

ζ0	Bo	Co	ΔQ
0,1	51,3	3,0	15,4
0,2	51,5	3,1	32,0
0,3	51,7	3,2	50,2
0,4	51,9	3,3	68,5
0,5	51,1	3,5	89,4

=0,44 м.

В'₀ = 42 + 2×2(2,27 + 0,44/2) = 52 м.

С₀^исх = √9,81×105,6/52(1+3×52/2×105,6 ×0,44) – 1,7 = 3,4 м/с.

Далее вычисляется значение высоты волны ζ_L для створа L–L, то есть высота, которую волна приобретает, добегая до головного створа L–L.

Задавшись произвольными значениями ζ_L в пределах 1 м, последовательно находим:

а) площадь поперечного сечения волны в створе О–О Ω₀ по формуле

, м², [2.8]

где B₀ – ширина канала по верху в створе О–О,

B₀=b+2m∙h₀ = 42+2×2×2,27 = 51 м; [2.9]

ΔH – общее падение свободной поверхности канала до возникновения волны, то есть разность отметок свободной поверхности у головы канала и у ГЭС в начальный момент времени,

ΔH=i₀∙L_д0,00025×3000 = 0,75 м. [2.10]

б) площадь поперечного сечения волны в створе L–L Ω_L по формуле

Ω_L=(B_L+m∙ζ_L)∙ζ_L, м², [2.11]

где B_L=B₀.

в) объем призмы наполнения в канале, рассчитывающийся по зависимости

, м³/с. [2.12]

г) скорость волны в створе L–L, которая вычисляется параллельно по двум формулам

, м/c, [2.13]

, м/с, [2.14]

где ω_L=ω₀, v_L=v₀, а B_L' определяется по формуле

, м. [2.15]

Далее строятся графики зависимостей и. Точка их пересечения и является искомым значением высоты волны ζ_L.

B₀=42+2∙2∙2,27=51 м.

ΔH=0,00025∙3000=0,75м.

B_L=B₀=51 м.

V_L=V₀=1,7 м/с.

=0, 125м.

Определяем отметку ₀'' по формуле

, м Б.С. [2.16]

₀''=277,25 +0,75+0,125 = 278,125 м Б.С.

Тогда (₀)_max=2∙₀''–₀–ζ₀=2∙278,125–277,25–0,44 = 278,56 м Б.С.