
Математика
.pdf
Заметим, что если в тройке некомпланарных векторов a , b , c переставить два вектора, то она изменит свою ориентацию, т. е. из правой сделается левой или наоборот.
В дальнейшем правую тройку мы будем считать стандартной.
Определение. Под векторным произведением двух векторов a и b
понимается вектор c = a × b = [a, b],
для которого:
1) модуль равен, площади параллелограмма, построенного на данных векторах, т. е.
c = c = ab sin ϕ
где ϕ = (a, b) (0 ≤ ϕ ≤ π ) (рис. 2);
2) этот вектор перпендикулярен перемножаемым векторам (иначе говоря, перпендикулярен плоскости построенного на них параллелограмма), т. е.
c a и c b ;
3) если векторы неколлинеарны, то векторы a , b , c образуют правую тройку векторов.
Укажем основные свойства векторного произведения.
1) При изменений порядка сомножителей векторное произведение меняет свой знак на обратный, сохраняя модуль, т. е.
b × a = −(a × b).
Действительно, при перестановке векторов a и b площадь пост-
роенного на них параллелограмма остается неизменной, т. е. b × a
= a × b . Однако тройка векторов b, a, a× b является левой.
Поэтому |
направление вектора |
b |
× |
a |
|
|
противоположно направлению |
||||||
|
|
× |
|
|
|
|
|
|
|
||||
вектора |
a |
b |
|
(а и b неколлинеарны). Если a и b коллинеарны, то равенство |
|||||||||
очевидно.
Таким образом, векторное произведение двух векторов не обладает
переместительным свойством.
2) Векторный квадрат равен нуль-вектору, т. е. a × a = 0.
Это — очевидное следствие свойства 1).
51
3) Скалярный множитель можно выносить за знак векторного произведения, т. е. если λ — скаляр, то
(λ a × b)= (a × λb)= λ (a × b).
Это свойство |
|
непосредственно |
вытекает из смысла произведения вектора |
||||||||||||||||||
на скаляр и определения векторного произведения. |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4) Для любых |
трех векторов a , b , c справедливо равенство |
||||||||||||||||||||
( |
|
+ |
|
)× |
|
= ( |
|
× |
|
)+ ( |
|
+ |
|
) |
|
|
|
|
|||
a |
b |
c |
a |
c |
b |
c |
|
|
|
|
|||||||||||
т. е. векторное произведение |
|
обладает распределительным |
|||||||||||||||||||
свойством. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
С помощью векторного произведения удобно формулировать легко проверяемое необходимое и достаточное условие коллинеарности двух
векторов a и b : a × b = 0 .
§ 3. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ В КООРДИНАТНОЙ ФОРМЕ Пусть
a = ax i + ay j + az k
и
b = bx i + by j + bz k
Перемножая векторно эти равенства и используя свойства векторного произведения, получим сумму девяти слагаемых
|
|
× |
|
= [ax bx ( |
|
× |
|
)+ ay bx ( |
|
× |
|
)+ az bx ( |
|
× |
|
)]+ |
|||||||||||||||||||||||||
a |
b |
i |
i |
j |
i |
k |
i |
||||||||||||||||||||||||||||||||||
[ax by |
( |
|
|
× |
|
|
|
)+ ay by |
( |
|
|
× |
|
|
|
)+ az by |
( |
|
|
× |
|
)]+ |
|||||||||||||||||||
i |
j |
j |
j |
k |
j |
||||||||||||||||||||||||||||||||||||
[ax bz |
( |
|
× |
|
)+ ay bz |
( |
|
× |
|
)+ az bz |
( |
|
+ |
|
)] |
||||||||||||||||||||||||||
i |
k |
j |
k |
k |
k |
||||||||||||||||||||||||||||||||||||
Из определения векторного произведения и его свойств следует, что для
ортов i , |
j , k справедлива следующая «таблица умножения»: |
|||||||||||
|
|
× |
|
= 0 , |
|
× |
|
= 0 , |
|
× |
|
= 0 |
i |
i |
j |
j |
k |
k |
|||||||
i × j = −(j × i)= k j × k = −(k × j)= i k × i = −(i × k )= j
52

Поэтому получаем
ab = i(ay bz − az by )+ j(az bx − ax bz ) + k(ax by − ay bx )=
|
|
ay |
az |
- |
|
|
ax |
az |
+ |
|
|
ax |
ay |
i |
|
j |
k |
||||||||||
|
|
by |
bz |
|
|
|
bx |
bz |
|
|
|
bx |
by |
§ 4. СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Определение. Под смешанным (или векторно-скалярным) произведением
векторов a , b и c понимается число abc = (a × b)c
Построим параллелепипед П (рис. 1), ребрами которого, исходящими из
общей вершины О, являются векторы a , b , и c .
Тогда |
a |
× |
b |
|
= S представляет |
|
собой |
площадь параллелограмма, |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
построенного на векторах a и b , т. е. |
есть |
площадь основания |
||||||||||||||||||||||||
параллелепипеда. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Высота |
|
|
|
этого |
параллелепипеда |
H, |
очевидно, |
|
|
равна |
||||||||||||||||
Н=± npsc = ± с cosϕ , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
где |
|
= |
|
× |
|
и знак плюс соответствует острому углу ϕ = (c, S) , |
|
|
|
|
||||||||||||||||
S |
a |
b |
|
а |
|
знак |
||||||||||||||||||||
минус — тупому углу ϕ . |
В первом |
|
случае векторы а, b, с |
|
|
|
|
|||||||||||||||||||
S образуют |
правую тройку, |
а во втором — левую тройку. |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
П |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Тогда на основании определения скалярного произведения имеем |
|
|
|
|
||||||||||||||||||||||
|
|
с |
|
|
|
|
|
|
|
|
|
(a b)c = Sc=S прSс=±SH=±V, |
где V |
|||||||||||||
H |
|
|
|
|
|
|
|
|
|
|
—объем |
|
параллелепипеда, |
|||||||||||||
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
построенного на векторах a , b , |
c . |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
O |
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Рис.1
53

Отсюда
abc = ±V ,
т. е. смешанное произведение трех векторов равно объему V параллелепипеда, построенного на этих векторах, взятому со знаком плюс, если эти векторы образуют правую тройку, и со знаком минус, если они образуют левую тройку.
Справедливы следующие основные свойства смешанного произведения.
1) Смешанное произведение не меняется при циклической перестановке его сомножителей, т. е.
abc = bca = cab
Действительно, в этом случае не изменяется ни объем параллелепипеда П, ни ориентация его ребер.
2) При перестановке двух соседних множителей смешанное произведение меняет свой знак на обратный, т. е.
bac = acb = cba = −abc .
Это следует из того, что перестановка соседних множителей, сохраняя объем параллелепипеда, изменяет ориентацию тройки векторов, т. е. правая тройка переходит в левую, а левая — в правую.
С помощью смешанного произведения получаем необходимое и достаточное условие компланарности трех векторов a , b , c :
abc = 0
54
Лекция 12
ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ НА ПЛОСКОСТИ
Аналитическая геометрия – раздел математики, в котором геометрические задачи решаются средствами алгебры на основе метода координат и введения произвольной (переменной) точки объекта, предложенных Декартом.
§1. ЛИНИИ НА ПЛОСКОСТИ
Прямая
Рассмотрим несколько уравнений с двумя неизвестными: 1) y − 2x + 1 = 0, 2) y = x2 − 1, 3) x2 + y2 = 0, 4) x2 + y2 = −1. Уравнениям 1) и 2) отвечают линии (прямая и парабола), уравнению 3) отвечает лишь одна точка, а 4) – ни одна точка. Условимся, что в случае 3) соответствующая линия вырождается в точку (в данном случае - окружность нулевого радиуса), а уравнению 4) – мнимая линия (в данном случае – мнимая окружность). Отсюда делаем вывод: между множеством действительных или мнимых линий плоскости и множеством уравнений с двумя неизвестными существует взаимооднозначное соответствие.
Определение. Выражение F(x, y) = 0 называется уравнением данной линии, если ему удовлетворяют все точки, лежащие на данной линии и не удовлетворяет ни одна точка, не принадлежащая данной линии.
Простейшей в определенном смысле является прямая. Ориентацию
прямой L на |
плоскости |
можно задать с помощью нормального вектора |
|
(произвольного |
вектора, |
перпендикулярного L ). При этом такую же |
|
ориентацию имеет множество прямых, параллельных |
L . Чтобы из этого |
||
множества выделить L , |
необходимо указать точку |
M 0 L. Так что |
|
нормальный вектор и точка определяют конкретную прямую и наоборот, для произвольной прямой можно указать хотя бы одну точку, через которую она проходит, и нормальный вектор этой прямой. Эти соображения существенно используются при доказательстве основной теоремы о прямой на плоскости. Между множеством всех прямых плоскости и множеством всех уравнений первой степени с двумя неизвестными существует взаимно однозначное соответствие.
55

|
|
|
|
= |
(A, B) L , |
M 0 (x0 , y0 ) L . |
|
|
Пусть |
n |
Возьмем на |
||||||
прямой |
|
L |
точку M (x, y) и построим |
вектор |
||||
|
|
= (x − x0 , y − y0 ) |
(рис. 1). Утверждение |
|||||
|
M 0 M |
|||||||
«задана |
|
|
прямая» |
означает, |
что |
M L . |
||
Воспользуемся |
определением |
|||||||
перпендикулярности векторов
Рис.1
(M L) (M 0 M n) (n M 0 M = 0) (A(x − x0 ) + B( y − y0 ) = 0)
(Ax + By + (− Ax0 |
|
Ax + By |
+ C = |
0 |
|
− By0 ) = 0) |
|
|
− By |
|
|
|
|
C = − Ax |
0 |
|
|
|
|
|
|
0 |
|
Уравнение Ax + By + C = 0
называется общим уравнением прямой на плоскости. Исследуем данные уравнения:
1) |
при C = 0 уравнение имеет вид |
Ax + By = 0 |
и O(0,0) L , т.е. L |
||||||||||
проходит через начало координат; |
|
|
|
|
|||||||||
2) |
при B = 0 , |
|
|
= (A.0) OY и |
L OY , а уравнение принимает вид |
||||||||
n |
|||||||||||||
Ax + C = 0 или x = − |
C |
; обозначим |
− |
C |
= x0 , тогда |
x = x0 – уравнение |
|||||||
|
A |
||||||||||||
|
|
|
|
|
|
|
A |
|
|
|
|||
прямой, параллельной оси OY ; |
|
|
|
|
|||||||||
|
3)при B = 0 и C = 0 имеем X = 0 – уравнения оси OY . Если A = 0 или |
||||||||||||
A = 0 и C = 0 , то имеем случаи пп. 2) и 3). |
|
|
|||||||||||
Пусть в уравнении B ≠ 0 , тогда, разделив его на B , получим |
|||||||||||||
y = − |
A |
x − |
C |
|
|
|
|
|
|||||
|
B |
|
|
|
|
||||||||
|
B |
|
|
|
y = kx + b , находим |
||||||||
Сравнивая это выражение с уравнением |
|||||||||||||
−A = k , − C = b . B B
Рассмотрим другие виды уравнений прямой.
Определение. Пучком прямых с центром в данной точке называется множество всех прямых плоскости, проходящих через эту точку.
Рис. 2 |
Рис. 3 |
56
Пусть M 0 (x0 , y0 ) – центр пучка (рис. 2). Тогда уравнение произвольной
прямой данного пучка имеет вид
A(x − x0 )+ B(y − y0 ) = 0
Если B ≠ 0 (L ⁄ OY), то y − y0 = − A (x − x0 ) или
B
y − y0 = k(x − x0 )
Если B ≠ 0 , то x − x0 = 0 или x = x0
Совокупность уравнений
y − y0 |
= k(x − x0 ) |
|
|
x = x0 |
|
называют уравнениями пучка прямых.
Пусть теперь M (x, y) L – произвольная точка L . Составим уравнение L , для чего построим векторы M1M 2 = (x2 − x1 , y2 − y1 ) и M1 M = (x − x1 , y − y1 ) . Точка M L тогда и только тогда, когда MM1 M 2 M1 , т.е. когда (рис. 3)
x − x1 |
= |
y − y1 |
x2 − x1 |
y2 − y1 |
|
Это и есть искомое уравнение, поскольку оно связывает координаты произвольной точки L и заданные числа.
В случае прямых, параллельных координатным осям (нуль в знаменателе), мы все-таки получаем уравнение прямой, полученной в виде . Для этого следует воспользоваться основным свойством пропорции.
Рис. 4 |
|
|
Рис. 5 |
|
|
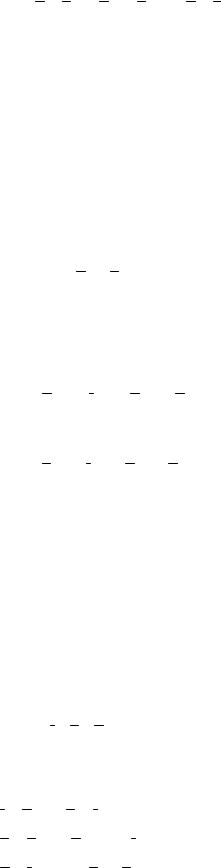
Пусть прямая L отсекает от координатных осей OX и OY отрезки длиной |
|||||
a и |
b соответственно (рис.4). Очевидно, что M1 |
(a,0) = L ∩ OX , |
|||
M 2 (0,b) = L ∩ OY . |
|
||||
Тогда, получаем |
|
||||
|
x |
+ |
y |
= 1 |
|
|
a |
|
|
||
|
|
b |
|
||
Это – уравнение прямой в отрезках.
Рассмотрим взаимное размещение двух прямых (рис. 5).
57

Пусть имеем |
две прямые |
y = k1 x + b1 (L1 ), |
|
y = k2 x + b2 (L2 ). Очевидно |
|||||||||||
0 ≤ (L , L |
) < π . Так как k |
1 |
= tgα |
, k |
2 |
= tgα |
2 |
,α |
2 |
= α |
1 |
+ ϕ , то |
|||
1 € 2 |
|
|
|
1 |
|
|
|
|
|
|
|||||
tgϕ = tg(α 2 |
− α1 ) = |
tgα 2 − tgα1 |
= |
k2 − k1 |
|
|
|
||||||||
|
|
|
|
|
|||||||||||
|
|
1+ tgα1tgα 2 |
1+ k1k2 |
|
|
|
|||||||||
Для параллельных и перпендикулярных прямых tgϕ = 0 , tgϕ = π , т.е. 2
k1 − k2 = 0 и 1+ k1k2 = 0 соответственно. Отсюда, условия параллельности и перпендикулярности прямых соответственно выглядят так
k1 = k2 , k2 = − 1 k1
§2. КРИВЫЕ ВТОРОГО ПОРЯДКА
Прямая – это алгебраическая линия первого порядка. Что касается алгебраических линий второго порядка, то к ним относятся окружность, эллипс, парабола и гипербола (не считая случаи их вырождения).
Общий вид уравнения линий второго порядка:
Ax2 + 2Bxy + Cy2 + 2Dx + 2Ey + F = 0
A,B,C,D,E,F R,
где хотя бы один из коэффициентов A, B,C отличен от нуля.
Окружность
Определение. Окружность – множество точек M плоскости, равноотстоящих от данной точки M 0 , называемой центром; d(M 0 , M ) – называется радиусом окружности.
Составим уравнение окружности, если даны M 0 (x0 ,y0 ), M (x, y),
MM 0 = R . Тогда имеем
(x − x0 )2 + (y − y0 )2 = R2
Если M 0 (0,0), то имеем каноническое уравнение окружности
x2 + y2 = R2 .
Раскрывая скобки, приведем уравнение к виду:
58
x2 + y2 − 2xx0 − 2yy0 + (x0 2 + y0 2 − R2 )= 0
Таким образом, признаки, по которым из общего уравнения линии второго порядка можно получить уравнение окружности, это A = C и B = 0 .
Эллипс
Определение. Эллипс – это множество точек плоскости, которое в некоторой прямоугольной системе координат удовлетворяет уравнению
x2 |
+ |
y2 |
= 1, a R,b R . |
|
a2 |
b2 |
|||
|
|
Это каноническое уравнение эллипса. Его форму можно установить способами дифференциального исчисления.
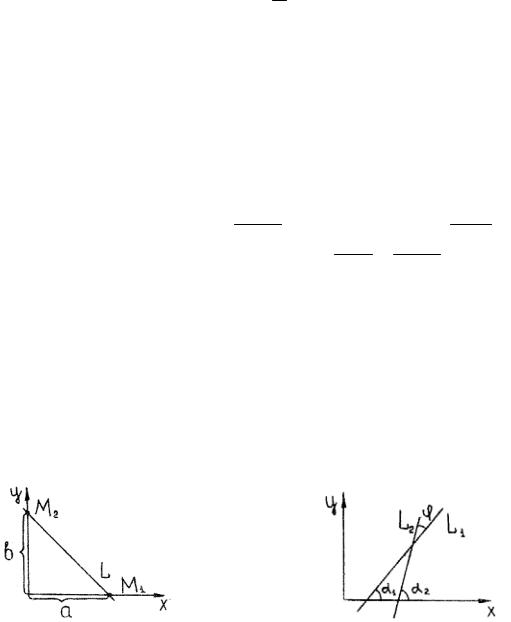
Основное геометрическое свойство эллипса заключается в том, что сумма расстояний от данной точки M до двух точек плоскости F1 и F2 , называемых фокусами, есть величина постоянная.
Пусть |
d(F1 , F2 ) = 2c, M (x, y) |
– |
переменная |
точка |
Рис.6 |
|
|||||
эллипса (рис.6), докажем, что |
|
|
|
|
|
||||||
d(M , F1 )+ d(M , F2 ) = 2a |
|
|
|
|
|
|
|
|
|||
|
Имеем |
|
|
|
|
|
|
|
|
||
|
|
d(M,F ) = (x − c)2 + y2 ,d(M, F ) = (x + c)2 + y2 |
|
|
|||||||
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
Подставляя эти выражения |
в доказываемую формулу и |
обозначая |
||||||||
a2 |
− c2 = b2 , получим |
x1 |
+ |
y2 |
|
= 1, |
a,b R |
|
|
|
|
a1 |
b2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||
|
Различают такие элементы эллипса (рис. 6): |
A1 , A2 , B1 , B2 – его вершины, |
|||||||||
O |
– |
центр, A1 A2 – большая и |
B1 B2 – малая оси, |
F1 F2 = 2c – |
фокусное |
||||||
расстояние, - эксцентриситет.
Величина эксцентриситета ε оценивает степень сплющенности эллипса.
Если a = b = R , то |
ε=0 – имеем окружность. При b = 0 ε=1 – отрезок |
прямой. Это случай |
вырождения эллипса. В общем случае 0<ε<1. |
Гипербола
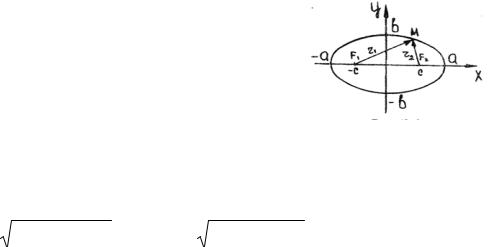
Определение гиперболы аналогично определению эллипса, ее каноническое уравнение имеет вид
x2 |
− |
y2 |
= 1,a > 0,b > 0 |
|
a2 |
b2 |
|||
|
|
В формулировке основного геометрического свойства гиперболы нужно слова «сумма» (в случае эллипса) заменить словом «модуль разности». Это
59
свойство можно проверить также, как и в случае эллипса, приняв во
внимание обозначение c2 = a2 + b2 (рис. 7). |
|
|
|
|
Различают такие элементы гиперболы: A1 , A2 |
– действительные и B1 , B2 – |
|||
мнимые |
вершины (гипербола не пересекает |
ось OY , |
при |
x = 0 имеем |
y2 = −b2 , |
A1 A2 – действительная и B1 B2 – мнимая оси, |
F1 F2 |
– фокусное |
|
расстояние, ε - эксцентриситет (ε = |
c |
), прямые |
y = ± |
b |
x называются |
|
|
||||
|
a |
|
a |
||
асимптотами. |
|
|
|
||
Рис.7 |
Рис.8 |
Определение. Асимптота данной кривой – это прямая, расстояние до которой от произвольной точки кривой стремится к нулю, когда указанная точка кривой стремится к бесконечности.
Парабола
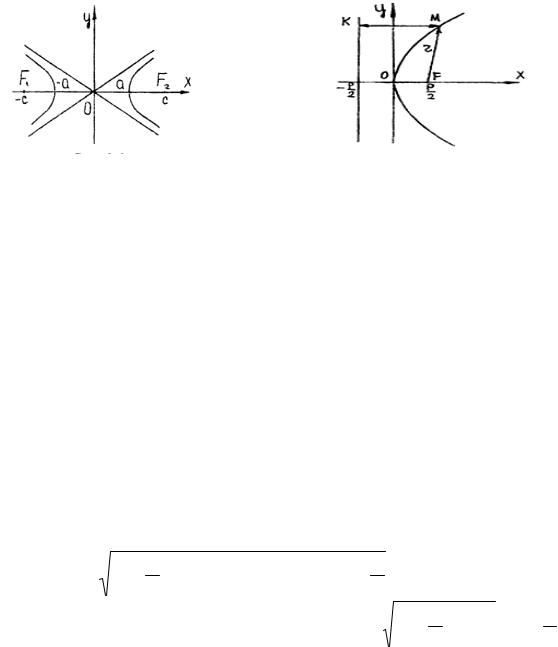
Определим параболу уравнениями
y2 = 2 px, x2 = 2 py, p R, q R.
Основное геометрическое свойство параболы то, что она представляет собой множество точек плоскости, равноотстоящих от некоторой точки, называемой фокусом, и некоторой прямой, называемой директрисой.
Действительно, пусть расстояние от |
фокуса до директрисы равно p |
|
(рис.8), а M (x, y) – произвольная точка параболы. Имеем |
|
|
MF = (x − p)2 + y 2 , d(MF) = MK = x + p |
|
|
2 |
2 |
|
Равенство MF = MK можно записать в виде (x − p)2 + y 2 |
= x + p , откуда |
|
|
2 |
2 |
y2 = 2 px .
Вырожденные случаи параболы имеем, когда ее ветви складываются в положительную (p>0) или отрицательную (p<0) части оси OX или разгибаются до оси OY .
60
